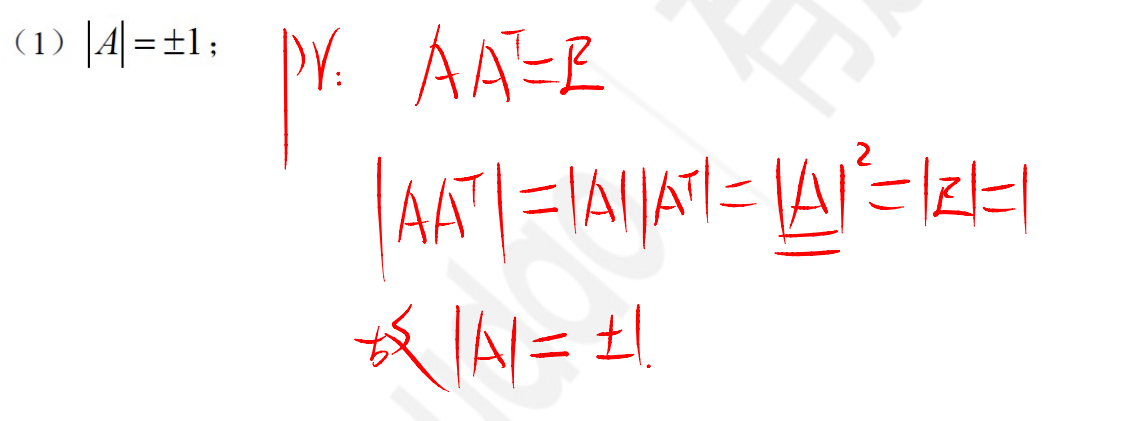线代基础

行列式

概念

全排列：n个数排成一列

标准排列：由小到大排列

逆序：排列中两个元素，大的数在小的数之前

逆序数：一个排列中所有逆序的总数

奇（偶）排列：逆序数为奇（偶）数

对换：在排列中，将任意两个元素对换

• 一个排列中的任意两个元素对换，排列改变奇偶性
• 奇排列对换成标准排列的对换次数为奇数，偶排列对换成标准排列的对换次数为偶数

三阶行列式：

n阶行列式：n!项不同行不同列元素乘积的代数和

上（下）三角形行列式：主对角线以下（上）都是0

对角线行列式：主对角线上下都是0

性质（化简行列式）

转置行列式：

性质1：行列式与它的转置行列式相等

性质2：对换行列式的两行（列），行列式变号

• 如果行列式有两行（列）完全相同，则此行列式等于零

性质3：行列式的某一行（列）中所有的元素都乘同一数 k，等于用数 k 乘此行列式

• 行列式中某一行（列）的所有元素的公因子可以提到行列式记号的外面

性质4：行列式中如果有两行（列）元素成比例，则此行列式等于零

性质5：

性质6：把行列式的某一行（列）的各元素乘同一数然后加到另一行（列）对 应的元素上去，行列式不变

典型题型

1. 化为上（下）三角

   

2. n阶ab型行列式

   

   结论

   

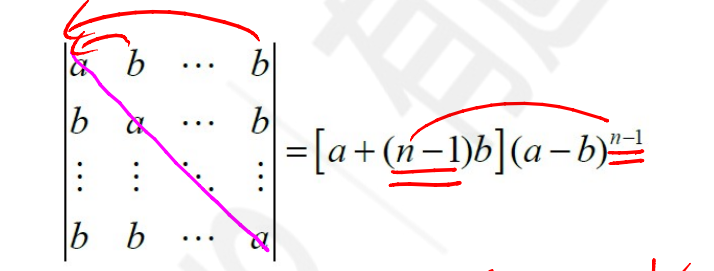
3. 拉普拉斯展开式

   设A为m阶矩阵，B为n阶矩阵

   

   

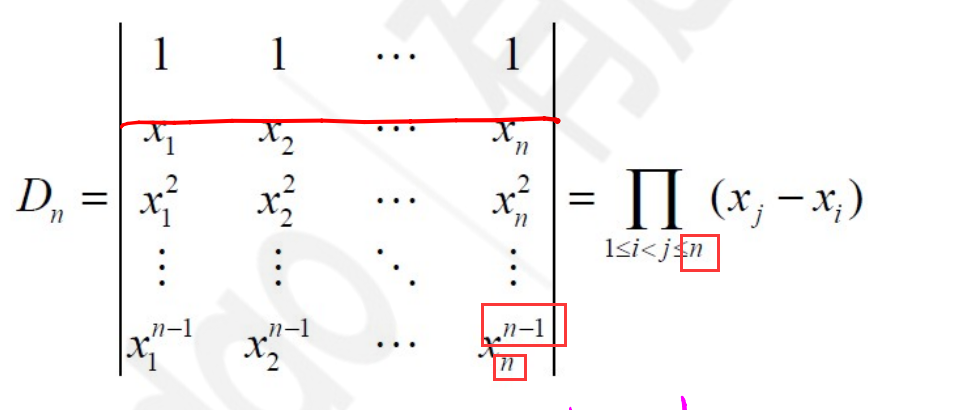
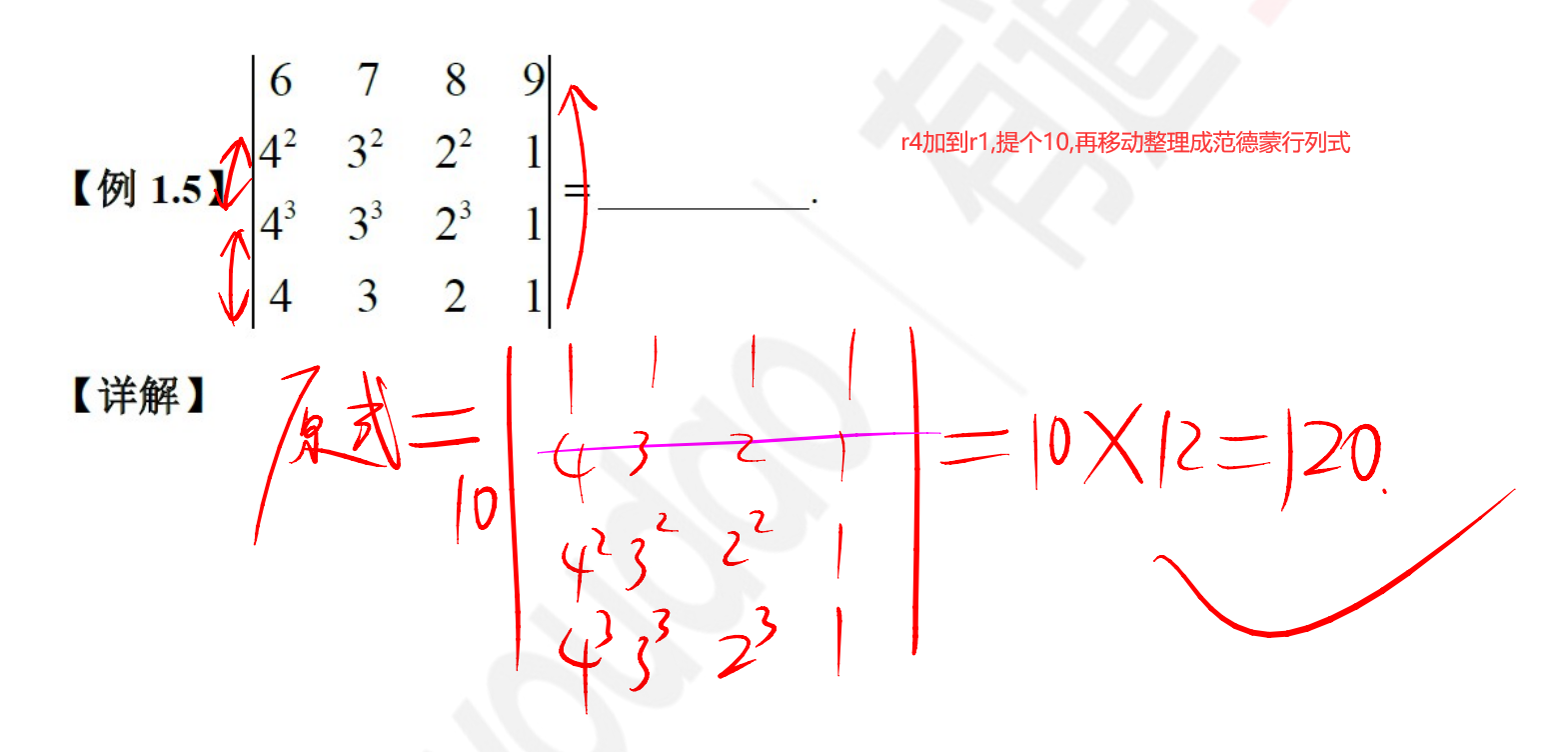
4. 范德蒙行列式

   由1阶、2阶、3阶…归纳法得出

   

   

   

行列式展开

概念

余子式：把i行和j列去掉后剩下的n-1阶行列式，记作M(i,j)

代数余子式：A(i,j) = (-1)^(i+j) M

行列式按行（列）展开法则

行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和

行列式某一行（列）的元素与另一行（列）的对应元素的代数余子式 乘积之和等于零

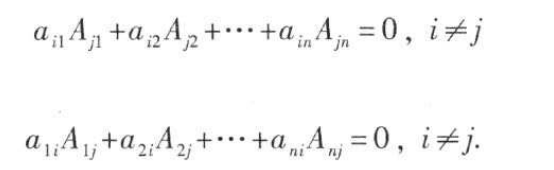
例题

例题1

有很多0，考虑用按行展开

例题2

余子式、代数余子式求和

行列式的公式

注意A、B为矩阵

公式1

公式2

乘积的行列式等于行列式的乘积

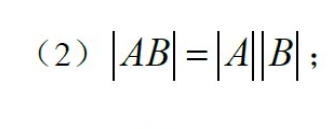
公式3

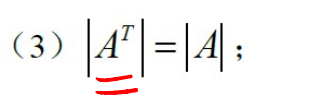
公式4

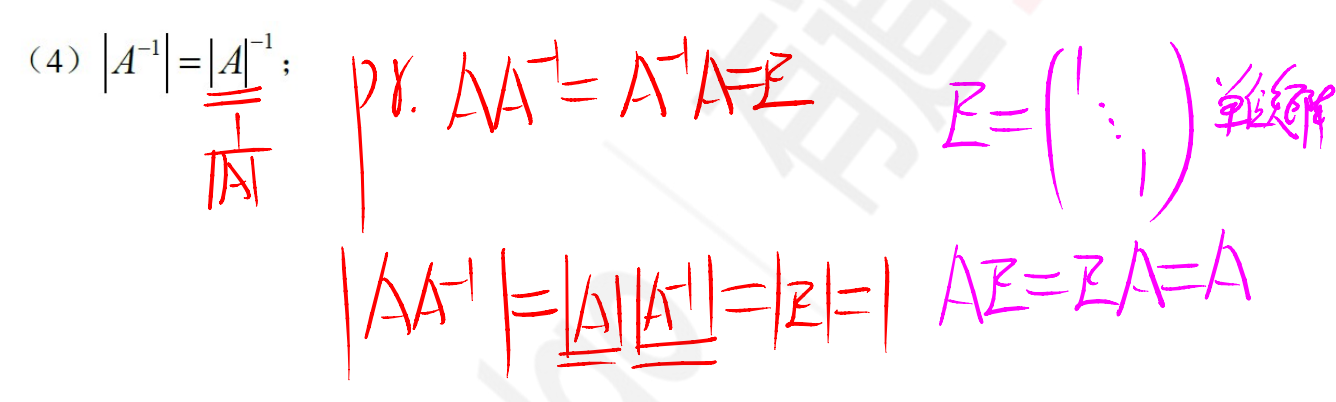
公式5

伴随矩阵

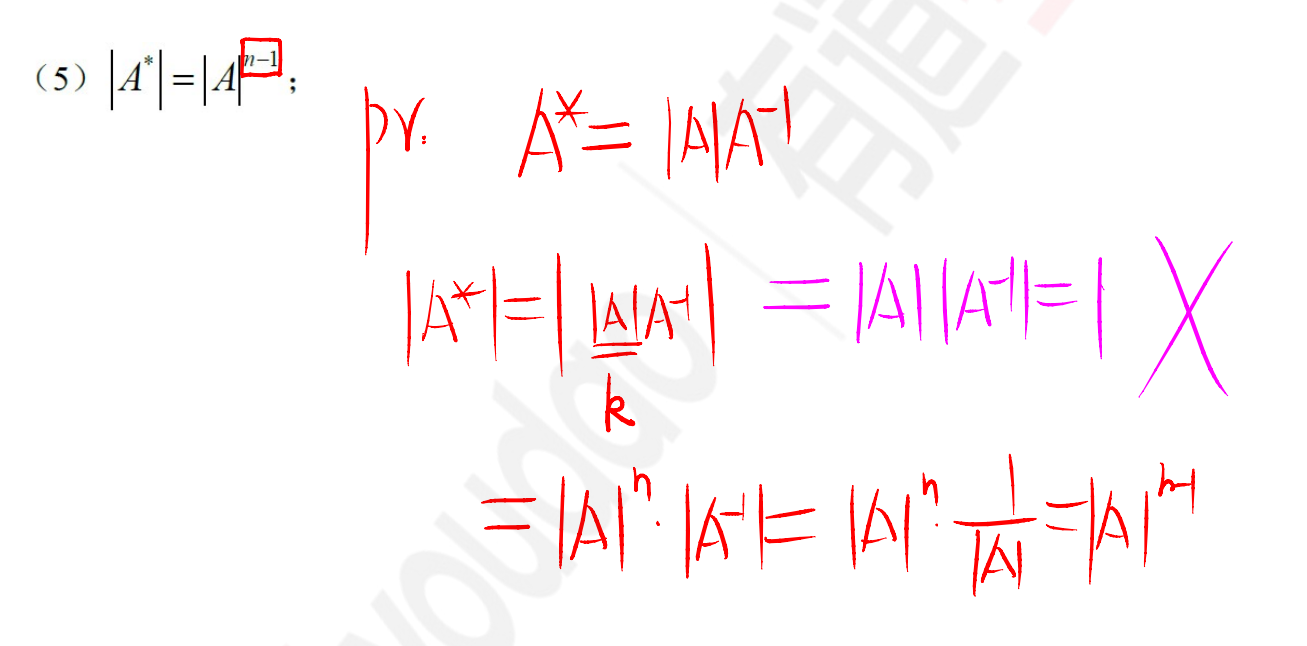
公式6

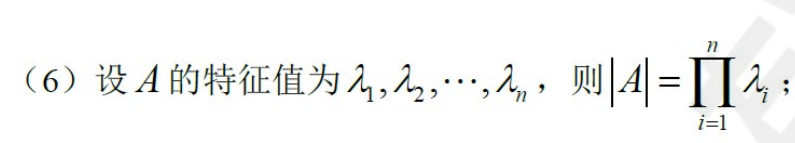
公式7

Cramer法则

矩阵

概念

n阶矩阵（n阶方阵）：行数与列数都等于n的矩阵

行（列）矩阵：只有一行（列）的矩阵

零矩阵：元素都是零的矩阵

单位矩阵：

矩阵乘法：

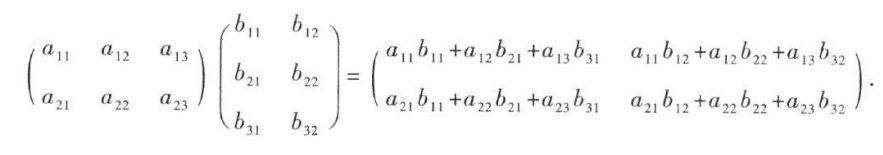
注意：

1. 只有当第一个矩阵（左矩阵）的列数等于第二个矩阵（右矩阵）的 行数时，两个矩阵才能相乘
2. 矩阵乘法不满足交换律，不满足因式分解
3. 矩阵的乘法中必须注意矩阵相乘的顺序

伴随矩阵：

各个元素的代数余子式 Aij所构成的矩阵

二阶的伴随矩阵为：主对角线互换，副对角线变号

性质：

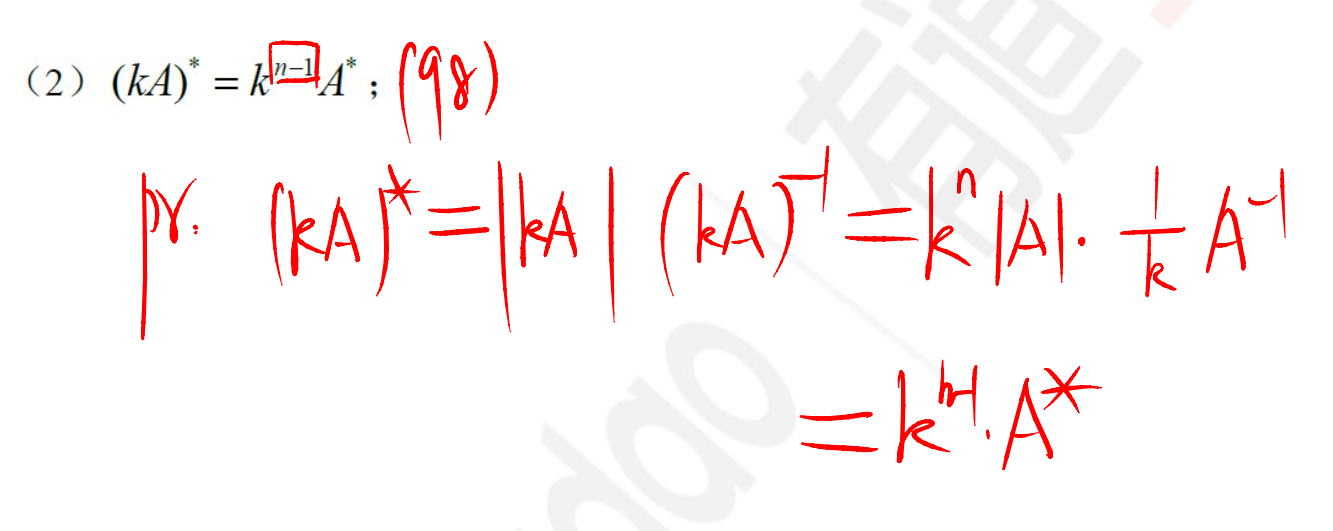
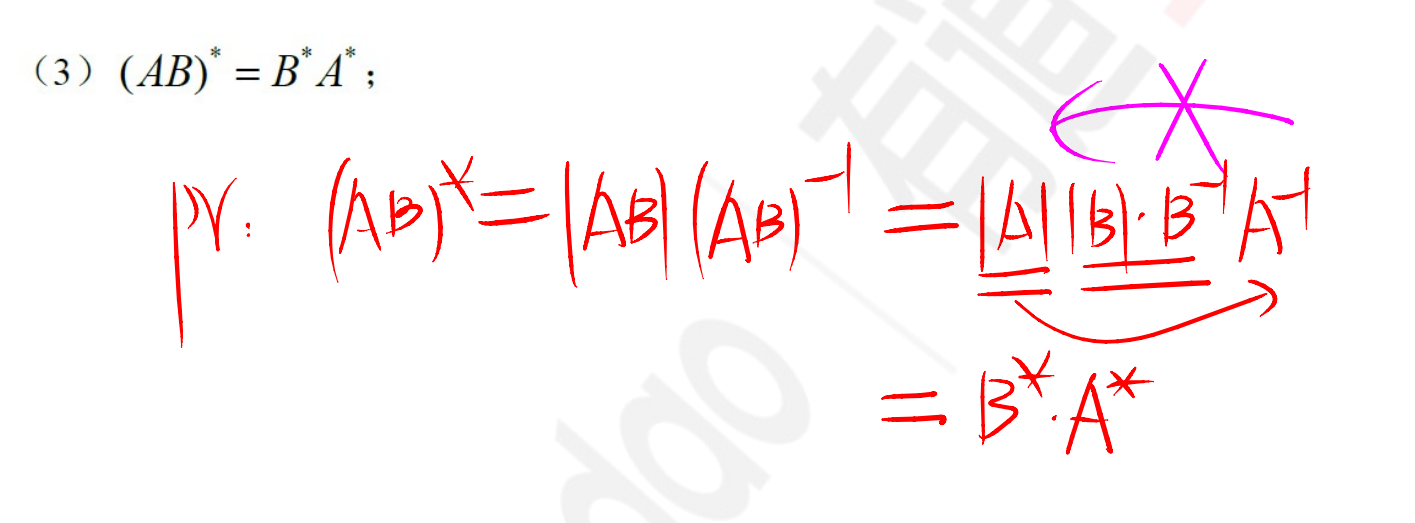
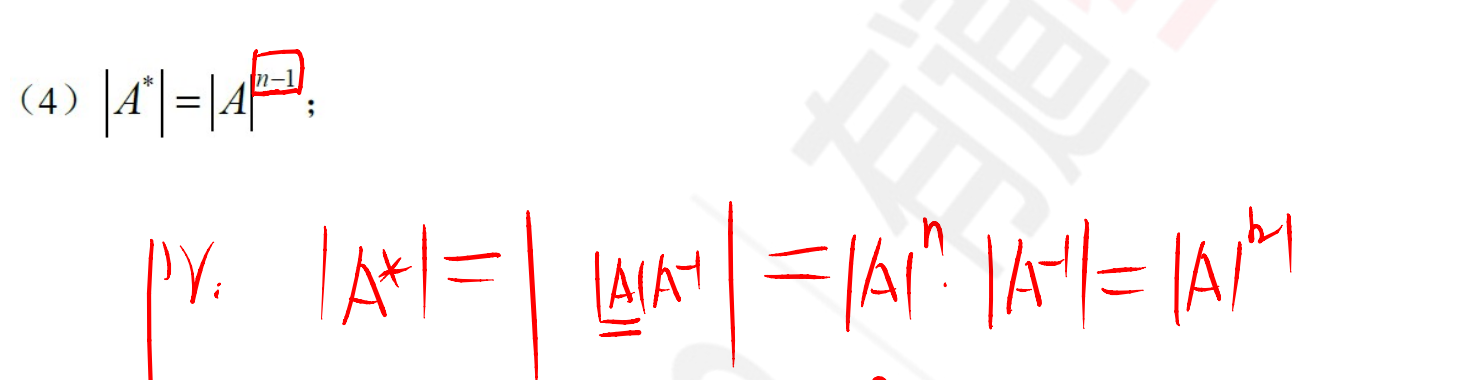
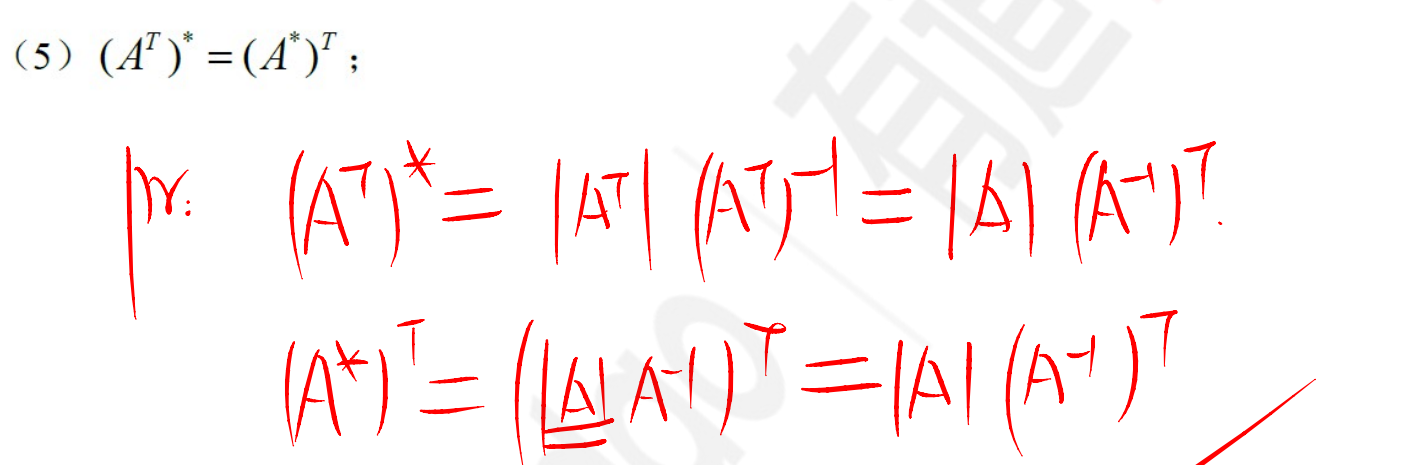
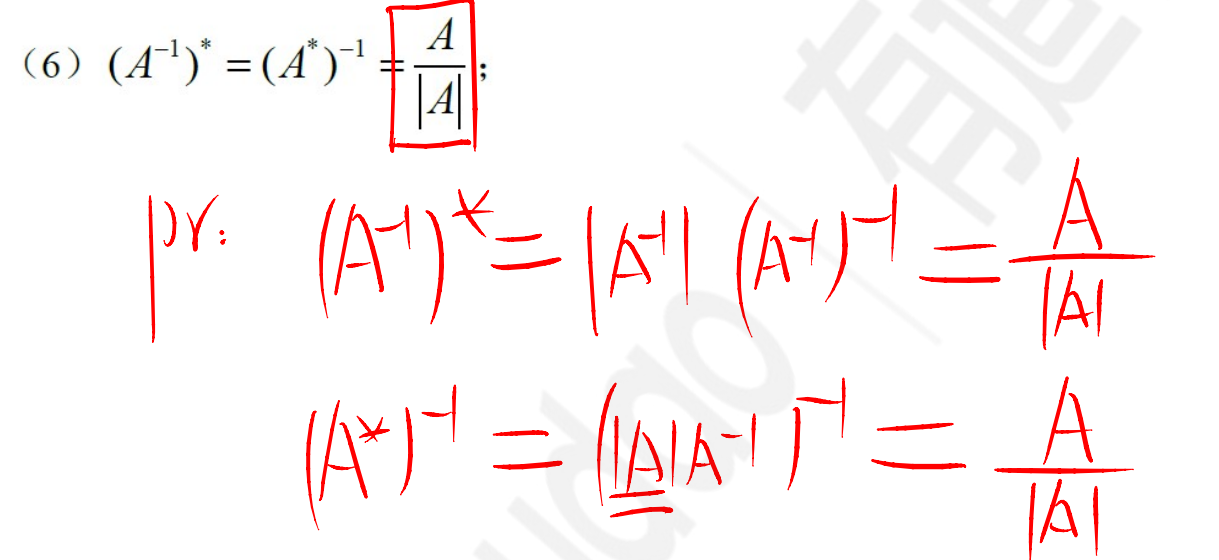
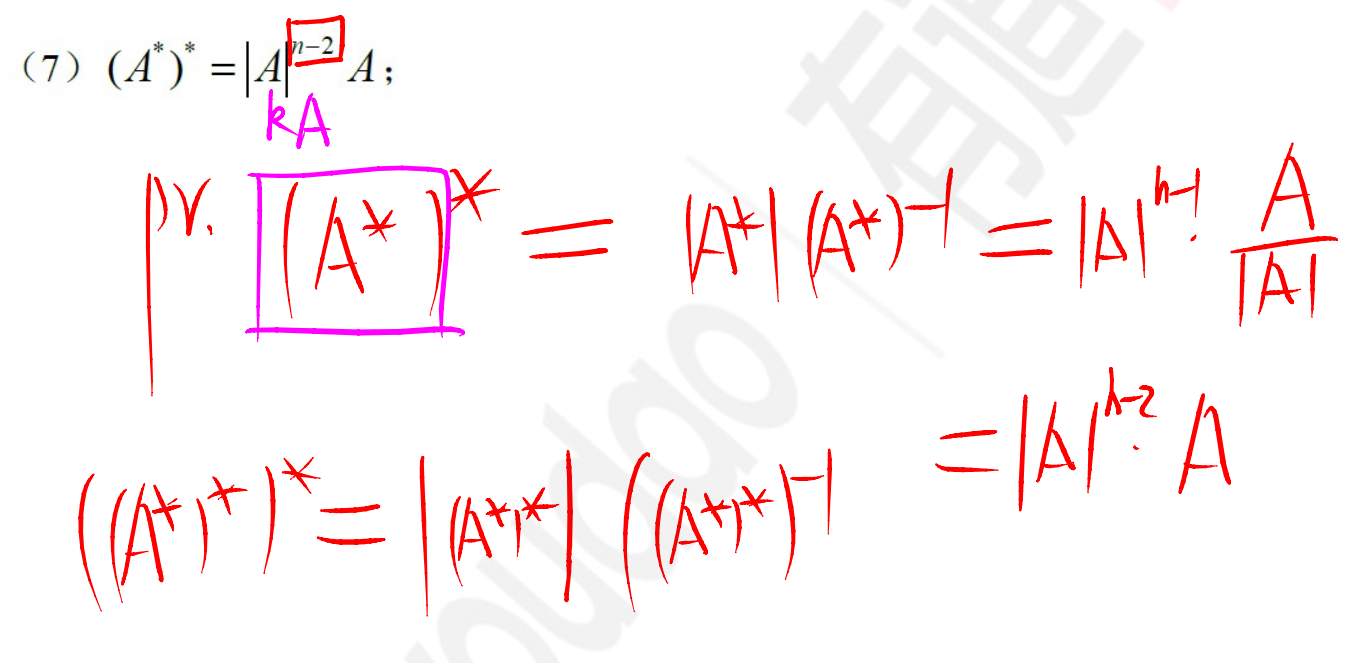
矩阵转置

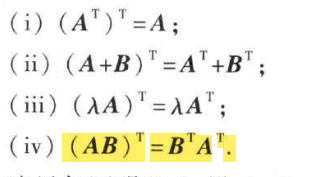
对称矩阵：A的转置=A

反对称矩阵：A的转置=-A

逆矩阵

如果有一个n阶矩阵B，使AB = BA = E，则矩阵A是可逆的

注意：

1. 如果矩阵 A 是可逆的，那么 A 的逆矩阵是惟一的
2. 可逆的矩阵一定是个方阵
3. 若|A| ≠ 0，则矩阵A可逆

可逆的充要条件：

1. |A|≠0
2. r(A)=n
3. 行（列）向量组线性无关
4. 齐次线性方程组Ax=0只有零解
5. 非齐次线性方程组Ax=b有唯一解
6. Ade特征值均不为零

性质：

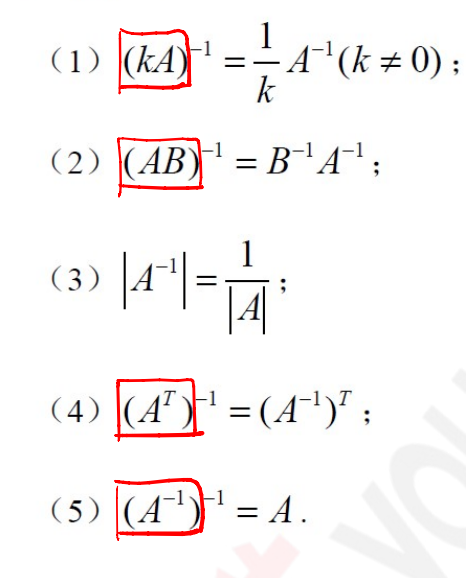
例题1：

逆的求法

1. 定义法：AB=E或BA=E

2. 初等变换法：

   

   

3. 伴随矩阵法：

   

初等变换

初等变换：

1. 对换两行（列）
2. 数k乘以某行（列）(k != 0)
3. 某行（列）* k加到另一行（列）

初等矩阵：

​ 单位矩阵E经过一次初等变换得到的矩阵

1. E(i, j)：i, j两行（列）互换
2. E(i(k))：i行乘以k
3. E(ij(k))：j行乘k加到i行（或i列乘k加到j列）

矩阵等价：

​ 矩阵A经有限次初等变换变成矩阵B，就称矩阵A与B等价，记作A~B

行阶梯形矩阵：

1. 非零行在零行的上面
2. 非零行的首非 零元所在列在上一行（如果存在的话）的首非零元所在列的右面

行最简形矩阵：

1. 非零行的首非零元为1
2. 首非零元的上下都是0

性质：

1. 设 A 是一个 m×n 矩阵，对 A 施行一次初等行变换，相当于在 A 的 左边乘相应的 m 阶初等矩阵；对 A 施行一次初等列变换，相当于在 A 的右边乘 相应的 n 阶初等矩阵
2. 

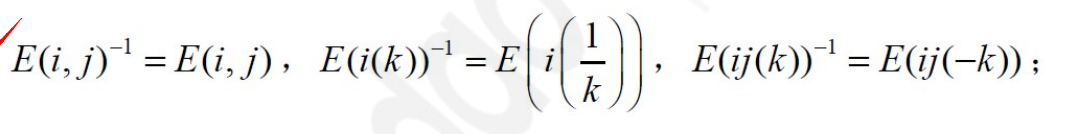
秩

概念

秩：非零子式的最高阶数

满秩矩阵：秩等于矩阵的阶数，可逆

降秩矩阵：秩小于矩阵的阶数，不可逆

性质

1. 0 ≤ R（A ）≤min{m，n}，A为m*n的矩阵
2. max {R(A), R(B)} ≤ R(A, B) ≤ R(A) + R(B)
3. R（A B）≤ min｛R（A），R（B）｝
4. R(A ^ T) = R(A)
5. 若A~B，则R(A) = R(B)
6. R(A+B) <= R(A)+R(B)
7. 若P、Q可逆，则R（PAQ）=R（A）
8. 若 A m×n Bn×l = O，则 R（A）+R（B） ≤　n
9. 矩阵乘法的消去律： A B = O，若 A 为列满秩矩阵，则 B = O

中文描述：秩小于等于行数和列数、和的秩等于秩的和、乘积的秩小于两个矩阵、

联立的秩大于等于最大的小于等于秩的和、乘非零系数秩不变、左乘可逆矩阵秩不变、

右乘可逆矩阵秩不变、左乘列满秩矩阵秩不变、右乘行满秩矩阵秩不变、乘转置矩阵秩不变、

A(mxn)，B(nxs)，AB=O则r(A)+r(B)≤n

求法

1. A为数字矩阵时，作初等变换化为行阶梯矩阵，r（A）= 非零行行数
2. A为抽象矩阵时，用定义或性质

分块矩阵

运算

加法、数乘和普通矩阵一样

乘法：前列后行分发相同

转置：整个矩阵转置了，每个小块里面也要转置

逆：

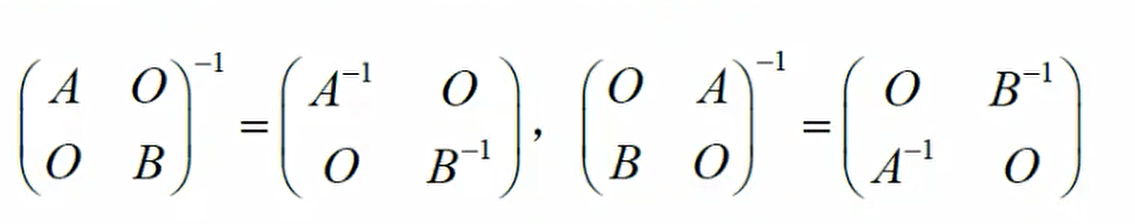
向量

概念

n维向量：n个有次序的数 组成的数组，向量也是矩阵

内积：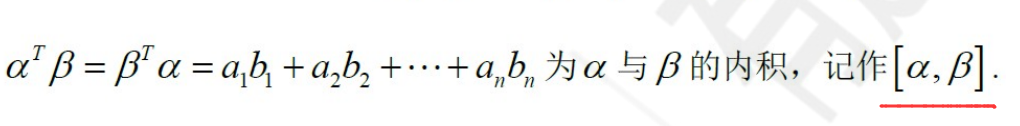

正交：[a, b] = 0，几何上垂直

向量长度：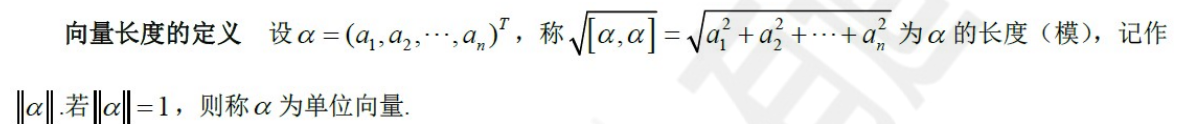

正交矩阵

A为n阶矩阵，A * A^T = A^T * A = E

充要条件

1. A^T = A^(-1)
2. A的列（行）向量组为单位正交的向量组

性质

1. 
2. 

Schmidt正交化

向量组

概念

向量组：若干同维度的列向量组成的集合

线性表示

向量组a1,a2…am，存在一组数λ1,λ2,…,λm，向量组b能由λ1a1 + λ2a2 + … +λmam表示

秩相等才能线性表示

线性表示的充要条件

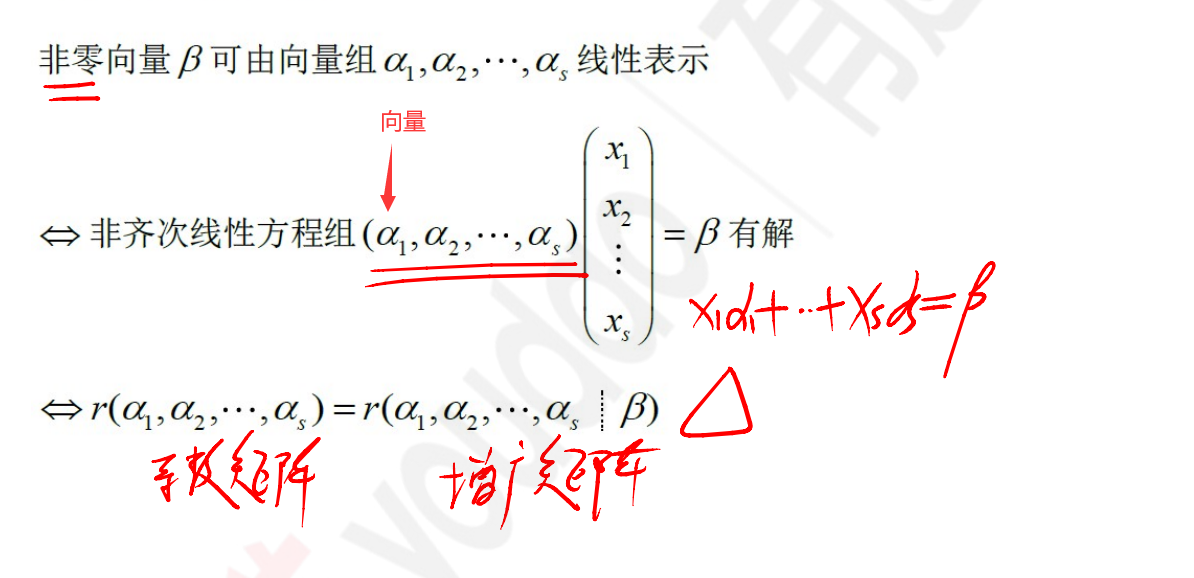
线性表示的求法

求的是系数矩阵

向量组等价

两个向量组可以互相线性表示

向量组等价的充要条件

向量组A与向量组 B

等价的充要条件是R(A) = R(A,B) = R(B)

线性相关

向量组a1,a2,a3…，存在一组非全零的k1,k2,k3…

使得k1a1 + k2a2 + k3a3…. = 0

则为线性相关

两个向量线性相关的几何意义是两个向量共线

三个向量线性相关的几何意义是三个向量共面

一个向量线性相关，则向量为零向量

两个向量线性相关，则两个向量成比例

线性相关的充要条件

线性相关的充分条件

1. 含有零向量的向量组线性相关
2. 部分相关，则整体相关
3. 高维相关，则低维相关
4. 向量组a1,a2,…as可由向量组b1,b2,…bt线性表示，则s>t
5. n+1个n维向量线性相关

向量组的秩

极大线性无关组：A0：a1， a2，…，ar 线性无关，向量组 A 中任意 r+1 个向量都线性相关

称向量组A0是向量组A的一个最大线性无关向量组

秩： r称为向量组 A 的秩

极大线性无关组不唯一

矩阵的秩等于其（行/列）向量组的秩

极大线性无关组的求法：化为行阶梯型矩阵，每行第一个首非零元对应的列向量构成极大线性无关组

线性方程组的解

解向量

若 x1 =ξ11 ，x2 =ξ21，…，xn =ξn 1为方程的解，则x = (ξ11，ξ21，…，ξn1)^T为解向量

基础解系

齐次线性方程组的解集的最大无关组（Ax = 0解的极大线性无关组），

特点：基础解系不唯一、线性无关、能表示其他解

求法：化为行最简型，自由变量取1,0,0…、0,1,0…、….、…0,0,1。最重要的是求出基础解系的秩!!!

解的性质

齐次方程：

1. 若 x =ξ1，x =ξ2 为齐次方程的解，则 x =ξ1 +ξ2 也是齐次方程的解
2. 若 x =ξ1 为齐次方程的解，k 为实数，则 x = kξ1 也是齐次方程的解
3. 设 m×n 矩阵 A 的秩 R（A）= r，则基础解系的秩R = n-r（未知数个数 - 主变量个数）
4. 当矩阵 A 与 B 的列数相等时，要证 R（A）= R（B），只需证明齐次方程 Ax = 0 与 Bx = 0同解

非齐次方程：

1. 设 x =η1 及 x = η2 都是非齐次的解，则 x =η1-η2 为对应的齐次线性方程组的解
2. 设 x =η是非齐次的解，x =ξ是齐次的解，则 x =ξ+η仍是非齐次的解
3. 非齐次方程的通解 =对应的齐次方程的通解+非齐次方程的一个特解
4. 特解求法：增广矩阵化为行最简型，自由变量都取0

是否有解的判断

Ax = 0只有零解 <==> r(A) = n

Ax = 0有非零解 <==> r(A) < n

Ax = b无解 <==> r(A) < r(A的增广) <==> r(A) = r(A的增广) - 1

Ax = b有唯一解 <==> r(A) = r(A的增广) = n

Ax = b有无穷多解 <==> r(A) = r(A的增广) < n

公共解

定义

若a即为线性方程组I的解也为线性方程组II的解，则a为I与II的公共解

求法

1. 知道两个方程组，联立
2. 知道一个方程组和一个方程组的通解，则将通解带入方程组确定参数
3. 知道两个通解，令其相等来确认参数

例题

向量空间

概念

向量空间：

设 V 为 n 维向量的集合，如果集合 V非空，且集合 V 对于向量的加 法及数乘两种运算封闭，那么就称集合 V为向量空间

封闭，是指在集合 V 中可以进行向量的加法及数乘两种运算.具体地说，就是：若 a∈V，b∈V，则 a+b∈V；若 a ∈V， λ∈R，则λa∈V

子空间：

设有向量空间 V1 及 V2，若V1被包含于V2 ，就称 V1 是 V2 的子空间

r维向量空间：

向量组 a1 ，a2 ，…， ar 线性无关，V中向量可由这个向量组表示

就称为向量空间 V 的一个基（极大无关组），r称为向量空间V的维数（秩），并称V为r维向量空间

0维向量只含一个零向量

单位坐标向量组e1,e2,e3…组成的基称为自然基

坐标：

在向量空间 V 中取定一个基 a1，a2，… ，ar，那么 V 中任一向量 x 可惟一地表示为

x =λ1 a1 +λ2 a2 + … +λr ar

数组λ1，λ2， …，λr 称为向量量x在基a1，a2 ，… ，ar 中的坐标

性质

1. n元齐次方程的解集是一个向量空间
2. n元非齐次方程的解集不是一个向量空间

过渡矩阵

相似矩阵

内积

定义

x = (x1,x2,x3…,xn)^T

y = (y1,y2,y3…,yn)^T

内积：[x,y] = x1y1 + x2y2 + x3y3 … + xnyn，结果是一个实数

长度：||x|| = √[x,x] = √(x1^2 + x2^2 + …)

夹角：arccos ( [x, y] / ||x|| ||y|| )

当[x, y] = 0时，向量间正交（垂直）

x=0与任何向量正交

性质

• [x，y] = [y，x]
• [λx，y] = λ[x，y]
• [x+y，z] = [x，z] + [y，z]
• 当 x = 0 时，[x，x] = 0；当 x≠0时，[x，x]＞0
• 施瓦茨（Schwarz）不等式：[x,y]^2 <= [x,x] [y, y]

正交向量组

定义

正交向量组：一组两两正交的非零向量

标准正交基：一个基e1，…，er 两两正交，且都是单位向量

单位向量：||x|| = 1

单位化：x = a / ||a||

性质

• 若 n 维向量 a1，a2， … ，ar 是一组两两正交的非零向量，则 a1， a2，…，ar线性无关

施密特正交化

正交矩阵

定义

正交矩阵：A^T A = E （即 A ^(-1) = A^T）

正交变换：若P为正交矩阵，则线性变换y=Px称为正交变换

性质

• A 的列向量都是单位向量，且两两正交
• 若 A 为正交矩阵，则 A^(-1) = A^T 也是正交矩阵，且|A| = 1 或（-1）
• 若 A 和 B 都是正交矩阵，则 A B 也是正交矩阵
• 正交变换后线段长度不变：||y|| = √(y^T y) = √(x^T p^T p x) = √(x^T x) = ||x||
• |A+E| = 0

相似矩阵

定义

有可逆矩阵P，使得P^-1 A P = B，称A与B相似，记作A~B

性质

• A和B相似，则特征多项式、特征值、行列式、秩、迹（对角线元素之和）相同
• 若n阶矩阵A与对角矩阵相似，则对角线上元素λ1，λ2，…，λn 即是 A 的n个特征值
• n 阶矩阵 A 与对角矩阵相似（即 A 能对角化）的充分必要条件是 A 有 n 个线性无关的特征向量
• 如果 n 阶矩阵 A 的 n 个特征值互不相等，则 A 与对角矩阵相似

充要条件

n阶矩阵可相似对角化 <==>

A有n个线性无关的特征向量 <==>

k重特征值有k个线性无关的特征向量

充分条件

n阶矩阵可相似对角化 <==

1. A有n个不同的特征值
2. A为实对称矩阵（A = A^T）

相似矩阵例题

特征值、特征向量

定义

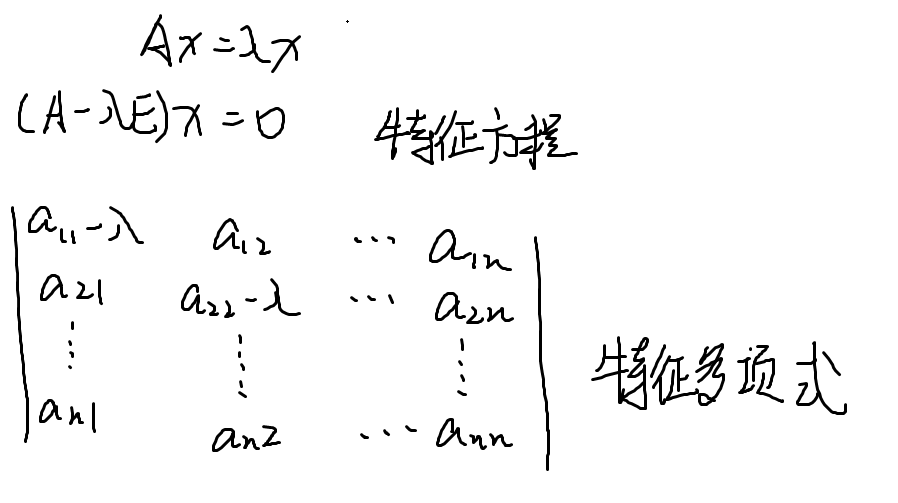
特征值：设A是n阶矩阵，如果数λ和 n 维非零列向量 x 使关系式 A x =λx成立，那么数λ称为矩阵A的特征值

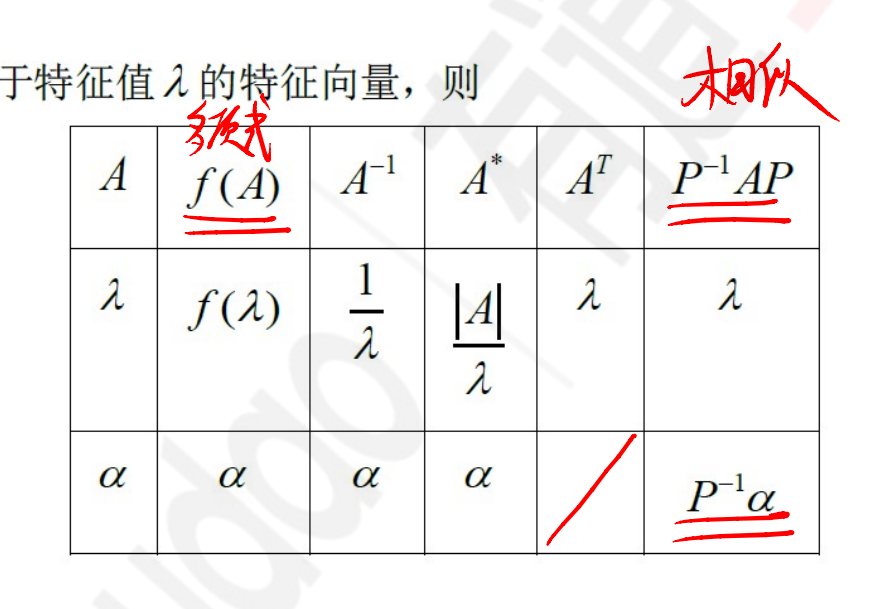
特征向量：非零向量x称为A的对应于特征值λ的特征向量

特征方程和特征多项式：

性质

1. λ1 +λ2 +…+λn = a11 +a22 +…+ann = tr(A)（特征值之和等于对角线元素相加）
2. λ1 λ2 … λn = |A|。若特征值不全为0，则A可逆
3. 若r(A) = 1，则λ1 = α^Tβ = αβ^T = tr(A)，其他特征值为0（α为极大无关组，β为系数）
4. n阶矩阵有n个特征值
5. 若λ是 A 的特征值，则λ^k 是 A^k 的特征值
6. 若λ是 A 的特征值，则φ（λ）是 φ（A）的特征值（其中φ（λ）= a0 +a1λ+…+am λ^m 是λ的多项式，φ（A）= a0 E + a1 A +…+am A^m 是矩阵 A 的多项式）
7. 特征值各不相同，对应的特征向量线性无关
8. 两个特征值不同，对应的向量组线性无关
9. 不同特征值的特征向量之和不是特征向量
10. 

例题

实对称矩阵

性质

• 特征值均为实数
• 实对称矩阵可相似对角化
• r(A) = 非零特征值的个数
• 不同特征值的特征向量正交
• k重特征值有k个线性无关的特征向量
• 设 A 为 n 阶对称矩阵，则必有正交矩阵 P，使 P^-1 A P = P^T A P =Λ，其 中Λ 是以 A 的 n 个特征值为对角元的对角矩阵

实对称矩阵对角化

步骤

1. 求n个特征值λ1，…，λn
2. 求n个线性无关的特征向量
3. 将特征向量正交化、单位化得正交矩阵P，从而P^-1 A P = P^T A P = Λ

知特征值和特征向量求原矩阵

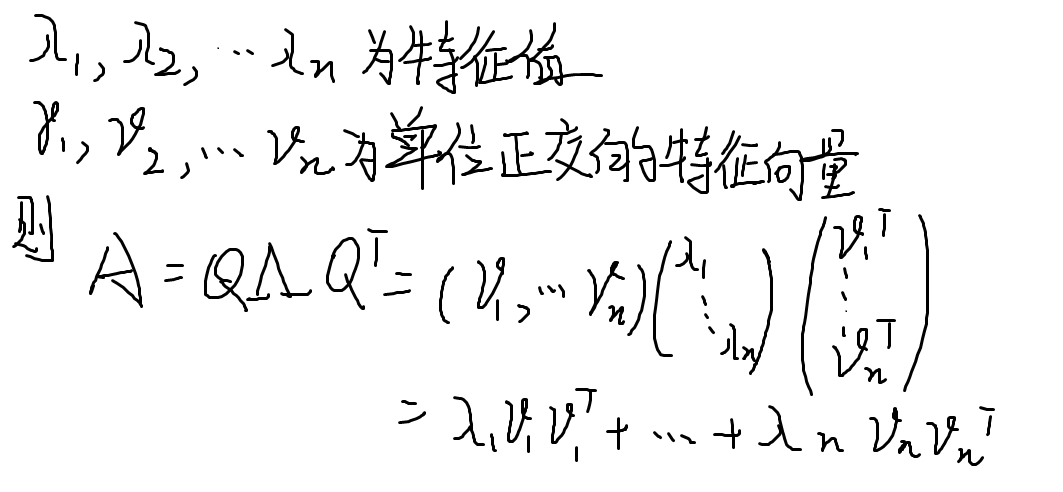
例题

二次型

二次型

定义

含有 n 个变量 x1， x 2 ，… ， xn 的二次齐次函数 f(x1, x2, …, xn) = (a11 x1^2) + (a22 x2^2) + … + (ann xn^2) + (2a12 x1 x2) + (2a13 x1 x3) + … + (2an-1,n xn-1 xn)，称为二次型

二次型可以用矩阵记作f = x^T A x，A为实对称矩阵，实对称矩阵和二次型一一对应

秩：实对称矩阵A的秩就为二次型的秩

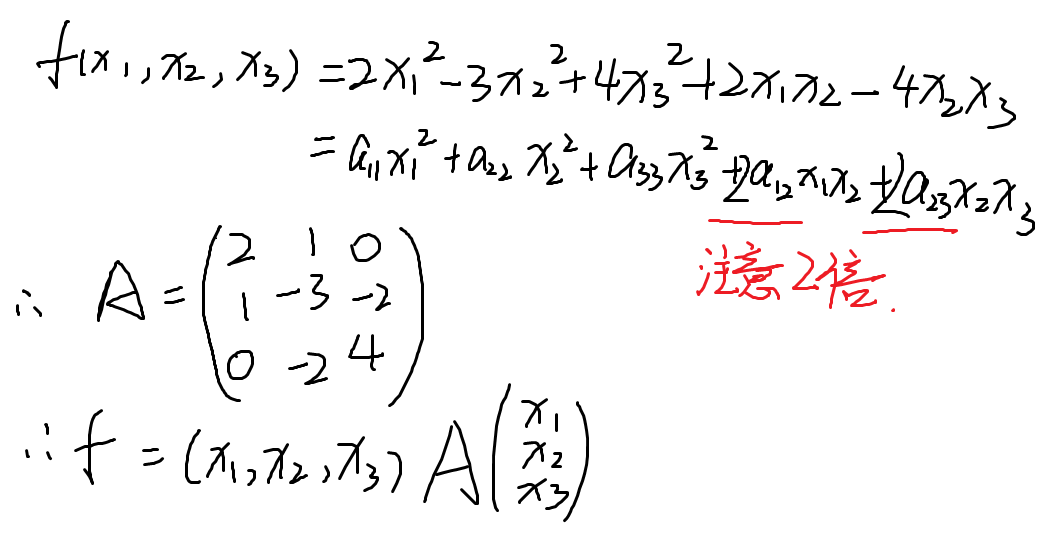
二次型(例题)

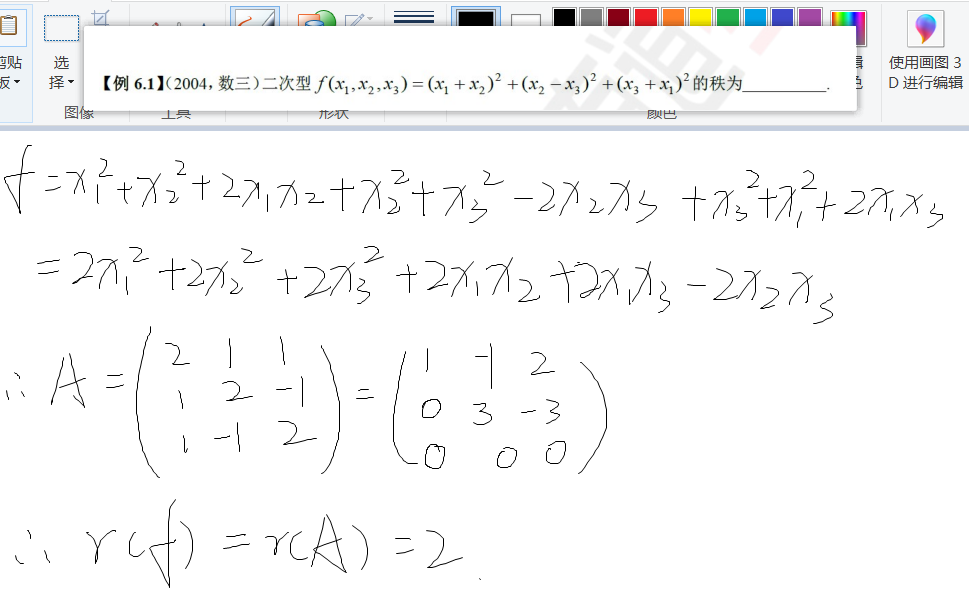
标准型、规范型

标准型：只含平方项的二次型

规范型：系数都为1、-1、0的标准型

正惯性指数p：标准型中系数为正的个数

负惯性指数q：标准型中系数为负的个数

惯性定理：二次型的标准型不是唯一的，但标准型的正负惯性指数个数是相同的

合同矩阵

定义

充要条件

A、B合同 <==>

r(A) = r(B) <==>

二次型x^T A x 和x^T B x有相同的正、负惯性指数 <==>

A、B有相同的正、负特征值的个数

二次型化标准型求法

• 正交变换法

1. 求A的n个特征值
2. 求A的n个线性无关的特征向量
3. 将特征向量正交化得正交矩阵Q，x = Qy，二次型化为标准型f = (λ1 y1^2) + (λ2 y2^2) + … + (λn yn^2)

• 拉格朗日配方法

标准型(例题)

正定二次型

定义

二次型f = x^T A x，对任意的x ≠ 0，有x^T A x > 0，则f为正定二次型，A为正定矩阵

如果x^T A x < 0，则为负定二次型

充要条件

f = x^T A x正定 <==>

• 正惯性指数为n
• A与E合同，则存在可逆矩阵C，使得C^T A C = E
• A的特征值均大于0
• A的顺序主子式均大于0

正定二次型(例题)