深度学习

深度学习

常见深度学习模型

  • 卷积神经网络(Convolutional Neural Networks，CNN)
    • 主要用于图像处理，如图像分类、目标检测、图像分割等
    • 特点是使用卷积层来自动提取图像的局部特征，并通过池化层减少参数数量，提高计算效率
  • 循环神经网络(Recurrent Neural Networks，RNN)
    • 适用于处理序列数据，例如自然语言处理（NLP）、语音识别等
  • 自编码器(Autoencoders)
    • 一种无监督学习模型，通常用于降维、特征学习或者异常检测
  • 生成对抗网络(Generative Adversarial Networks，GAN)
    • 包含生成器和判别器，生成器负责创建看起来真实的假样本，判别器负责区分真假
    • 广泛用于图像合成、视频生成领域
  • Transformer
    • 主要用于自然语言处理任务
  • 深度强化学习(Deep Reinforcement Learning，DRL)
  • 图神经网络(GNN,Graph Neural Network)

Pytorch

PyTorch 是一个开源的深度学习框架，主要用于构建、训练和部署神经网络模型。

官方文档

安装

  • 创建新的anaconda环境：conda create -n 环境名 python=版本
  • 切换环境：conda activate 环境名
  • 安装Pytorch：pip install torch
  • 安装NumPy：pip install numpy（不安装使用torch时会有警告）

Tensor张量

pytorch中的数据结构，类似于NumPy的ndarray，并支持GPU加速

可看做是多维数组 + 能自动求导

创建Tensor的方式

  1. 直接创建

    data: 数据, dtype: 可指定元素类型,默认float32

    torch.tensor(data, dtpye)：创建Tensor的函数（推荐用这个）

    1
    2
    3
    4
    # 创建一维的标量
    t1 = torch.tensor(10)
    print(f't1: {t1}, type: {type(t1)}')
    # t1: 10, type: <class 'torch.Tensor'>

  2. 使用python数组创建

    1
    2
    3
    4
    5
    arr = [[1, 2], [3, 4]]
    t2 = torch.tensor(arr)
    print(f't2: {t2}, type: {type(t2)}')
    # t2: tensor([[1, 2],
    #         [3, 4]]), type: <class 'torch.Tensor'>

  3. 使用numpy的ndarray创建

    1
    2
    3
    4
    5
    6
    data = np.array([[1, 2], [3, 4], [5, 6]])
    t3 = torch.tensor(data)
    print(f't3: {t3}, type: {type(t3)}')
    # t3: tensor([[1, 2],
    #         [3, 4],
    #         [5, 6]]), type: <class 'torch.Tensor'>

  4. torch.Tensor()方式

    torch.Tensor()：Tensor的构造函数

    1
    2
    3
    4
    5
    # 创建2行3列的Tensor
    t4 = torch.Tensor(2, 3)
    print(f't4: {t4}, type: {type(t4)}')
    # t4: tensor([[2.3420e+18, 1.8581e-42, 0.0000e+00],
    #         [0.0000e+00, 0.0000e+00, 0.0000e+00]]), type: <class 'torch.Tensor'>

  5. 创建线性张量

    1
    2
    3
    4
    5
    6
    7
    8
    9
    # 指定范围，左闭右开
    t1 = torch.arange(0, 10, 2)
    print(f't1: {t1}, type: {type(t1)}')
    # t1: tensor([0, 2, 4, 6, 8]), type: <class 'torch.Tensor'>

    # 等差数列
    t2 = torch.linspace(0, 10, 4)
    print(f't2: {t2}, type: {type(t2)}')
    # t2: tensor([ 0.0000,  3.3333,  6.6667, 10.0000]), type: <class 'torch.Tensor'>

  6. 创建随机值的张量

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    # 设置随机种子，默认采用当前时间戳
    # torch.initial_seed()

    # 设置随机种子，可手动指定值
    torch.manual_seed(3)

    # 创建随机张量，符合均匀分布
    t1 = torch.rand(size=(2, 3))
    print(f't1: {t1}, type: {type(t1)}')
    # t1: tensor([[0.6203, 0.8253, 0.1595],
    #         [0.6263, 0.2207, 0.9387]]), type: <class 'torch.Tensor'>

    # 创建随机张量，符合正态分布
    t2 = torch.randn(size=(2, 3))
    print(f't2: {t2}, type: {type(t2)}')
    # t2: tensor([[ 0.7625,  1.4948, -0.5175],
    #         [-0.4186, -0.9309,  0.4139]]), type: <class 'torch.Tensor'>

    # 创建随机张量，都是整数
    t3 = torch.randint(low=0, high=2, size=(2, 3))
    print(f't3: {t3}, type: {type(t3)}')

  7. 创建有指定值的张量

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    # 创建全是1的张量
    t1 = torch.ones(2, 3)
    print(f't1: {t1}, type: {type(t1)}')
    # t1: tensor([[1., 1., 1.],
    #         [1., 1., 1.]]), type: <class 'torch.Tensor'>

    # 根据已有张量，创建size一样的全1张量
    t2 = torch.tensor([[1, 2], [3, 4], [5, 6]])
    t3 = torch.ones_like(t2)
    print(f't3: {t3}, type: {type(t3)}')
    # t3: tensor([[1, 1],
    #         [1, 1],
    #         [1, 1]]), type: <class 'torch.Tensor'>

    # 创建全是0的张量
    t4 = torch.zeros(2, 3)
    print(f't4: {t4}, type: {type(t4)}')
    # t4: tensor([[0., 0., 0.],
    #         [0., 0., 0.]]), type: <class 'torch.Tensor'>

    # 创建全是指定值的张量
    t5 = torch.full(size=(2, 3), fill_value=255)
    print(f't5: {t5}, type: {type(t5)}')
    # t5: tensor([[255, 255, 255],
    #         [255, 255, 255]]), type: <class 'torch.Tensor'>

元素类型转换

1
2
3
4
5
6
7
8
t1 = torch.tensor([1, 2, 3, 4])
print(f't1: {t1}, data_type: {t1.dtype}')
# t1: tensor([1, 2, 3, 4]), data_type: torch.int64

# 转换为float类型
t2 = t1.type(torch.float)
print(f't2: {t2}, data_type: {t2.dtype}')
# t2: tensor([1., 2., 3., 4.]), data_type: torch.float32

常见类型

dtype 位数
torch.float64 / torch.double 64bit
torch.float32（默认） 32bit
torch.float16 / torch.half 16bit
torch.int64 / torch.long（默认） 64bit
torch.int32 32bit
torch.int16 / torch.short 16bit

张量和ndarray互转

  1. 张量 -> ndarray，浅拷贝

    1
    2
    3
    4
    5
    6
    7
    8
    # 浅拷贝
    t1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
    n1 = t1.numpy()

    t1[0][0] = 2
    print(f'n1: {n1}, type: {type(n1)}')
    # n1: [[2 2 3]
    #  [4 5 6]], type: <class 'numpy.ndarray'>

  2. 张量 -> ndarray，深拷贝

    1
    2
    3
    4
    5
    6
    7
    8
    # 深拷贝
    t1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
    n1 = t1.numpy().copy()

    t1[0][0] = 2
    print(f'n1: {n1}, type: {type(n1)}')
    # n1: [[1 2 3]
    #  [4 5 6]], type: <class 'numpy.ndarray'>

  3. ndarray -> 张量，浅拷贝

    1
    2
    3
    4
    5
    6
    n1 = np.array([1, 2, 3])
    t1 = torch.from_numpy(n1)

    n1[0] = 100
    print(f't1: {t1}, type: {type(t1)}')
    # t1: tensor([100,   2,   3]), type: <class 'torch.Tensor'>

  4. ndarray -> 张量，深拷贝

    1
    2
    3
    4
    5
    6
    n1 = np.array([1, 2, 3])
    t1 = torch.tensor(n1)

    n1[0] = 100
    print(f't1: {t1}, type: {type(t1)}')
    # t1: tensor([1, 2, 3]), type: <class 'torch.Tensor'>

张量运算

  1. 和数进行加减乘除

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    t1 = torch.tensor([1, 2, 3])

    # 加法，不修改元数据
    print(t1.add(10))
    print(t1 + 10)
    # 加法，修改元数据
    t1.add_(10)
    print(t1)

    t1 = torch.tensor([1, 2, 3])
    # 减法，不修改元数据
    print(t1.sub(10))
    print(t1 - 10)
    # 减法，修改元数据
    t1.sub_(10)
    print(t1)

    t1 = torch.tensor([1, 2, 3])
    # 乘法，不修改元数据
    print(t1.mul(10))
    print(t1 * 10)
    # 乘法，修改元数据
    t1.mul_(10)
    print(t1)

    t1 = torch.tensor([1, 2, 3], dtype=torch.float)
    # 除法，不修改元数据
    print(t1.div(10))
    print(t1 / 10)
    # 除法，修改元数据
    t1.div_(10)
    print(t1)

  2. 矩阵点乘

    对应元素相乘

    1
    2
    3
    4
    5
    6
    t1 = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
    t2 = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
    print(t1 * t2)
    # tensor([[ 1,  4,  9],
    #         [16, 25, 36],
    #         [49, 64, 81]])

  3. 矩阵乘法

    行乘列

    1
    2
    3
    4
    5
    6
    t1 = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
    t2 = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
    print(t1 @ t2)
    # tensor([[ 30,  36,  42],
    #         [ 66,  81,  96],
    #         [102, 126, 150]])

张量数学与统计函数

方法 作用
x.sum(dim) 求和
x.mean(dim) 均值，需要dtype=torch.float
x.max(dim) 最大值
x.min(dim) 最小值
x.argmax(dim) 最大值索引
x.argmin(dim) 最小值索引
x.std(dim) 标准差
x.var(dim) 方差
x.pow(p) 幂运算
torch.sqrt(x) 开方
torch.exp(x) 指数
torch.abs(x) 绝对值
torch.log(x) 对数
…

张量索引

1
2
3
4
5
6
7
8
9
torch.manual_seed(23)

t1 = torch.randint(1, 10, (5, 5))
print(t1)
# tensor([[7, 9, 4, 2, 6],
#         [3, 5, 1, 1, 3],
#         [1, 2, 1, 4, 8],
#         [2, 3, 1, 8, 5],
#         [7, 4, 3, 4, 5]])

  1. 简单行列索引

    1
    2
    3
    4
    5
    6
    print(t1[1])
    # tensor([3, 5, 1, 1, 3])
    print(t1[:, 2])
    # tensor([4, 1, 1, 1, 3])
    print(t1[0, :])
    # tensor([7, 9, 4, 2, 6])

  2. 列表索引

    第一个列表表示行，第二个列表表示列

    如果列表里只有1个元素，那么就会和另一个列表逐一匹配

    如果两个列表元素数量都大于1,且数量不同，就会报错

    1
    2
    3
    4
    5
    6
    print(t1[[1], [2, 3, 4]])
    # tensor([1, 1, 3])
    print(t1[[0, 1], [0, 0]])
    # tensor([7, 3])
    print(t1[[0, 1], [0, 2, 3]])
    # 报错

  3. 范围索引（切片）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    print(t1[:3, :2])
    # tensor([[7, 9],
    #         [3, 5],
    #         [1, 2]])

    # 所有行为奇数，列为偶数的元素
    print(t1[::2, 1::2])
    # tensor([[9, 2],
    #         [2, 4],
    #         [4, 4]])

    # 条件索引
    print(t1[t1[:, 2] > 3])
    # tensor([[7, 9, 4, 2, 6]])

张量形状

都属于浅拷贝，如果要深拷贝，就在方法名后面加上_

  1. reshape()：修改形状

    1
    2
    3
    4
    5
    6
    7
    8
    t1 = torch.randint(1, 10, (2, 3))

    print(f'shape of t1:{t1.shape}')
    # shape of t1:torch.Size([2, 3])

    t2 = t1.reshape((1, 6))
    print(f'shape of t2:{t2.shape}')
    # shape of t2:torch.Size([1, 6])

  2. unsqueeze(): 在指定位置插入大小为1的维数

    1
    2
    3
    4
    5
    6
    7
    8
    t1 = torch.randint(1, 10, (2, 3))

    print(f'shape of t1:{t1.shape}')
    # shape of t1:torch.Size([2, 3])

    t2 = t1.unsqueeze(0)
    print(f'shape of t2:{t2.shape}')
    # shape of t2:torch.Size([1, 2, 3])

  3. squeeze()：删除所有大小为1的维度

    1
    2
    3
    4
    t1 = torch.randint(1, 10, (3, 1, 1, 2, 1))
    t2 = t1.squeeze()
    print(f'shape of t2:{t2.shape}')
    # shape of t2:torch.Size([3, 2])

  4. transpose()：交换两个维度，二维相当于转置了

    1
    2
    3
    4
    t1 = torch.randint(1, 10, (2, 3, 5))
    t2 = t1.transpose(0, 2)
    print(f'shape of t2:{t2.shape}')
    # shape of t1:torch.Size([5, 3, 2])

  5. permute()：返回按照指定顺序排序的张量

    1
    2
    3
    4
    t1 = torch.randint(1, 10, (2, 3, 5))
    t2 = t1.permute(0, 2, 1)
    print(f'shape of t2:{t2.shape}')
    # shape of t2:torch.Size([2, 5, 3])

  6. view()：修改内存和张量中数的位置一样的张量形状，位置不一致时调用报错

    transpose()：返回一个内存和张量中数的位置一样的张量

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    t1 = torch.tensor([[1, 2, 3], [4, 5, 6]])

    t2 = t1.transpose(0, 1)
    print(f'{t2.is_contiguous()}')  # False，转置后和内存中位置不一样了
    print(f'{t2}')
    # tensor([[1, 4],
    #         [2, 5],
    #         [3, 6]])

    t3 = t2.contiguous()
    print(f'{t3.is_contiguous()}')  # True
    print(f'{t3.view(2, 3)}')
    # tensor([[1, 4, 2],
    #         [5, 3, 6]])

张量拼接

  1. cat()：拼接指定维度的张量

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    t1 = torch.randint(1, 10, (2, 3))
    t2 = torch.randint(1, 10, (2, 3))
    print(f't1:{t1}\nt2:{t2}')
    # t1:tensor([[1, 1, 3],
    #         [7, 3, 8]])
    # t2:tensor([[4, 5, 2],
    #         [4, 6, 1]])

    # 除了拼接的维度数，其他维度数要一致
    t3 = torch.cat([t1, t2], dim=0)
    print(t3)
    # tensor([[1, 1, 3],
    #         [7, 3, 8],
    #         [4, 5, 2],
    #         [4, 6, 1]])

  2. stack()：沿新维度连接张量，需要所有维度都相等

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    t1 = torch.randint(1, 10, (2, 3))
    t2 = torch.randint(1, 10, (2, 3))
    print(f't1:{t1}\nt2:{t2}')
    # t1:tensor([[3, 1, 9],
    #         [6, 6, 7]])
    # t2:tensor([[8, 7, 6],
    #         [6, 5, 7]])

    # 所有维度数要一致
    t3 = torch.stack([t1, t2])
    print(t3)
    # tensor([[[3, 1, 9],
    #          [6, 6, 7]],
    # 
    #         [[8, 7, 6],
    #          [6, 5, 7]]])
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    t1 = torch.randint(1, 10, (2, 3))
    t2 = torch.randint(1, 10, (2, 3))
    print(f't1:{t1}\nt2:{t2}')
    # t1:tensor([[4, 2, 2],
    #         [9, 7, 8]])
    # t2:tensor([[9, 4, 4],
    #         [9, 6, 1]])

    # 所有维度数要一致
    t3 = torch.stack([t1, t2], dim=1)
    print(t3)
    # tensor([[[4, 2, 2],
    #          [9, 4, 4]],
    # 
    #         [[9, 7, 8],
    #          [9, 6, 1]]])

自动微分

前向传播：数据从输入层进入，经过每一层的权重计算和激活函数，最后得到一个预测值。我们将预测值与真实值对比，计算出损失（Loss/Error）。

反向传播：从损失函数出发，逆向计算损失对每一层参数（权重 w 和偏置 b）的梯度。

基本使用

sum()：计算张量中所有元素的总和

backward()：反向传播计算梯度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 权重
# requires_grad：是否自动求导
w = torch.tensor([10, 20], dtype=torch.float, requires_grad=True)

for i in range(100):
    # 损失函数,也是一个张量
    loss = 2 * w ** 2 + 10
    print(f'loss: {loss}')

    # sum()把两个权重的损失函数加起来，变成一个标量，然后分别求偏导
    loss.sum().backward()

    # 更新权重，前面反向传播后算出来的梯度在w.grad中
    w.data -= 0.01 * w.grad
    print(f'w: {w}')

    # 梯度会自动累加，需要手动清零
    w.grad.zero_()

注意：

​ 要从设置了requires_grad = True的tensor中获取ndarray，需要使用x.detach().numpy()来获取

1
2
3
4
5
6
7
8
9
10
x = torch.tensor([1.0], requires_grad=True)
y = x * 2

# detach()得到的tensor，不会参与自动求导
z = y.detach().numpy()

z[0] = 1000

y.backward()
print(x.grad)   # tensor([2.])

代码

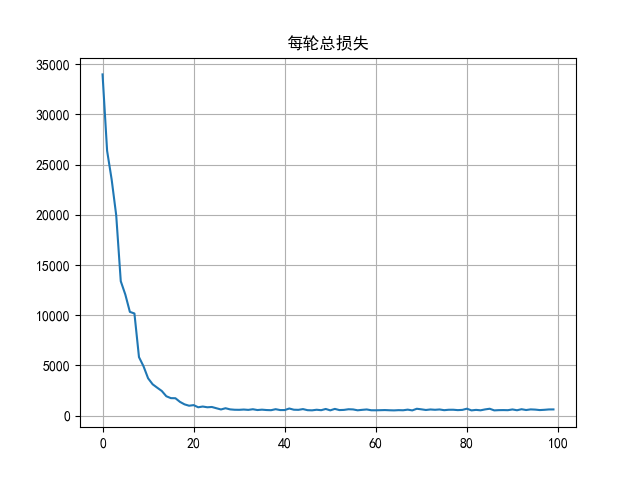
线性回归案例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
import torch
from torch.utils.data import TensorDataset  # 把特征和标签绑定在一起
from torch.utils.data import DataLoader     # 数据加载与批处理器
from torch import nn
from torch import optim                     # 优化器，自动调整参数
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression    # 生成数据集

def create_dataset():
    x, y, coef = make_regression(
        n_samples=100,      # 样本数量
        n_features=1,       # 特征数量
        noise=10,           # 噪声
        coef=True,
        random_state=1      # 随机种子
    )

    return (torch.tensor(x, dtype=torch.float),
            torch.tensor(y, dtype=torch.float),
            coef)

def train_model(x, y, coef):
    # 数据集
    dataset = TensorDataset(x, y)

    # 批处理器
    dataloader = DataLoader(dataset, batch_size=16, shuffle=True)

    # 线性回归模型
    # in_features: 输入特征维度, out_features: 输出特征维度
    model = nn.Linear(in_features=1, out_features=1)

    # 损失函数
    criterion = nn.MSELoss()

    # 优化器
    # 模型参数，学习率
    optimizer = optim.SGD(model.parameters(), lr=0.01)

    # 训练整个数据集的轮次
    epochs = 100
    # 记录每轮的总损失
    losses = []

    for _ in range(epochs):
        total_loss = 0
        for train_x, train_y in dataloader:
            # 预测
            y_pred = model(train_x)

            # 计算损失
            loss = criterion(y_pred, train_y.reshape(-1, 1))
            total_loss += loss.item()

            # 反向传播
            loss.sum().backward()

            # 更新参数
            optimizer.step()
            optimizer.zero_grad()
        losses.append(total_loss)

    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.title('每轮总损失')
    plt.plot(range(epochs), losses)
    plt.grid()
    plt.show()


if __name__ == '__main__':
    x, y, coef = create_dataset()
    train_model(x, y, coef)

激活函数

作用是为神经网络引入非线性因素，如果没有激活函数，输出都是输入的线性组合，与没有隐藏层效果相当

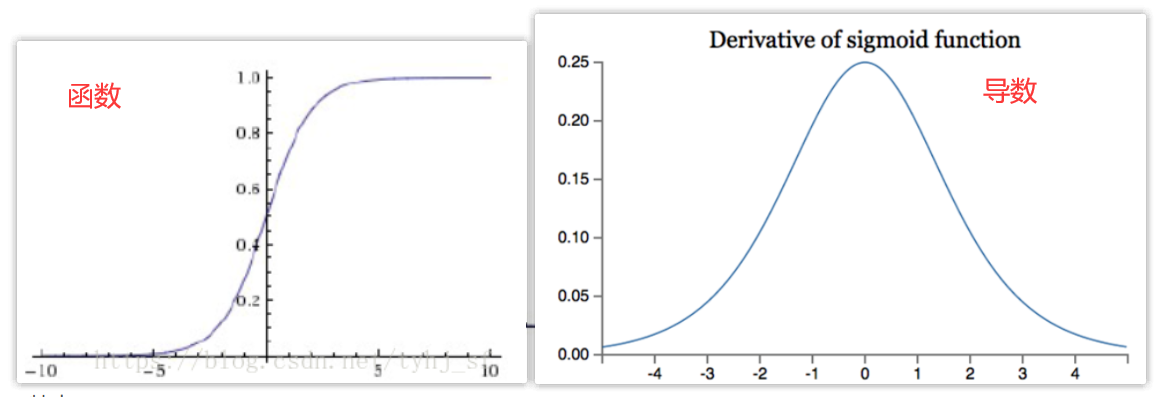
Sigmoid

作用：把输入值映射到[0, 1]区间上，多用于二分类

缺点：

  1. Sigmoid的导数最大值为0.25，反向传播时会让值变小，在多层的神经网络中会导致梯度消失
  2. 只能用于浅层网络
  3. 幂运算相对耗时

公式

图像

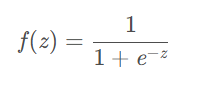
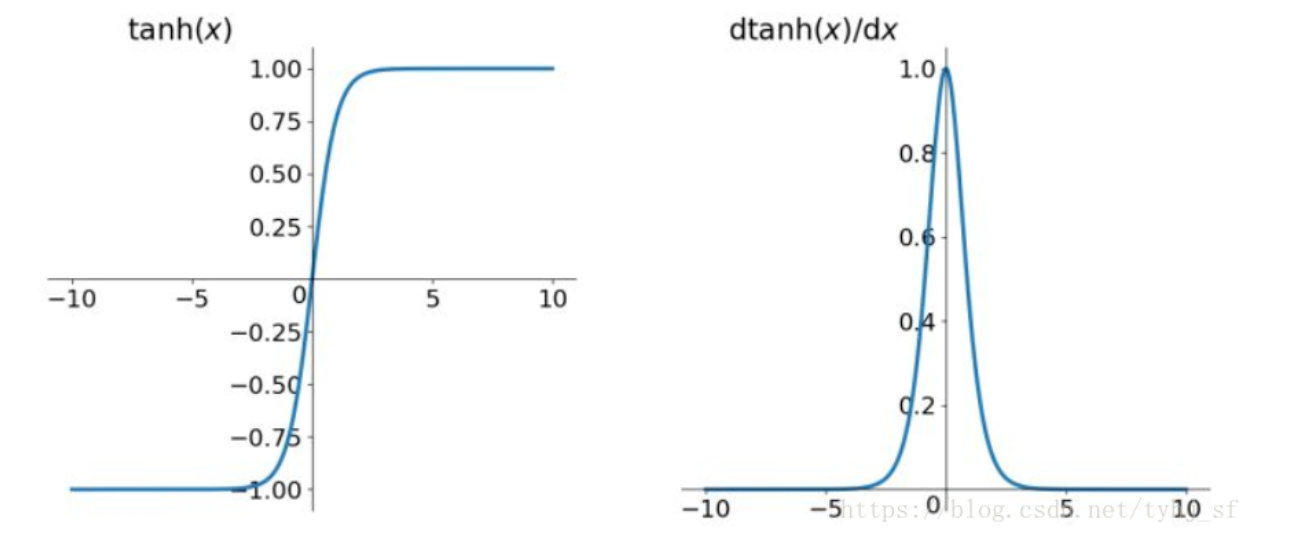
Tanh

作用：把输入值映射到[-1, 1]区间上

优点：

  1. 梯度大，比Sigmoid收敛速度快

公式

图像

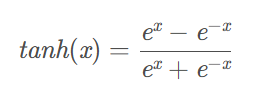
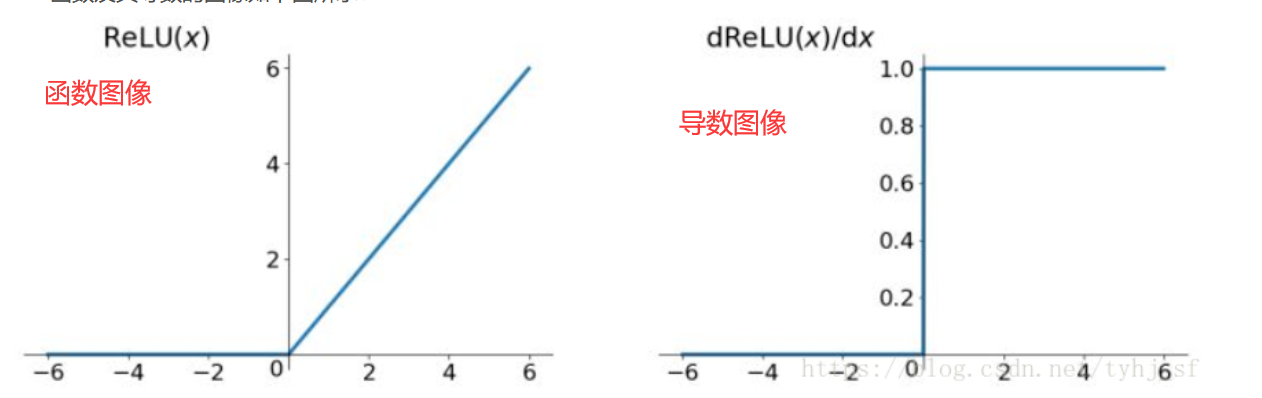
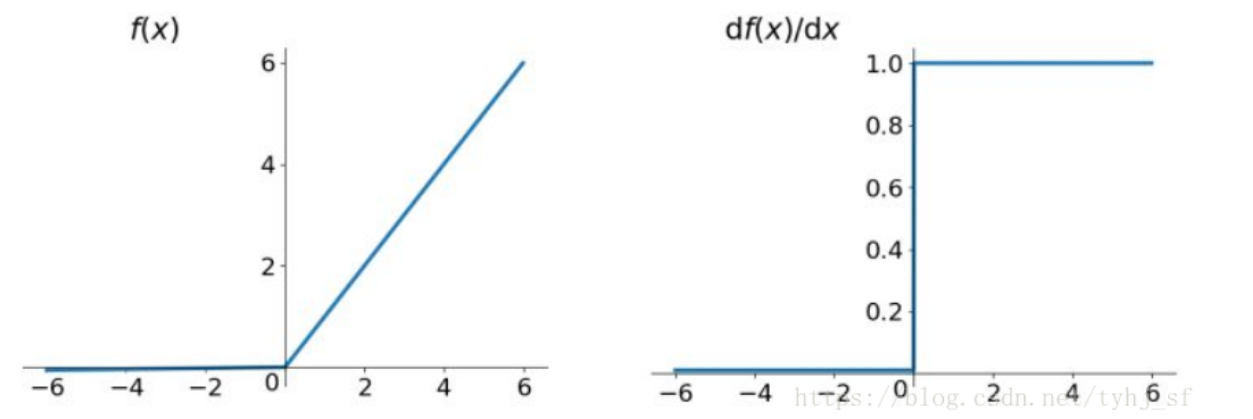
ReLU

作用：只取正数

优点：

  1. 简单效果好，计算速度快
  2. 收敛速度快于Sigmoid和Tanh

缺点：

  1. Dead ReLU Problem：指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新

公式

图像

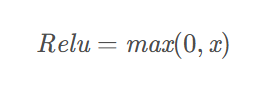
Leaky ReLU

作用：将ReLU的前半段设为αx而非0，通常α = 0.01，解决ReLU的Dead ReLU Problem

公式

图像

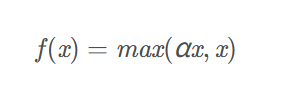
Softmax

作用：用于多分类，是Sigmoid的推广；选择概率最大的为输出

公式

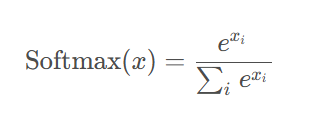
神经网络搭建

参数初始化

给每个神经元的权重和偏置赋予一个初始值的过程

常用的初始化方式：

  1. 全0/1初始化
    • 将所有的权重设为0/1
    • 问题：会导致对称性问题。反向传播时每一层的梯度都相同，网络退化为一个单神经元模型。
  2. 随机初始化
    • 从正态分布或均匀分布中随机采样
    • 使用场景：浅层网络或简单的实验
  3. Xavier 初始化
    • 为了保持信号在穿过每一层网络时方差不变，，从而避免梯度消失或爆炸，适用于 Sigmoid / Tanh
  4. He 初始化
    • 为了保持信号在穿过每一层网络时方差不变，，从而避免梯度消失或爆炸，适用于 ReLU

损失函数

多分类交叉熵损失函数

Cross-Entropy Loss，用于多分类任务

  • 预测值是将最后的输出值通过Softmax激活函数得来
  • 因此最后输出层不用激活函数
  • 经过log()后，如果模型给正确类别预测的概率接近1，那么损失函数接近0
  • 如果模型给正确类别预测的概率越小，那么损失函数接近无穷大

二分类任务损失函数

Binary Cross-Entropy Loss，简称 BCE

  • 模型预测为类别为1的概率
  • 标签为1时看左边，预测值越大，损失越小
  • 标签为0时看右边，预测值越小，损失越小

回归任务损失函数

  • Mean Absolute Error（MAE），平均绝对误差，也称为L1 Loss

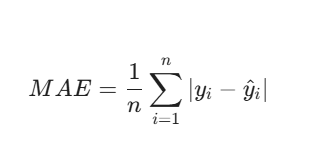
    • 优点：对离群点更具鲁棒性，不会像 MSE 那样被极值带偏。
    • 缺点：在误差接近0的地方导数不连续（不可导），这可能导致模型在收敛最后阶段出现震荡。

  • Mean Squared Error（MSE），均方误差，也称为L2 Loss，最常用

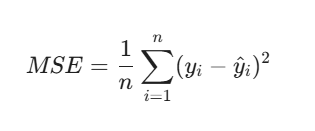
    • 通过平方放大误差。如果预测值离真实值很远，损失会迅速增加。
    • 优点：数学性质极佳（处处可导），有利于使用梯度下降法求解。
    • 缺点：对离群点非常敏感。如果数据中有一个极端的噪声点，MSE 会为了弥补这个大误差而带偏整个模型。

  • Huber Loss，平滑平均绝对误差

    • 是 MSE 和 MAE 的折中方案，结合了两者的优点
    • 当误差较小时，它像 MSE，解决L1零点不可导的问题
    • 当误差较大时，它像 MAE，解决L2离群点导致的梯度爆炸问题

代码

参数初始化示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
linear = nn.Linear(5,3)

# 初始化权重：从均匀分布中抽取值
nn.init.uniform_(linear.weight)
# 初始化参数
nn.init.uniform_(linear.bias)
print(linear.weight)
print(linear.bias)

# 同理
# 初始化成常数  nn.init.constant_(w, 0.3)
# 初始化成全零  nn.init.zeros_(w)
# 从正态分布里抽取值：nn.init.normal_(w)
# kaiming正态分布/均匀分布：nn.init.kaiming_uniform(w)
# xavier正态分布/均匀分布：nn.init.xavier_uniform(w)

神经网络搭建示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import torch
import torch.nn as nn
from torchsummary import summary    # 查看模型结构


# 继承nn.Module
class MyNet(nn.Module):
    # 构建网络结构
    def __init__(self):
        super().__init__()
        self.linear1 = nn.Linear(3, 3)
        self.linear2 = nn.Linear(3, 2)
        self.linear3 = nn.Linear(2, 2)

        # 初始化
        nn.init.xavier_normal(self.linear1.weight)
        nn.init.zeros_(self.linear1.bias)

        nn.init.kaiming_normal(self.linear2.weight)
        nn.init.zeros_(self.linear2.bias)

    # 前向传播
    def forward(self, x):
        x = torch.sigmoid(self.linear1(x))
        x = torch.relu(self.linear2(x))
        x = torch.softmax(self.linear3(x), dim=-1)

        return x

def train():
    model = MyNet()

    # 10个样本，3个特征
    data = torch.randn(10, 3)
    print(f'{data.shape}')  # (10, 3)

    # 一次前向传播
    output = model(data)
    print(f'{output.shape}')    # (10, 2)

    # 输出模型相关参数
    summary(model, input_size=(10, 3))


if __name__ == '__main__':
    train()

多分类交叉熵损失函数示例

1
2
3
4
5
6
7
8
9
10
11
12
13
# 标签, 表示样本0的真实类别是 0，样本1的真实类别是 1
# 标签通常是长整型，存储的是类别的索引，而不是one-hot编码
y_true = torch.tensor([0, 1], dtype=torch.long)
y_pred = torch.tensor([
    [2.0, 0.5, 0.1],  # 样本0：模型认为第0类分值最高
    [0.2, 3.1, 0.5]  # 样本1：模型认为第1类分值最高
])

# 交叉熵损失函数
criterion = nn.CrossEntropyLoss()
# 输出为所有样本损失的均值
loss = criterion(y_pred, y_true)
print(loss.item())     # 0.2192

二分类任务损失函数示例

1
2
3
4
5
6
7
8
9
10
# 在BCE损失中，标签必须是浮点数，形状与预测值一致
y_true = torch.tensor([[1.0], [0.0]], dtype=torch.float)
# 预测值
y_pred = torch.tensor([[2.5], [-1.2]])

# BCEWithLogitsLoss() = Sigmoid + nn.BCELoss()
# 如果用nn.BCELoss()，则要给输出层加上Sigmoid激活函数
criterion = nn.BCEWithLogitsLoss()
loss = criterion(y_pred, y_true)
print(loss.item())

回归任务损失函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
y_true = torch.tensor([2, 2, 2], dtype=torch.float)
y_pred = torch.tensor([1.9, 2.3, 4.5], dtype=torch.float)

# 平均绝对误差
criterion1 = nn.L1Loss()
loss = criterion1(y_pred, y_true)
print(loss.item())  # 0.9666666984558105

# 均方误差
criterion2 = nn.MSELoss()
loss = criterion2(y_pred, y_true)
print(loss.item())  # 2.116666555404663

# 平滑平均绝对误差
criterion3 = nn.SmoothL1Loss()
loss = criterion3(y_pred, y_true)
print(loss.item())  # 0.6833333373069763

神经网络优化

概念

  • Epoch：1个Epoch = 使用全部数据进行1轮训练
  • Batch_size：使用部分样本进行训练的样本数大小
  • 反向传播步骤：
    • 计算误差：在前向传播结束时，通过损失函数算出预测值和真实值的差距。
    • 梯度追踪：利用微积分中的链式求导法则，从后往前计算损失函数对每一个参数（权重W和偏置b）的导数（即梯度）。
    • 更新参数：优化器根据这些梯度，把参数往“误差变小”的方向推一小步
  • 指数加权平均：计算平均数时，每个数的权重不同，越远的数权重越小

梯度下降的优化

Momentum

在普通的 SGD 中，参数更新只取决于当前的梯度，可能会导致：

  1. 梯度来回震荡
  2. 在鞍点（导数为0的点）停住不更新

公式

  • 当前权重的更新不再只参考当前梯度，而是也参考之前的梯度
  • 越近的梯度权重越大
  • γ值越大，过去的梯度的影响越大，为0则等价于小批量梯度下降
  • 通过添加了一个正则项，解决了鞍点不更新的问题

AdaGrad

对频繁出现的特征进行用小学习率更新，偶尔出现的特征用大学习率更新

公式

步骤：

  1. 对每个权重，累计梯度的平方
  2. 在更新权重的时候，作为学习率的分母
  3. 这样频繁更新的权重学习率就小，偶尔更新的权重学习率就大
  4. 随着训练的进行，学习率会越来越小，做到前期大步探索，后期细微调整

缺点：后期学习率过小，更新缓慢

RMSProp

只记录最近一段时间的累计梯度，解决AdaGrad在后期学习率过小的问题

公式

步骤：

  1. 计算梯度平方的指数移动平均
  2. 使用指数移动平均来降低以前梯度的权重

✨Adam

Momentum优化梯度、RMSProp更新学习率

Adam是Momentum和RMSProp的结合

公式

  • 上面的公式是为了在开始训练时，解决指数移动平均还是0导致的更新慢问题
  • 刚开始训练轮次t很小，分母也小，就放大了整个值
  • 随着训练轮次t的增加，分母会逐渐趋于1，就不会继续放大

学习率衰减

在训练初期，模型离最优解很远，大的学习率可以更快向最优解收敛；

在训练后期，为了防止在两点间震荡，应当使用小的学习率

  • 等间隔衰减：每隔固定的epoch就衰减一次
  • 指定间隔衰减：在指定的训练轮次后衰减一次
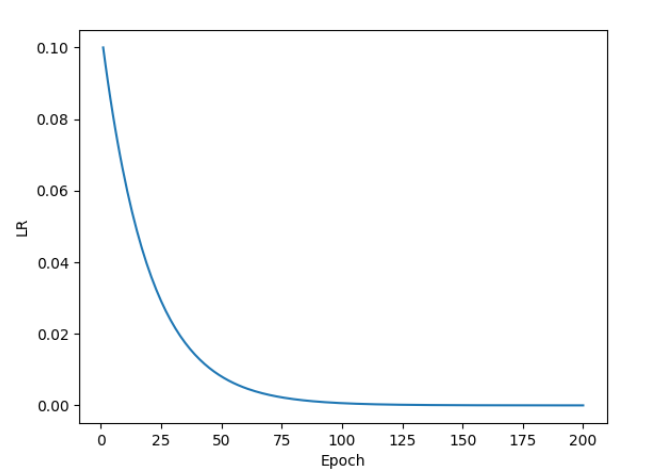
  • 按指数学习率衰减：让学习率随着训练轮数呈指数级减少

正则化

防止模型过拟合

Dropout正则化

Batch Normalization, BN，在神经网络的训练过程中，以一定的概率p（通常0.2~0.5），随机将一部分神经元的输出置为 0

通常放在激活函数后

训练阶段：按照概率p随机丢弃神经元，被丢弃的神经元在本批次中不会被更新

测试阶段：不丢弃任何神经元，因为训练时只用了一半神经元，测试时全用会导致输出数值偏大。因此，在训练时通常会输出 / (1 - p)来放大输出，从而保证测试时不需要做额外处理。

批量归一化

作用是确保每一层神经网络的输入始终保持稳定的分布

通常放在激活函数前

步骤：

  1. 计算这层神经元的输出的期望和方差

  2. 将输出处理成均值为0、方差为1的标准分布

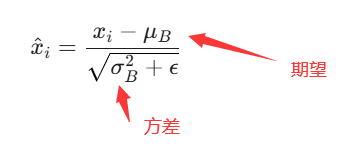
  3. 平移和缩放

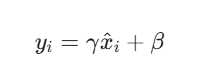
代码

动量法Momentum示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float)
# 优化器
optimizer = optim.SGD(params=[w], lr=0.01, momentum=0.9)

for _ in range(2):
    # 损失函数
    criterion = 0.5 * (w ** 2)

    # 反向传播
    optimizer.zero_grad()
    criterion.sum().backward()

    # 更新参数
    optimizer.step()

    print(f"权重: {w.item()}, 梯度: {w.grad}")
# 权重: 0.9900000095367432, 梯度: tensor([1.])
# 权重: 0.9711000323295593, 梯度: tensor([0.9900])

AdaGrad示例

1
2
3
4
5
# 同上，只改变优化器
optimizer = optim.Adagrad(params=[w], lr=0.01)

# 权重: 0.9900000095367432, 梯度: tensor([1.])
# 权重: 0.9829645752906799, 梯度: tensor([0.9900])

RMSProp示例

1
2
3
4
5
# 优化器，参数 alpha 就是指数移动平均里的平滑参数
optimizer = optim.RMSprop(params=[w], lr=0.01, alpha=0.99)

# 权重: 0.9000000357627869, 梯度: tensor([1.])
# 权重: 0.8329179883003235, 梯度: tensor([0.9000])

Adam示例

1
2
3
4
5
6
7
# 优化器
# betas：两个的平滑系数
# eps：让分母不为0
optimizer = optim.Adam(params=[w], lr=0.001, betas=(0.9, 0.999), eps=1e-08)

# 权重: 0.9990000128746033, 梯度: tensor([1.])
# 权重: 0.9980000257492065, 梯度: tensor([0.9990])

等间隔衰减示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 学习率，训练轮次，每轮的批次数
lr, epochs, iteration = 0.1, 200, 10

y_ture = torch.tensor([0])      # 标签
x = torch.tensor([1.0], dtype =torch.float) # 特征
w = torch.tensor([1.0], requires_grad=True) # 权重

# 优化器
optimizer = optim.SGD([w], lr=lr, momentum=0.9)

# 学习率调度器, 每step_size更新一次，每次为上个值的gamma倍
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)

# 记录轮次和学习率
lr_list = []

for _ in range(epochs):
    for _ in range(iteration):
        y_pred = w * x
        loss = (y_pred - y_ture) ** 2

        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    lr_list.append(scheduler.get_last_lr()[0])
    # 更新学习率
    scheduler.step()

plt.plot(range(1, len(lr_list) + 1), lr_list)
plt.xlabel('Epoch')
plt.ylabel('LR')
plt.show()

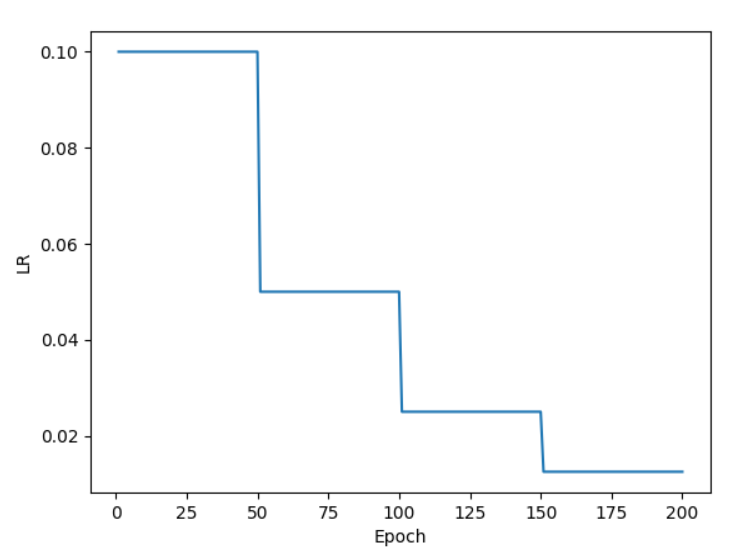
指定间隔衰减示例

1
2
# milestones: 指定间隔
scheduler = optim.lr_scheduler.MultiStepLR(optimizer, milestones = [75, 125, 175], gamma=0.5)

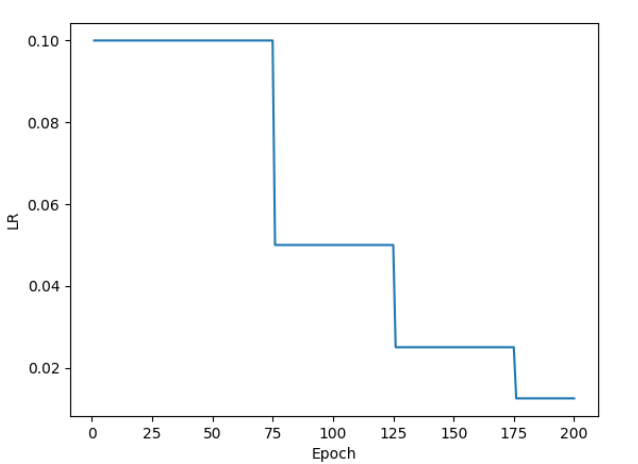
按指数学习率衰减示例

1
2
# gamma指数级递减
scheduler = optim.lr_scheduler.ExponentialLR(optimizer,gamma=0.95)

Dropout示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 输入的特征
t1 = torch.randint(0, 10, size=(1, 4)).float()
print(f"输入：{t1}")

# 一层神经元
linear1 = nn.Linear(4, 5)
l1 = torch.relu(linear1(t1))
print(f"经过第一层：{l1}")

# Dropout正则化
dropout = nn.Dropout(p=0.5)
d1 = dropout(l1)
print(f"随机丢弃后：{d1}")

# 输入：tensor([[8., 4., 3., 4.]])
# 经过第一层：tensor([[4.8319, 0.0000, 0.0000, 4.7008, 0.0000]], grad_fn=<ReluBackward0>)
# 随机丢弃并缩放后：tensor([[0.0000, 0.0000, 0.0000, 9.4017, 0.0000]], grad_fn=<MulBackward0>)

批量归一化示例

1
2
3
4
5
6
7
8
9
10
11
12
# 模拟图像，1张图像3个通道，每个通道都是3行4列的矩阵
input_2d = torch.randn(1, 3, 3, 4)
print(f"归一化前：{input_2d}")

# 专门为图像数据设计的归一化层
# num_features：图像通道数
# momentum：计算运行时的指数移动平均，与优化器的相反，running_mean = (1 - momentum) * running_mean + momentum * current_batch_mean
# affine：是否缩放平移
bn2d = nn.BatchNorm2d(num_features=3, eps=1e-5, momentum=0.1, affine=True)

output_2d = bn2d(input_2d)
print(f"归一化后：{output_2d}")

CNN

Convolutional Neural Network，卷积神经网络

实例代码

预测手机价格区间（多分类任务）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
import torch
from sklearn.preprocessing import StandardScaler
from torch.utils.data import TensorDataset  # 将数据转换成数据集
from torch.utils.data import DataLoader     # 数据加载器
from sklearn.model_selection import train_test_split
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import time
from torchsummary import summary

class PhonePriceModel(nn.Module):
    def __init__(self):
        super().__init__()

        self.linear1 = nn.Linear(in_features=20, out_features=128)
        self.linear2 = nn.Linear(in_features=128, out_features=256)
        self.linear3 = nn.Linear(in_features=256, out_features=4)

    def forward(self, x):
        x = torch.relu(self.linear1(x))
        x = torch.relu(self.linear2(x))
        # 多分类交叉熵损失函数自带了softmax，所以不需要再加上激活函数
        # x = torch.softmax(self.linear3(x), dim=1)
        x = self.linear3(x)

        return x

# 创建数据集
def create_dataset():
    data = pd.read_csv('./data/手机价格预测.csv')

    # 2000条数据, 21个特征
    print(f'形状：{data.shape}')
    print(f'{data.head()}')

    # 特征和标签
    x, y = data.iloc[:, :-1], data.iloc[:, -1]
    x = x.astype(np.float32)

    # 划分训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42, stratify=y)

    # 对数据进行标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    train_dataset = TensorDataset(torch.from_numpy(x_train), torch.tensor(y_train.values))
    test_dataset = TensorDataset(torch.from_numpy(x_test), torch.tensor(y_test.values))

    # 返回训练集，测试集，特征数，标签种类数
    return train_dataset, test_dataset, x.shape[1], len(np.unique(y))

# 训练模型
def train(train_dataset, input_dim, output_dim):
    # 创建数据加载器
    train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True)

    model = PhonePriceModel()
    # 将模型设置为训练模式
    model.train()

    # 损失函数
    criterion = nn.CrossEntropyLoss()

    # 优化器
    optimizer = optim.Adam(model.parameters(), lr=0.001)

    epochs = 50
    for epoch in range(epochs):
        total_loss, cnt = 0.0, 0
        for x, y in train_loader:
            y_pred = model(x)

            loss = criterion(y_pred, y)
            total_loss += loss

            # 反向传播
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            cnt += 1
        print(f'第 {epoch + 1}轮, 这轮的平均损失: {total_loss / cnt:4f}')

    # 只保存模型的参数，模型的结构不保存，导入时需要先创建个结构一模一样的模型
    torch.save(model.state_dict(), './model/PhonePriceModel.pth')

# 模型评估
def evaluate(test_dataset, input_dim, output_dim):
    # 加载保存的模型参数
    model = PhonePriceModel()
    state_dict = torch.load('./model/PhonePriceModel.pth')
    model.load_state_dict(state_dict)
    # 将模型设置为评估模式
    model.eval()

    # 测试集
    test_loader = DataLoader(test_dataset, batch_size=8, shuffle=False)

    # 预测对的数量
    correct = 0
    for x, y in test_loader:
        y_pred_tmp = model(x)
        # 返回张量中最大值的索引
        y_pred = torch.argmax(y_pred_tmp, dim=1)
        correct += (y == y_pred).sum().item()
    print(f'预测对的数量：{correct}, 准确率：{correct / len(test_dataset):4f}')


if __name__ == '__main__':
    train_dataset, test_dataset, input_dim, output_dim = create_dataset()
    # train(train_dataset, input_dim, output_dim)
    evaluate(test_dataset, input_dim, output_dim)
学习笔记 > AI
#AI
深度学习
http://xwww12.github.io/2025/12/31/AI/深度学习/
作者
xw
发布于
2025年12月31日
许可协议