机器学习

机器学习

概述

人工智能三大概念

  • 人工智能：AI，Artificial Intelligence
  • 机器学习：ML，Machine Learning
  • 深度学习：DL, Deep Learning

包含关系：人工智能 > 机器学习 > 深度学习

AI发展三要素

数据、算法、算力

样本、特征、标签

  • 样本(Sample)：一行数据就是一个样本；多个样本组成数据集；有时一条样本被叫成一条记录
  • 特征(feature) ：一列数据一个特征，有时也被称为属性
  • 标签/目标(label/target) ：模型要预测的那一列数据
  • 训练集(training set)：训练模型的数据集
  • 测试集(testing set)：测试模型的数据集，和训练集的比例一般为8:2或7:3

监督学习

  • 有监督学习：输入的训练数据有标签的

    • 分类问题：标签值是不连续的
    • 回归问题：标签值是连续的

  • 无监督学习：输入数据没有被标记，即样本数据类别未知，没有标签；

    根据样本间的相似性对样本集进行聚类

机器学习流程

  1. 获取数据

  2. 数据基本处理

    缺失值处理、异常值处理等

  3. 特征工程

    特征提取、预处理、降维等

  4. 模型训练

    线性回归、逻辑回归、决策树、GBDT等

  5. 模型评估

特征工程

  1. 特征提取
  2. 特征预处理：解决因量纲问题，导致有些特征对模型影响大、有些影响小
    • 归一化：（当前值 - 最小值）/（最大值 - 最小值）
    • 标准化
  3. 特征降维
  4. 特征选择
  5. 特征组合

机器学习库

KNN算法

K Nearest Neighbor，K邻近算法

思想

  1. 计算和样本的距离，找出最近的K个，按距离排序；
  2. 如果是分类问题，则这K个里哪种分类最多就为哪个（一样多选最近的）
  3. 如果是回归（预测）问题，则取这K个的均值

计算距离可以有多种方式，如欧式距离、曼哈顿距离等

K值选择

  • 过小会导致过拟合
  • 过大会导致欠拟合

代码实现

分类代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.neighbors import KNeighborsClassifier

# Classifier: 分类
x_train = [[0], [1], [2], [3]]  # 训练集特征
y_train = [0, 0, 1, 1]          # 训练集标签
x_test = [[5]]                  # 测试集特征

# 创建KNN分类模型对象
estimator = KNeighborsClassifier(n_neighbors=2)

# 训练
estimator.fit(x_train, y_train)

# 预测
y_pred = estimator.predict(x_test)
print(y_pred)

回归代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.neighbors import KNeighborsRegressor

# Regressor: 回归
x_train = [[0, 0, 1], [1, 1, 0], [3, 10, 10], [4, 11, 12]]  # 训练集特征
y_train = [0.1, 0.2, 0.3, 0.4]                              # 训练集标签
x_test = [[3, 11, 10]]                                      # 测试集特征

# 创建KNN回归模型
estimator = KNeighborsRegressor(n_neighbors=3)
# 模型训练
estimator.fit(x_train, y_train)

# 预测
y_pred = estimator.predict(x_test)
print(y_pred)

距离度量方式

  • 欧式距离：类似勾股定理，对应特征的差值平方，求和再开根号
  • 曼哈顿距离：abs(对应维度差值)之和
  • 切比雪夫距离：max(对应维度差值的的绝对值)

特征预处理

解决量纲问题导致放差值相差较大，影响模型的最终结果

  • 归一化：将值映射到指定区间里，容易受极值影响，适合小数据集

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    from sklearn.preprocessing import MinMaxScaler

    x_train = [[90, 2, 10, 40], [60, 4, 14, 45], [75, 3, 13, 46]]

    # 归一化对象, 默认[0, 1]
    scaler = MinMaxScaler(feature_range=(0, 1))

    # 进行归一化操作
    x_train_new = scaler.fit_transform(x_train)

    print(x_train_new)
     # [[1.         0.         0.         0.        ]
    #  [0.         1.         1.         0.83333333]
    #  [0.5        0.5        0.75       1.        ]]

  • 标准化：将数据转化为标准正态分布，可以减少极值的影响，适合大数据集

    (当前值 - 均值) / 标准差

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    from sklearn.preprocessing import StandardScaler

    x_train = [[90, 2, 10, 40], [60, 4, 14, 45], [75, 3, 13, 46]]

    # 标准化对象
    scaler = StandardScaler()

    # 进行标准化化操作
    x_train_new = scaler.fit_transform(x_train)

    print(x_train_new)
    # [[ 1.22474487 -1.22474487 -1.37281295 -1.3970014 ]
    #  [-1.22474487  1.22474487  0.98058068  0.50800051]
    #  [ 0.          0.          0.39223227  0.88900089]]

实例

鸢尾花分类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
from sklearn.datasets import load_iris                      #加载鸢尾花测试集的.
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split        #分割功练集和测试集的
from sklearn.preprocessing import StandardScaler            #数据标准化的
from sklearn.neighbors import KNeighborsClassifier          #KNN算法分类对象
from sklearn.metrics import accuracy_score                  # 模型评估


# 加载数据集
def dm01_load_iris():
    iris_data = load_iris()
    print(iris_data)            # 此数据集是字典形式的
    print(iris_data.data[:5])   # 数据集的特征
    print(iris_data.target[:5])   # 数据集的标签
    print(iris_data.feature_names) # 每列特征的意思
    print(iris_data.target_names) # 标签对应的意思

# 绘制散点图
def dm02_draw_iris():
    iris_data = load_iris()
    # 封装为DataFrame对象
    iris_df = pd.DataFrame(data=iris_data.data, columns=iris_data.feature_names)
    iris_df['target'] = iris_data.target
    # print(iris_df)
    # 绘制散点图
    sns.lmplot(data=iris_df, x='sepal length (cm)', y='sepal width (cm)', hue='target', fit_reg=False)
    plt.title('iris data')
    plt.show()

# 划分训练集和测试集
def dm03_split_train_test():
    iris_data = load_iris()
    # 按8:2的比例划分训练集和测试集, random_state: 随机种子
    x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=42)
    # print(len(x_train), len(x_test), len(y_train), len(y_test))

# 模型的评估和预测
def dm04_iris_evaluate_test():
    # 加载数据集
    iris_data = load_iris()
    # 切分为训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=42)
    # 数据预处理
    scaler = StandardScaler()
    x_train = scaler.fit_transform(x_train)     # 第一次进行标准化时，用fit_transform, 让scaler更契合数据集
    x_test = scaler.transform(x_test)           # 不是第一次进行标准化时, transform

    # 训练模型
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)

    # 模型预测
    y_pred = estimator.predict(x_test)                          # 对测试集进行预测
    print(f"测试集预测结果：{y_pred}")
    y_pred_custom = estimator.predict(scaler.transform([[7.8, 2.1, 3.9, 1.6]])) # 自定义的测试数据
    print(f"自定义数据预测结果：{y_pred_custom}")

    # 模型评估
    print(f"对训练集准确率: {estimator.score(x_train, y_train)}")    # 用训练集评估
    print(f"对测试集准确率: {accuracy_score(y_test, y_pred)}")       # 用测试集评估，比较标签和预测值


if __name__ == '__main__':
    dm04_iris_evaluate_test()

超参数选择方法

网格搜索

  • 交叉验证：

    1. 将训练集平均划分为N份（通常称N为折数），N - 1份作为训练集，1份作为验证集
    2. 每次拿不同的1份作为测试集，总共训练N次
    3. 将N轮得到的性能指标取平均值，这个平均值就是最终评估分数

  • 网格搜索：

    1. 将若干超参数可能得取值传递给网格搜索对象，会自动完成不同超参数的组合

      如超参数A可取值[0, 1, 2], 超参数B可取值[3, 4]

      则超参数的组合有3 * 2 = 6种

    2. 对每组超参数都采用交叉验证，最后选出最优的

      案例

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      from sklearn.datasets import load_iris                      #加载鸢尾花测试集的.
      from sklearn.model_selection import train_test_split, GridSearchCV        #分割功练集和测试集的
      from sklearn.preprocessing import StandardScaler            #数据标准化的
      from sklearn.neighbors import KNeighborsClassifier          #KNN算法分类对象
      from sklearn.metrics import accuracy_score                  # 模型评估


      # 加载数据集
      iris = load_iris()

      # 分割训练集和测试集
      x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)

      # 数据预处理
      scaler = StandardScaler()
      x_train = scaler.fit_transform(x_train)
      x_test = scaler.transform(x_test)

      # 模型
      estimator = KNeighborsClassifier()

      # 超参数可能的取值
      param_dict = {'n_neighbors': [i for i in range(1, 11)]}
      # cv: 交叉验证的折数, 返回处理后的模型
      estimator = GridSearchCV(estimator=estimator, param_grid=param_dict, cv=4)
      # 训练模型
      estimator.fit(x_train, y_train)
      print(f'最优评分: {estimator.best_score_}')
      print(f'最优超参组合: {estimator.best_params_}')
      print(f'最优的估计器对象: {estimator.best_estimator_}')
      print(f'具体的交叉验证结果: {estimator.cv_results_}')

手写数字识别

绘制数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split    # 分割数据集
from sklearn.neighbors import KNeighborsClassifier
import joblib                                           # 保存模型
from collections import Counter                         # 统计
from sklearn.metrics import accuracy_score              # 模型评估

# 根据索引画出对应的数字
def show_digit(idx):
    df = pd.read_csv('./data/手写数字识别.csv')
    if idx < 0 or idx >= len(df):
        print('索引越界')
        return
    # 第1列之后都为特征
    x = df.iloc[:, 1:]
    # 第0列为标签
    y = df.iloc[:, 0]
    # 将第idx行的784个灰度值重塑为28*28的形状
    x = x.iloc[idx].values.reshape(28, 28)
    # 根据灰度值绘制灰度图
    plt.imshow(x, cmap='gray')
    plt.axis('off')
    plt.show()

训练和保存模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def train_model():
    df = pd.read_csv('./data/手写数字识别.csv')
    x = df.iloc[:, 1:]
    y = df.iloc[:, 0]
    # 数据预处理
    x = x / 255
    # 划分训练集和测试集, stratify: 让每个划分的集合的y更均匀
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42, stratify=y)

    # 模型训练
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)

    # 模型评估
    print(f'准确率: {estimator.score(x_test, y_test)}')
    print(f'准确率: {accuracy_score(y_test, estimator.predict(x_test))}')
    joblib.dump(estimator, './model/手写数字识别.pkl')    # pickle, 后缀用pkl/pth/pickle都行
    print("保存成功")

使用保存的模型

1
2
3
4
5
6
7
8
9
def use_model():
    # 用来测试的图片(28 * 28)
    img = plt.imread("./data/demo.png")
    img = img.reshape(1, -1)    # 第二个数为-1时表示展平，不需要再归一化，imread时自动做了
    # 加载保存的模型
    estimator = joblib.load('./model/手写数字识别.pkl')
    # 使用
    y_pred = estimator.predict(img)
    print(y_pred)

线性回归

用线性公式来描述多个自变量（特征）和一个因变量（标签）之间的关系

属于有监督学习，标签是连续的

概念

  • 一元线性回归：y = wx + b（w为权重，b为偏置），目标值与单个因变量有关
  • 多元线性回归：y = (w1x1 + b1) + (w2x2 + b2) + … + b，目标值与多个因变量有关

目标是找出能使损失函数最小的权重和偏置

损失函数

Loss Function, 用来评判模型的好坏，值越小表示误差越小

损失函数种类

  • 均方误差（MSE）：(预测值 - 真实值)^2求和 / 样本总数
  • 平均绝对误差（MAE）：|预测值 - 真实值|求和 / 样本总数
  • 均方根误差（RMSE）：均方误差的值开根号

找让损失函数最小的权重和偏置的方法

最小二乘法

最小二乘法可以直接计算出最优的w和b，前提是数据量不大，且方程有解析解

  • 一元线性回归的情况：

    1. 损失函数分别对w（权重）和b（偏置）分别求偏导
    2. 然后联立起来求偏导为0的值，来让损失函数最小

  • 多元线性回归的情况：

    1. 多元线性回归方程式：y = w1x1 + w2x2 + w3x3 + … + b = w^Tx + b
    2. 把一个样本的特征值带入x1、x2、….得预测值
    3. 损失函数 = 累加每个样本的（真实值 - 预测值）^ 2

    1. 对损失函数的w（包含所有权重的矩阵）求导，得到方程

      X为所有特征方程组成的矩阵

    2. 可知要求w时X^(-1)要存在，不是所有情况都能用

✨梯度下降法

沿着梯度下降的方向求解极小值

  • 一元线性回归的情况：

    1. 随机初始化 w 和 b，确定一个学习率α，选择迭代次数
    2. 在每一步迭代中，使用当前 w 和 b 计算损失函数对 w 和 b 的偏导数（梯度）
    3. 沿梯度的反方向更新w和b（梯度的方向是上升最快的方向）
    4. 直到迭代了设置的迭代次数、或者损失函数收敛到了指定的阈值内时停止

  • 多元线性回归的情况：

    对所有的参数求偏导，然后同时更新

梯度下降法例子

梯度下降法分类

根据每轮迭代中用于计算梯度的样本数量来分类

  • 批量梯度下降法(Batch(Full) Gradient Descent, BGD/FGD)

    定义：使用全部训练数据来计算损失函数的梯度

    优点：能保证收敛到全局最优解

    缺点：速度慢，内存占用大

  • 随机梯度下降法 (Stochastic Gradient Descent, SGD)

    定义： 每次参数更新时，只使用随机的一个训练样本来计算梯度

    优点：计算速度快

    缺点：收敛性较差，通常只能震荡地接近最优解

  • ✨小批量梯度下降法 (Mini-Batch Gradient Descent, MBGD)

    定义：每次参数更新时，使用一小批（Mini-Batch）训练样本（通常是 32、64、128 等）来计算梯度

    优点：结合和BGD和SGD的特点

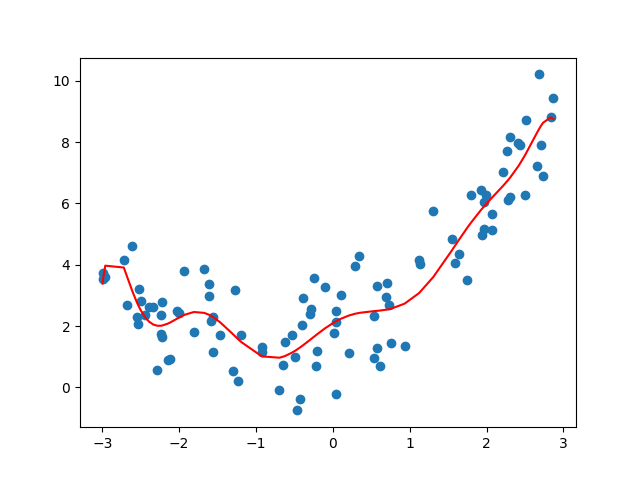
欠拟合和过拟合的解决方法

欠拟合的成因：学习到数据的特征过少

欠拟合的解决方法：添加特征、添加多项式特征项

过拟合的成因：特征过多，存在一些嘈杂特征

过拟合的解决方法：重新清洗数据、增大数据量、正则化、减少特征数量

正则化

过拟合时，模型往往会给某些特征极大的权重、专门去迎合训练数据中的噪声

正则化的作用是让权重的值不要太大

L1正则化

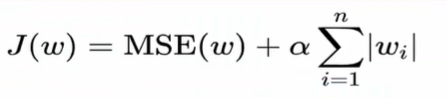
  • α为惩罚系数，即权重大的时候对损失函数的影响
  • 可能会让一些权重值直接变成0（在特征很多需要降维时使用）

L2正则化

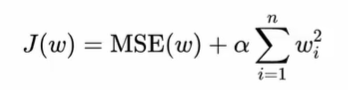
  • 对权重的调整更平滑一些，一般不会变为0

代码

正规方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from sklearn.preprocessing import StandardScaler    # 特征处理
from sklearn.model_selection import train_test_split # 数据集划分
from sklearn.linear_model import LinearRegression   # 正规方程的回归模型
from sklearn.linear_model import SGDRegressor       # 梯度下降的回归模型
from sklearn.metrics import mean_squared_error, root_mean_squared_error, mean_absolute_error  # 评估

import pandas as pd
import numpy as np

# 数据集
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])  # 特征
target = raw_df.values[1::2, 2]     # 标签

# 切分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=42)

# 预处理
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

# 线性回归的正规方程模型, fit_intercept: 是否要有偏置
estimator = LinearRegression(fit_intercept=True)
estimator.fit(x_train, y_train)

print(f"权重：{estimator.coef_}")
print(f"偏置：{estimator.intercept_}")

# 预测
y_pred = estimator.predict(x_test)
print(f"预测结果：{y_pred}")

# 评估
# MSE：均方误差
print("均方误差: ", mean_squared_error(y_test, y_pred))
# RMSE：均方根误差
print("均方根误差: ", root_mean_squared_error(y_test, y_pred))
# MAE：平均绝对误差
print("平均绝对误差: ", mean_absolute_error(y_test, y_pred))

梯度下降法

1
2
3
# 将上面代码的模型换成随机梯度下降的SGDRegressor即可
# learning_rate: 学习率为常数, eat0: 学习率
estimator = SGDRegressor(fit_intercept=True, learning_rate="constant", eta0=0.01)

欠拟合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def demo_01():
    # 指定随机种子，让每次随机数固定
    np.random.seed(23)
    # 随机生成100格随机数当做特征
    x = np.random.uniform(-3, 3, size=100)
    X = x.reshape(-1, 1)
    # 随机生成100格随机数当做标签
    y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

    estimator = LinearRegression()
    estimator.fit(X, y)
    y_pred = estimator.predict(X)

    # 均方误差评估
    print(f"均方误差: {mean_squared_error(y, y_pred)}")

    # 绘图
    plt.scatter(x, y)   # 散点图（真实值）
    plt.plot(x, y_pred, color='red')    # 折线（预测值）
    plt.show()

拟合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def demo_02():
    # 指定随机种子，让每次随机数固定
    np.random.seed(23)
    # 随机生成100格随机数当做特征
    x = np.random.uniform(-3, 3, size=100)
    X1 = x.reshape(-1, 1)
    X2 = np.hstack([X1, X1 ** 2])   # 行拼接
    # 随机生成100格随机数当做标签
    y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

    estimator = LinearRegression()
    estimator.fit(X2, y)
    y_pred = estimator.predict(X2)

    # 均方误差评估
    print(f"均方误差: {mean_squared_error(y, y_pred)}")

    # 绘图
    plt.scatter(x, y)  # 散点图（真实值）
    plt.plot(np.sort(x), y_pred[np.argsort(x)], color='red')  # 折线（预测值）
    plt.show()

过拟合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def demo_03():
    # 指定随机种子，让每次随机数固定
    np.random.seed(23)
    # 随机生成100格随机数当做特征
    x = np.random.uniform(-3, 3, size=100)
    X1 = x.reshape(-1, 1)
    X2 = np.hstack([X1, X1 ** 2, X1 ** 3, X1 ** 4, X1 ** 5, X1 ** 6, X1 ** 7, X1 ** 8, X1 ** 9, X1 ** 10])  # 行拼接
    # 随机生成100格随机数当做标签
    y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

    estimator = LinearRegression()
    estimator.fit(X2, y)
    y_pred = estimator.predict(X2)

    # 均方误差评估
    print(f"均方误差: {mean_squared_error(y, y_pred)}")

    # 绘图
    plt.scatter(x, y)  # 散点图（真实值）
    plt.plot(np.sort(x), y_pred[np.argsort(x)], color='red')  # 折线（预测值）
    plt.show()

正则化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 正则化
def demo_04():
    # 指定随机种子，让每次随机数固定
    np.random.seed(23)
    # 随机生成100格随机数当做特征
    x = np.random.uniform(-3, 3, size=100)
    X1 = x.reshape(-1, 1)
    X2 = np.hstack([X1, X1 ** 2, X1 ** 3, X1 ** 4, X1 ** 5, X1 ** 6, X1 ** 7, X1 ** 8, X1 ** 9, X1 ** 10])  # 行拼接
    # 随机生成100格随机数当做标签
    y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

    # alpha: 惩罚系数
    estimator = Lasso(alpha=0.01)	# L1正则化
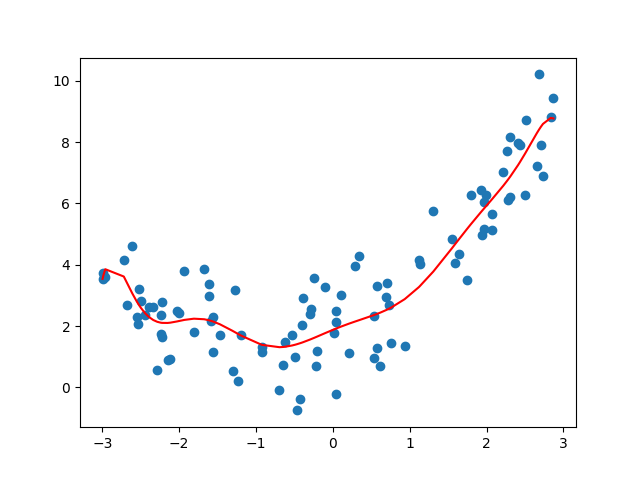
    # estimator = Ridge(alpha=1)		# L2正则化
    estimator.fit(X2, y)
    y_pred = estimator.predict(X2)

    # 均方误差评估
    print(f"均方误差: {mean_squared_error(y, y_pred)}")

    # 绘图
    plt.scatter(x, y)  # 散点图（真实值）
    plt.plot(np.sort(x), y_pred[np.argsort(x)], color='red')  # 折线（预测值）
    plt.show()

L1正则化

L2正则化

逻辑回归

有监督学习，标签是离散的

概念

  • 逻辑回归的作用：分类

  • Sigmoid激活函数：

    公式

    图像

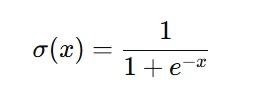
    作用：把数映射到[0, 1]区间上，来表示样本属于某一类的概率

  • 最大似然估计：找一组参数，让已经发生的这些数据在这个模型下看起来最合理、最有可能发生

损失函数

  • 如果y标签为1，则只会计算函数左边那块
  • 如果y标签为0，则只会计算函数右边那块
  • 注意到前面有个符号，则概率值越大，损失函数越小

分类的评估方法

使用准确率来评估太粗糙了，正类和负类同等重要，错一次的代价是一样的；

准确率看不出来预测错的类型是什么，

例如预测是否生病，1000个人中只有一个人真生病，模型只会输出没生病，准确率就高达99.9%

混淆矩阵

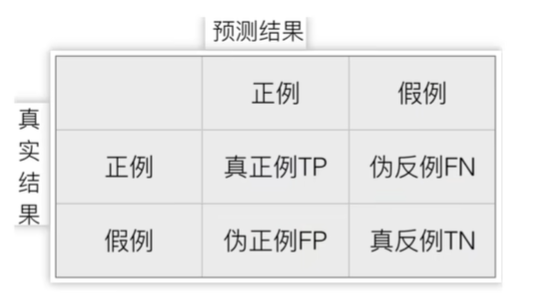
  • 精确率：TP / (TP + FP)，预测结果为正中，对的占比
  • 召回率：TP / (TP +FN)，正例中被预测为正的占比
  • F1-score：2 * 精确率 * 召回率 / (精确率 + 召回率)

代码

逻辑回归实例1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression     # 逻辑回归模型
from sklearn.preprocessing import StandardScaler        # 数据预处理
from sklearn.model_selection import train_test_split    # 数据划分
from sklearn.metrics import accuracy_score              # 评估


# 数据集, 空值以?表示
data = pd.read_csv('./data/breast-cancer-wisconsin.csv')

# 将?替换成nan, 直接修改原数据
data.replace(to_replace='?', value=np.nan, inplace=True)

# 删除有nan的行
data.dropna(axis=0, inplace=True)

# 特征, 前闭后开
x = data.iloc[:, 1:-1]
# 标签
y = data.iloc[:, -1]

# 划分训练集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 训练
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

# 预测
y_pred = estimator.predict(x_test)
print(f"准确率：{accuracy_score(y_test, y_pred)}")

混淆矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import pandas as pd
from sklearn.metrics import confusion_matrix, precision_score, recall_score, f1_score

# 模拟标签
y_train = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性', '良性', '良性', '良性']

# 模拟A模型的预测值
y_pred_A = ['恶性', '恶性', '恶性', '良性', '良性', '良性', '良性', '良性', '良性', '良性']

# 模拟B模型的预测值
y_pred_B = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性']

# 正例，反例
label = ['恶性', '良性']

cm_A = confusion_matrix(y_train, y_pred_A, labels=label)
pd_A = pd.DataFrame(cm_A, index=label, columns=label)
print(f'混淆矩阵A：\n{pd_A}')
print(f'精确率A：{precision_score(y_train, y_pred_A, pos_label="恶性")}')
print(f'召回率率A：{recall_score(y_train, y_pred_A, pos_label="恶性")}')
print(f'f1-scoreA：{f1_score(y_train, y_pred_A, pos_label="恶性")}')


cm_B = confusion_matrix(y_train, y_pred_B, labels=label)
pd_B = pd.DataFrame(cm_B, index=label, columns=label)
print(f'混淆矩阵B：\n{pd_B}')
print(f'精确率B：{precision_score(y_train, y_pred_B, pos_label="恶性")}')
print(f'召回率率B：{recall_score(y_train, y_pred_B, pos_label="恶性")}')
print(f'f1-scoreB：{f1_score(y_train, y_pred_B, pos_label="恶性")}')

逻辑回归实例2

one hot编码：为每个类别创建一个独立的二进制特征列，用 1 表示样本属于该类别，用 0 表示不属于。比如把颜色拆分为是否为红色，是否为绿色，是否为蓝色；

作用：适配机器学习算法, 若直接类别1=1、类别2=2、类别3=3，模型可能会误认为类别3 > 类别2 > 类别1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression     # 逻辑回归模型
from sklearn.model_selection import train_test_split    # 数据划分
from sklearn.metrics import confusion_matrix, precision_score, recall_score, f1_score, accuracy_score, \
    classification_report


# 数据读取和预处理
def dm01_data_preprocessing():
    churn_df = pd.read_csv('./data/churn.csv')
    # one hot编码, 把Churn和gender拆开
    churn_df = pd.get_dummies(churn_df, ['Churn', 'gender'])
    churn_df.drop(['Churn_No', 'gender_Female'], axis=1, inplace=True)
    churn_df.rename(columns={'Churn_Yes': 'flag'}, inplace=True)    # Churn_Yes为标签
    return churn_df

# 数据可视化，查看每月留存和流失的用户数
def dm02_data_visualization():
    churn_df = dm01_data_preprocessing()
    # Index(['Partner_att', 'Dependents_att', 'landline', 'internet_att',
    #        'internet_other', 'StreamingTV', 'StreamingMovies', 'Contract_Month',
    #        'Contract_1YR', 'PaymentBank', 'PaymentCreditcard', 'PaymentElectronic',
    #        'MonthlyCharges', 'TotalCharges', 'flag', 'gender_Male'],
    #       dtype='object')
    sns.countplot(x='Contract_Month', data=churn_df, hue='flag')
    plt.show()

def dm03_logistic_regression():
    churn_df = dm01_data_preprocessing()
    # 提取特征
    x = churn_df[['Contract_Month', 'internet_other', 'PaymentElectronic']]
    # 提取标签
    y = churn_df['flag']
    # 划分训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

    # 训练模型
    estimator = LogisticRegression()
    estimator.fit(x_train, y_train)

    y_pred = estimator.predict(x_test)

    print(f'准确率: {accuracy_score(y_test, y_pred)}')
    print(f'精确率：{precision_score(y_test, y_pred)}')
    print(f'f1-score: {f1_score(y_test, y_pred)}')
    print(f'分类评估报告: {classification_report(y_test, y_pred)}')

if __name__ == '__main__':
    dm03_logistic_regression()

决策树

概念

什么是决策树：树中每个非叶子节点表示一个特征上的判断，每个分支表示一个判断结果的输出，每个叶子节点代表一种分类结果

建立决策树过程：

  1. 特征选择：选取有较强分类能力的特征
  2. 生成决策树
  3. 剪枝：解决过拟合问题

种类

ID3决策树

偏向于选择种类多的特征

概念

  • 信息熵计算方法：-Σ(标签分类占比)*log(标签分类占比)

  • 信息熵越大代表越混乱

  • 条件熵计算方法：在已知特征 X 的条件下，目标变量 Y 的不确定性

    条件熵计算方法

  • 信息增益 = 信息熵 - 条件熵

建树过程

  1. 计算每个特征的信息增益
  2. 使用信息增益最大的特征，将该数据集拆分为多个子集
  3. 使用该特征值作为决策树的一个节点
  4. 对每个子集，使用剩余的特征重复上述过程
  5. 当这个分支的所有数据都只有一个标签时，这个分支终止，叶子结点为这个标签

C4.5决策树

解决ID3决策树过拟合的问题

ID3决策树偏向于选择种类多的特征，而信息增益率偏向于选择种类少的特征

概念

  • 特征熵：算特征列的熵
  • 信息增益率=信息增益 / 特征熵

建树过程

和ID3树类似，只是将信息增益换成信息增益率

CART决策树

Classification and Regression Tree，分类与回归树，最常用的决策树算法之一，核心特点是既能做分类任务，也能做回归任务

概念

  • 基尼值：从数据集中随机抽取两个样本，类别标记不一致的概率

    基尼值公式

    • 基尼值越小，节点的纯度越高

  • 基尼指数：一个特征中，Σ(某个取值对应的基尼值 * 这种取值的占比)

✨分类树建树过程

  1. CARF要求每个节点做二分划分,分别分析所有特征的所有可能划分

    如果特征值是连续的，将数值做升序排序，以相邻值的中点作为二分位置

  2. 计算划分后的Gini指数

  3. 选择最小值对应的特征的划分

  4. 下一次节点分裂时，和前面的决策树不同，用过的特征仍然可以再用

建树例子

回归树建树过程

  1. 分裂依据是最小化节点分裂后的总平方误差（MSE）
  2. 节点的MSE就是每个样本的真实值和节点均值的误差平方和
  3. 分裂点的选择为，将某个特征的特征值按升序排序，每两个值的中间值选为分裂点
  4. 遍历所有特征和该特征可能的阈值，选择MSE最小的组合来进行分裂

预测

将样本沿着树的分叉走，直到到达叶子结点。

如果是分类问题：叶子节点所有样本的标签中，最多的即作为预测值

如果是回归问题：叶子节点所有样本的标签的均值即作为预测值

剪枝

  • 预剪枝：在划分前进行估计，如果不能带来决策树泛化能力提升，则停止划分
    • 优点：降低了过拟合的风险，减少了决策树的训练时间
    • 缺点：带来了欠拟合的风险
  • 后剪枝：训练完后，自底向上对非叶子节点进行考察，若将该节点替换为叶子结点能提升泛化能力，则替换
    • 优点：泛化能力优于预剪枝
    • 缺点：训练开销大得多

代码

分类决策树案例

数据集下载：https://tianchi.aliyun.com/dataset/179968

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import pandas as pd
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier     # 决策树
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

def titanic_data(file_path):
    titanic_train_df = pd.read_csv(file_path)
    # 特征：仓位等级，年龄，性别
    x = titanic_train_df[['Pclass', 'Age', 'Sex']]
    # 标签：是否存活
    try:
        y = titanic_train_df['Survived']
    except KeyError:
        y = pd.Series()
    x = x.copy()    # 解决警告
    # 将年龄的空值赋值为年龄的均值
    x['Age'] = x['Age'].fillna(x['Age'].mean())
    # 将性别拆分
    x = pd.get_dummies(x, columns=['Sex'])
    return x, y

def plot(estimator):
    plt.figure(figsize = (30, 40))      # 设置图片大小
    plot_tree(decision_tree=estimator, max_depth=10, filled=True)
    plt.savefig('./data/titanic_tree.png')

def titanic():
    x, y = titanic_data('./data/titanic_train.csv')
    x_vail, _ = titanic_data('./data/titanic_test.csv')
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

    # 训练
    # criterion: 建树的方式，默认gini; max_depth: 树的最大深度;
    # min_samples_split: 节点分裂需要的最小样本数; min_samples_leaf: 分裂后叶子中要包含的最小样本数; 这两个如果不满足就不会分裂
    estimator = DecisionTreeClassifier(max_depth=10)
    estimator.fit(x_train, y_train)

    # 预测
    y_pred = estimator.predict(x_test)

    # 评估
    print(f'评估报告{metrics.classification_report(y_test, y_pred)}')

    # 绘制决策树
    plot(estimator)


if __name__ == '__main__':
    # x_train, y_train = titanic_data('./data/titanic_train.csv')
    titanic()

回归决策树案例

回归用的较多的还是线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor      # 回归决策树
from sklearn.linear_model import LinearRegression   # 线性回归
import matplotlib.pyplot as plt

x_train = np.array(list(range(1, 11))).reshape(-1, 1)
y_train = np.array([5.56, 5.7, 5.91, 6.4, 6.8, 7.05, 8.9, 8.7, 9, 9.05])
x_test = np.arange(0, 10, 0.1).reshape(-1, 1)

# 三种模型
estimator1 = LinearRegression()
estimator2 = DecisionTreeRegressor(max_depth=2)
estimator3 = DecisionTreeRegressor(max_depth=3)

estimator1.fit(x_train, y_train)
estimator2.fit(x_train, y_train)
estimator3.fit(x_train, y_train)

y_pred1 = estimator1.predict(x_test)
y_pred2 = estimator2.predict(x_test)
y_pred3 = estimator3.predict(x_test)

# 画图比较区别
plt.scatter(x_train, y_train, color='gray')     # 散点图
plt.plot(x_test, y_pred1, color='red', label='Linear Regression')
plt.plot(x_test, y_pred2, color='blue', label='max_depth=2')
plt.plot(x_test, y_pred3, color='green', label='max_depth=3')
plt.show()

集成学习

通过多个模型的组合形成一个精度更高的模型

训练时，使用训练集依次训练出弱学习器，对未知的样本进行预测

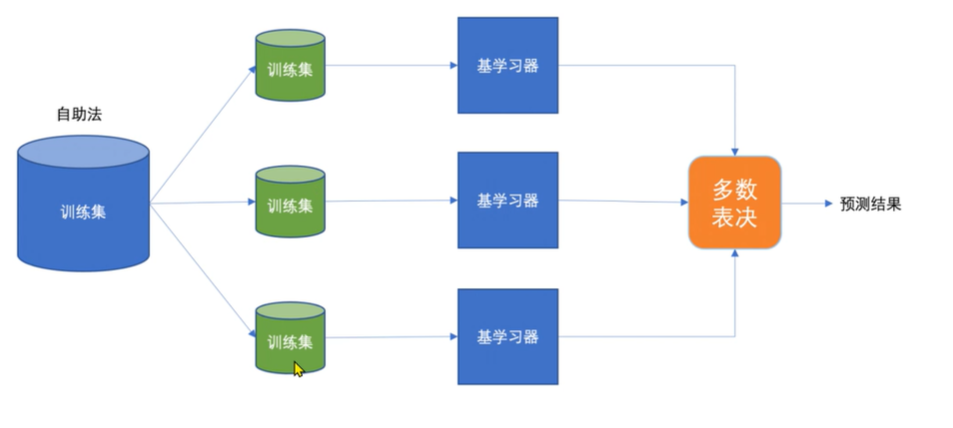
并行式集成（Bagging）

训练过程：

  1. 从原始数据集中，通过自助采样（有放回地随机选样本）生成多个不同的子数据集。
  2. 用每个子数据集训练一个独立的基模型（比如决策树）。
  3. 最终预测时，分类问题取多数投票，回归问题取平均值。

随机森林算法

  1. 每次有放回的抽取若干个样本
  2. 选取部分特征来学习，默认是CART树
  3. 构建多颗这样的树

串行式集成（Bossting）

训练过程：

  1. 先训练一个基模型，对样本进行预测。
  2. 提高预测错误的样本的权重，让下一个基模型重点学习这些难样本。
  3. 重复上述过程，生成多个基模型，最终按权重融合

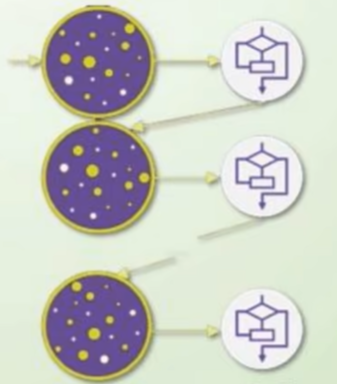
Adaboost算法

  1. 开始时所有样本权重相同，模型会优先拟合权重高的样本

    权重在算当前错误率的时候用，若某个样本预测错了，错误率就会加上这个权重

    因此会尽量先拟合权重高的样本

  2. 共训练T轮，每轮都用到全部训练集，T为学习器（仅包含一个分裂节点的决策树）的数量，每个学习器也有权重

  3. 每轮训练后，预测错误的样本权重会升高，对的会降低，权重会传给下一个学习器

  4. 最后将这些学习器合成一个强模型，通过加权投票来给出结果

GDBT算法

Gradient Boosting Decision Tree，梯度提升决策树

逐步拟合前一轮模型的残差

以回归为例

  1. 初始化弱学习器：取(训练时的)标签的均值为预测值，使初始损失最小

    1. 找到使得负梯度（目标值 - 预测值）均方误差最小的切分点，将样本分到两个叶子结点中
    2. 预测时根据特征值判断到哪个叶子接点中，预测值为样本标签的均值

  2. 将上一轮的负梯度（残差）作为下一轮的标签，继续重复上面的操作

  3. 训练完后，预测时是把测试集给每个弱学习器，累加每个的输出值即为预测值

XGBoost算法

eXtreme Gradient Boosting，极端梯度提升

在 GBDT 的基础上，增加了正则化项，用于约束模型复杂度，避免过拟合

正则化项

  1. 初始化模型

  2. 迭代训练弱决策树

    • 计算当前模型的一阶导数和二阶导数，作为拟合目标；

    • 基于特征并行优化，为当前决策树寻找最优分裂点）；

    • 生成新的弱决策树，并通过正则化项约束树的复杂度；

      只有分裂后损失值下降的足够多才允许分裂；还会尽量选择多个小权重叶节点，而非少数大权重叶节点

    • 确定该树的权重，将其加入强模型，更新整体预测结果。

  3. 有弱树加权累加后，得到最终强模型

代码

随机森林实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import pandas as pd
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier     # 决策树
from sklearn.ensemble import RandomForestClassifier # 随机森林算法
from sklearn.model_selection import GridSearchCV

titanic_train_df = pd.read_csv('./data/titanic_train.csv')
# 特征：仓位等级，年龄，性别
x = titanic_train_df[['Pclass', 'Age', 'Sex']].copy()
# 标签：是否存活
y = titanic_train_df['Survived']
# 将年龄的空值赋值为年龄的均值
x['Age'] = x['Age'].fillna(x['Age'].mean())
# 将性别拆分
x = pd.get_dummies(x, columns=['Sex'])

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

estimator1 = DecisionTreeClassifier()
estimator1.fit(x_train, y_train)

print(estimator1.score(x_test, y_test))   # 0.8778089887640449

# 随机森林
estimator2 = RandomForestClassifier()
# 网格搜索来选择超参数
parser = {'n_estimators': [90, 130, 150, 170], 'max_depth': [2, 4, 5, 7]}
gs_estimator = GridSearchCV(estimator=estimator2, param_grid=parser, cv=3)
gs_estimator.fit(x_train, y_train)

print(gs_estimator.score(x_test, y_test))
print(gs_estimator.best_params_)

Adaboost算法实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import pandas as pd
from sklearn.preprocessing import LabelEncoder          # 标签编码器
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score


wine_df = pd.read_csv('./data/wine0501.csv')

# 标签有三个值，但是决策树是二叉树只能二分类，因此过滤掉其中一个值
wine_df = wine_df[wine_df['Class label'] != 1]

x = wine_df[['Alcohol', 'Hue']]     # 特征
y = wine_df['Class label']          # 标签

# LabelEncoder用于对离散的类别型标签进行“类别→整数”的映射转换
# 将标签从[2, 3] -- > [0, 1]
y = LabelEncoder().fit_transform(y)

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y)

# 单一决策树
estimator1 = DecisionTreeClassifier(max_depth=1)
estimator1.fit(x_train, y_train)
y_pred1 = estimator1.predict(x_test)
print(accuracy_score(y_test, y_pred1))

# Adaboost算法
# 指定学习器及数量
estimator2 = AdaBoostClassifier(estimator=estimator1, n_estimators=200, learning_rate=0.1)
estimator2.fit(x_train, y_train)
y_pred2 = estimator2.predict(x_test)
print(accuracy_score(y_test, y_pred2))

GBDT算法实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import pandas as pd
from sklearn.preprocessing import LabelEncoder          # 标签编码器
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score


titanic_train_df = pd.read_csv('./data/titanic_train.csv')
# 特征：仓位等级，年龄，性别
x = titanic_train_df[['Pclass', 'Age', 'Sex']].copy()
# 标签：是否存活
y = titanic_train_df['Survived']
# 将年龄的空值赋值为年龄的均值
x['Age'] = x['Age'].fillna(x['Age'].mean())
# 将性别拆分
x = pd.get_dummies(x, columns=['Sex'])

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

# 梯度提升决策树
estimator = GradientBoostingClassifier()
param_dict = {
    'n_estimators': [100, 120],
    'learning_rate': [0.1, 0.2],
    'max_depth': [3, 5, 7],
}
gs_estimator = GridSearchCV(estimator=estimator, param_grid=param_dict)
gs_estimator.fit(x_train, y_train)

y_pred = gs_estimator.predict(x_test)
print(accuracy_score(y_pred, y_test))

XGBoost算法实例

需要安装pip install xgboost

官网：https://xgboost.readthedocs.io/en/stable/index.html

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import joblib               # 保存和加载模型
import numpy as np
import pandas as pd
import xgboost as xgb
from collections import Counter     # 统计数据
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import classification_report
from sklearn.model_selection import StratifiedKFold     # 分层K折交叉验证
from sklearn.utils import class_weight      # 平衡权重


# 将原始数据切分成训练集和测试集并保存
def process_data():
    df = pd.read_csv('./data/红酒品质分类.csv')
    # 最后一列是标签，前面的都是特征
    x = df.iloc[:, :-1]
    # 标签范围为[3, 8], 预处理成[0, 5]
    y = df.iloc[:, -1] - 3

    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42, stratify=y)

    pd.concat([x_train, y_train], axis=1).to_csv('./data/红酒品质分类_train.csv', index=False)
    pd.concat([x_test, y_test], axis=1).to_csv('./data/红酒品质分类_test.csv', index=False)

# 训练并保存模型
def train_model():
    train_data = pd.read_csv('./data/红酒品质分类_train.csv')
    test_data = pd.read_csv('./data/红酒品质分类_test.csv')

    x_train = train_data.iloc[:, :-1]
    y_train = train_data.iloc[:, -1]
    x_test = test_data.iloc[:, :-1]
    y_test = test_data.iloc[:, -1]

    # 网格搜索选超惨
    param_dict = {
        'max_depth': [2, 3, 5, 6, 7],
        'n_estimators': [100, 150],
        'learning_rate': [0.1, 0.2, 0.3],
    }
    # 折数，是否打乱数据
    skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=23)
    # 因为数据集的标签不均衡，使用这个平衡权重
    sample_weight = class_weight.compute_sample_weight('balanced', y_train)

    # 设置模型使用GPU来训练
    estimator = xgb.XGBClassifier(
        tree_method='hist',
        device='cuda',
        objective='multi:softprob',
        num_class=6,
        eval_metric='mlogloss',
        n_jobs=1,
        random_state=42
    )
    gs_estimator = GridSearchCV(estimator, param_grid=param_dict, cv=skf)
    gs_estimator.fit(x_train, y_train, sample_weight=sample_weight)

    print(gs_estimator.best_params_)
    print(gs_estimator.score(x_test, y_test))
    # 保存训练好的模型
    joblib.dump(gs_estimator, './model/红酒品质分类.pkl')

if __name__ == '__main__':
    train_model()

朴素贝叶斯算法

朴素贝叶斯是有监督的分类算法，它的本质是：利用贝叶斯公式，结合「特征独立」的朴素假设，计算样本属于每个类别的后验概率，最终选择概率最大的那个类别作为预测结果。

原理

朴素贝叶斯基于条件概率公式：

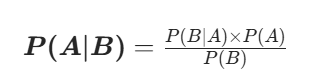
条件概率公式

朴素的含义是：特征之间是互相独立的

预测步骤：

  1. 通过分词器提取样本中关键字作为特征
  2. 根据概率公式，计算在有这些特征的条件下，是某个标签的概率
  3. 取概率最大的标签作为预测值

代码

贝叶斯算法实例

安装分词器：pip install jieba

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import jieba            # 分词器
from sklearn.feature_extraction.text import CountVectorizer # 词频统计
from sklearn.metrics import accuracy_score
from sklearn.naive_bayes import MultinomialNB   # 贝叶斯模型

# 含有中文，编码格式要用gbk
df = pd.read_csv('./data/书籍评价.csv', encoding='gbk')

# 标签列
y = np.where(df['评价'] == '好评', 1, 0)

# 分词，并且将分好的词用,拼接起来
comment_list = [','.join(jieba.lcut(line)) for line in df['内容']]

# 评论中没有用的词
with open('./data/stopwords.txt', 'r', encoding='utf-8') as f:
    stop_words_list = [line.strip() for line in f.readlines()]
    stop_words_list = list(set(stop_words_list))    # 去重

# 从评论词中删去停用词,并且统计词频
transfer = CountVectorizer(stop_words=stop_words_list)
transfer.fit(comment_list)
x = transfer.transform(comment_list).toarray()

# 切分训练集和测试集
x_train = x[:10]
y_train = y[:10]
x_test = x[10:]
y_test = y[10:]

# 训练模型
estimator = MultinomialNB()
estimator.fit(x_train, y_train)

y_pred = estimator.predict(x_test)

print(accuracy_score(y_test, y_pred))

聚类算法

无监督学习，根据样本的内在相似性，把数据划分成若干个簇（Cluster）

概念

相似性的度量方法：

  1. 距离度量：欧式距离（最常用）、曼哈顿距离、余弦相似度

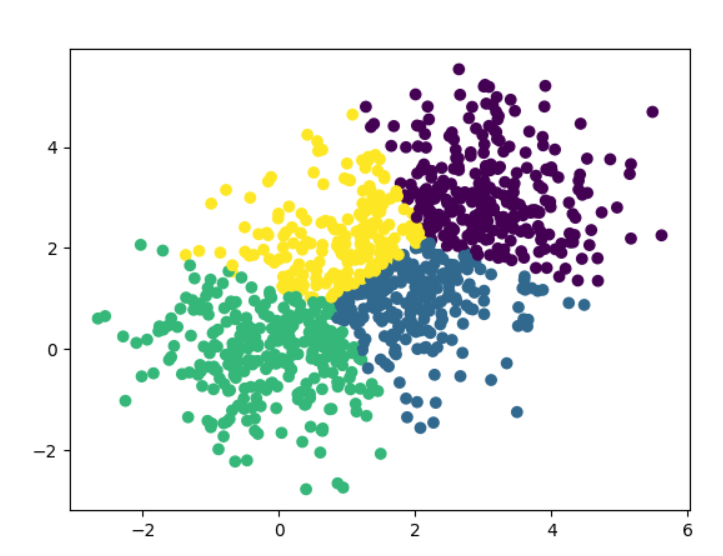
KMeans

是划分式聚类中最经典、最常用的无监督学习算法，核心目标是：给定 k 个簇的数量，将数据集划分为 k 个簇，使得簇内样本的相似度最高，簇间样本的相似度最低

步骤：

  1. 随机选择k个样本点作为聚类中心
  2. 每个样本选择最近的中心聚集成簇
  3. 每个簇算出自己的中心点（不一定是样本点）
  4. 之后用这个新的中心的重新聚类
  5. 重复上面过程，直到生成的中心点和上次一样时停止

评估指标

误差平方和SSE

SSE = 簇内每个点到质心距离的平方和，所有簇之和

值越小越好

轮廓系数法SC

计算一个样本到簇内其他样本的平均距离a

计算一个样本到最近簇内其他样本的平均距离b

轮廓系数 = (b - a) / max(a, b)，范围为[-1, 1]

计算所有样本的平均轮廓系数，值越大聚类效果越好

代码

KMeans实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from sklearn.cluster import KMeans          # 聚类api
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs     # 按照正态分布生成数据集
from sklearn.metrics import calinski_harabasz_score # 评价指标

# 样本数量, 特征数量，标签种类数(聚簇核心点)，标准差，随机种子
x, y = make_blobs(n_samples=1000, n_features=2, centers=[[0, 0], [1, 1], [2, 2], [3, 3]], cluster_std=1.0, random_state=0)

# 簇的数量
estimator = KMeans(n_clusters=4, random_state=0)

estimator.fit(x)
y_pred = estimator.predict(x)

# 评分越高越好
print(calinski_harabasz_score(x, y_pred))

# 绘图
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()

SSE值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.metrics import calinski_harabasz_score


x, y = make_blobs(n_samples=1000, n_features=2, centers=[[0, 0], [2, 2], [4, 4], [6, 6]], random_state=23)

sse_list = []
for k in range(1, 100):
    estimator = KMeans(n_clusters=k, max_iter=100, random_state=23)
    estimator.fit(x)
    sse_list.append(estimator.inertia_)

# 绘制随着簇的数量的增加，SSE值的变化曲线
plt.figure(figsize=(20, 20))
plt.xticks(range(0, 101, 3))
plt.grid()
plt.plot(range(1, 100), sse_list)
plt.show()

学习笔记 > AI
#AI
机器学习
http://xwww12.github.io/2025/11/24/AI/机器学习/
作者
xw
发布于
2025年11月24日
许可协议