python数学

回归

预测

目标函数

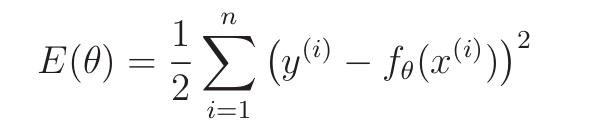
• E是Error的首字母
• i表示第i个训练数据
• y为实际值，f为预测值
• 最优化问题：找到让E最小的θ
• 使用平方而不是绝对值、乘以1/2，是为了后面微分计算方便

最小二乘法

调整θ让E变小

最速下降法/梯度下降法

最速下降法有容易陷入局部最优解的问题

求导，然后往导数符号相反的方向增减

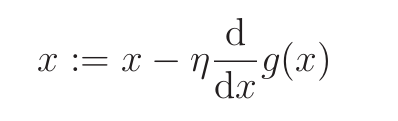
• :=和编程里的=一个意思
• り为学习率，控制值的变化幅度

多项式回归

当曲线方程为：

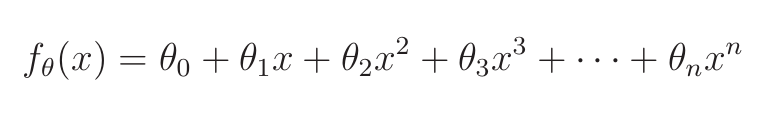
时，每个参数的更新表达式为：

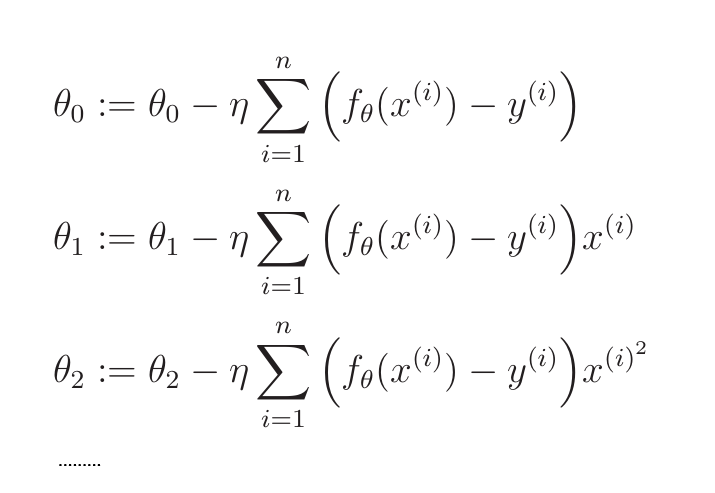
多重回归

包含了多个变量

随机梯度下降法

最速下降法使用了所有训练数据的误差，

而在随机梯度下降法中会随机选择一个或多个训练数据，并使用它来更新参数

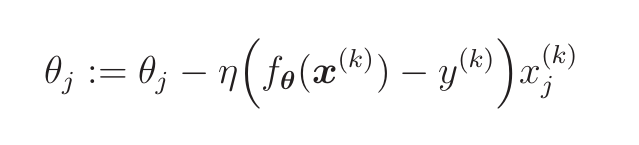
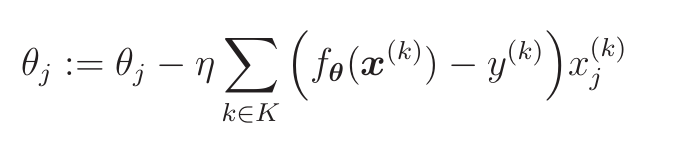
• K为含有m个训练数据的集合

分类

有标签，有监督学习

二分类

将训练数据分类成两类，线性可分。

（假设训练数据是二维的）将训练放在坐标轴上，可通过一条直线将训练数据分成两类

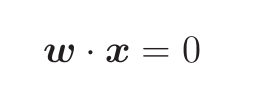
• w意思是权重向量，是要找的直线的法向量
• 通过训练找到权重向量
• 和w夹角在0°~90°和270°~360°为正，90°~270°为负

权重向量的更新表达式

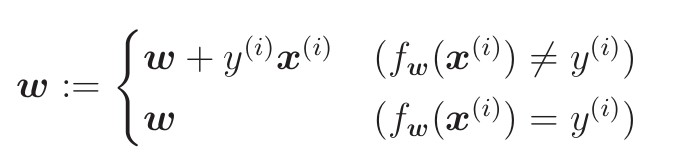
• 预测结果和标签相同时，权重不变
• 预测结果和标签不同时
  • 标签为正则做加法
  • 标签为负则做减法

逻辑回归

sigmoid函数

sigmoid函数用来把数据转化成0~1上的数

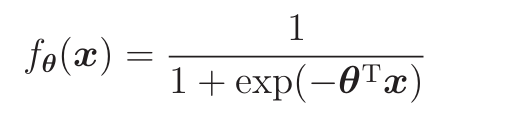
• exp为指数函数，底数为e

• 

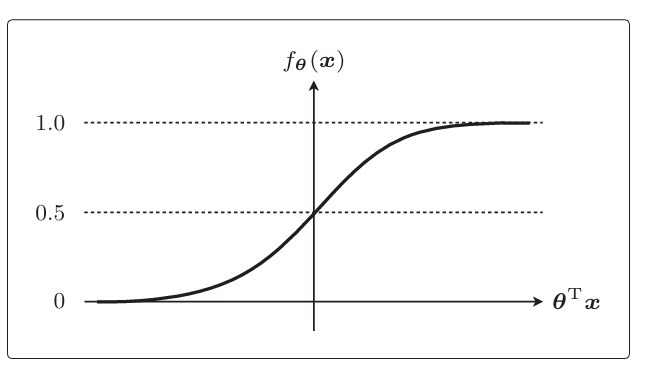
  把f(θ)看做概率，>=0.5时分类为1，<0.5时分类为0

  即θx >= 0时为1，θx < 0时分类为0

  θx = 0称为决策边界

似然函数

是逻辑回归的目标函数

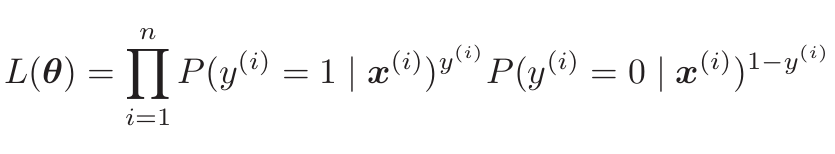
• 目标是找到参数θ，使得L(θ)最大化

• 求导时乘法比较复杂，一般取对数后再计算

  

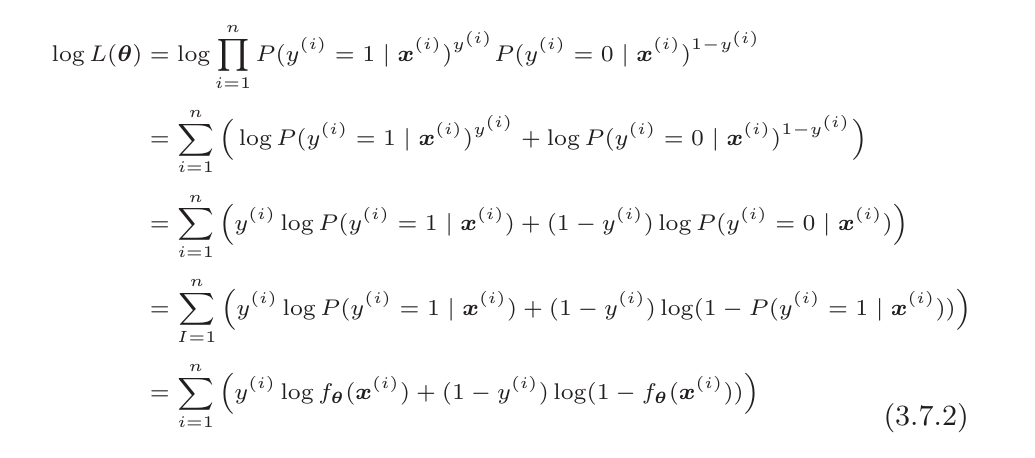
  这个就是逻辑回归的目标函数

对这个目标函数对θ求导得：

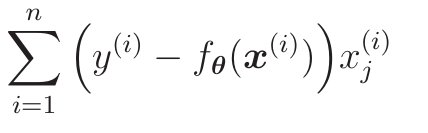
因为要L(θ)越大越好，故参数更新表达式为：

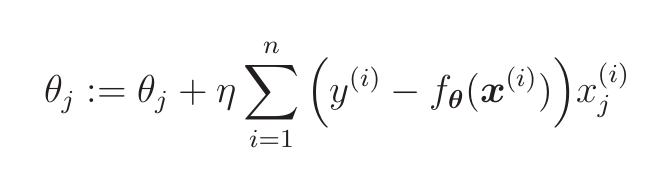
为了和回归时的符号一样，改成：

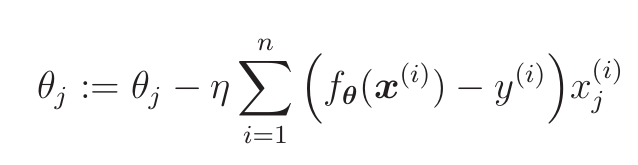
线性不可分

即用直线不能分类的问题

通过加入更高阶的参数让直线变曲线

聚集

无标签，无监督学习

评估模型的方法

交叉验证

交叉验证为，将数据分为测试数据和训练数据

• 回归：计算测试数据的方差
• 分类：分类正确的占比
  • 精确率：被分类到一边的正确个数占比
  • 召回率：某一种被分类正确的占比
  • F值、F1（F measure）：2/( 1/精确率 + 1/召回率 )，只要有一个低了就会拉低F值，是精确率和召回率的调和平均值

K折交叉验证：数据分成K分，重复K次交叉验证，每次拿不同的一份数据作为测试数据

正则化

避免过拟合的方法

1. 增加训练数据
2. 使用简单的模型
3. 正则化