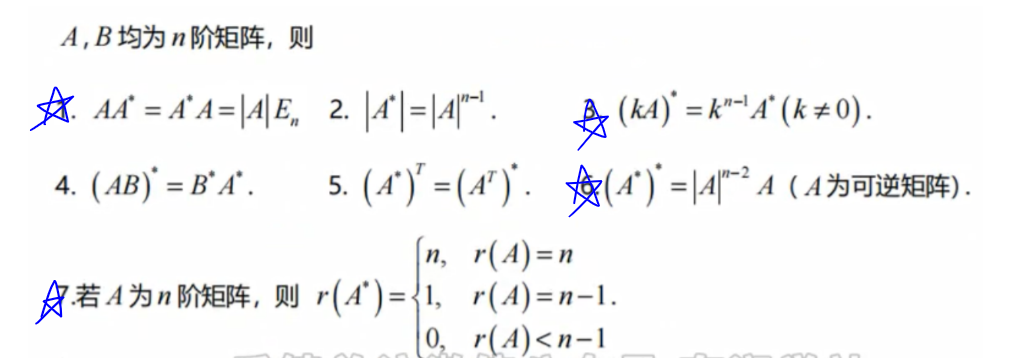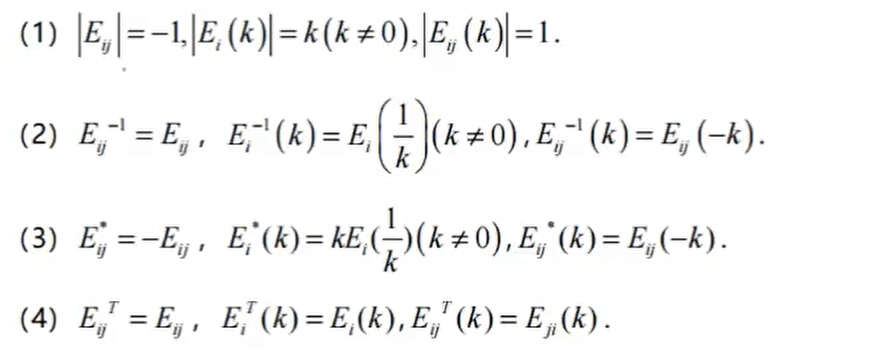线代强化

行列式的定义、性质与计算

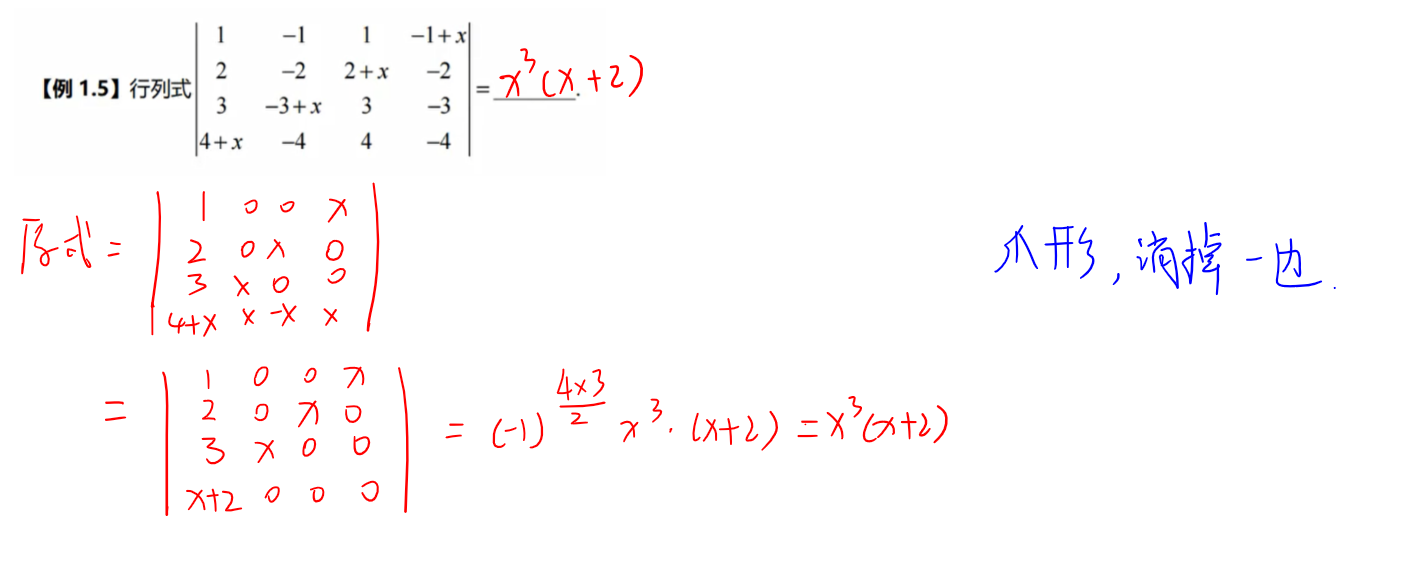
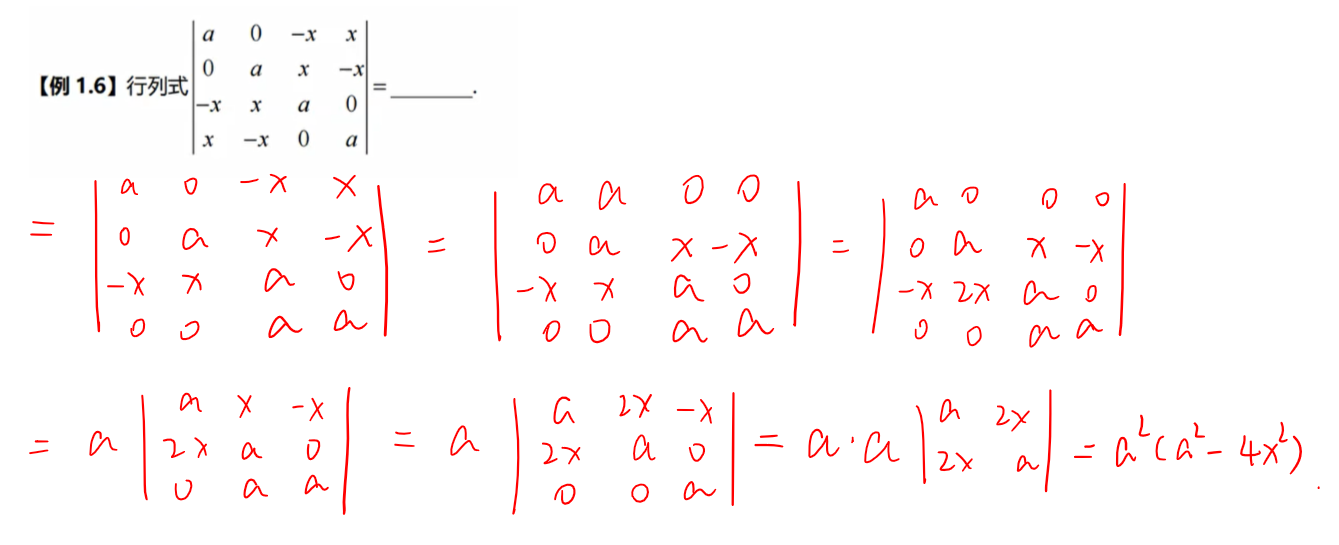
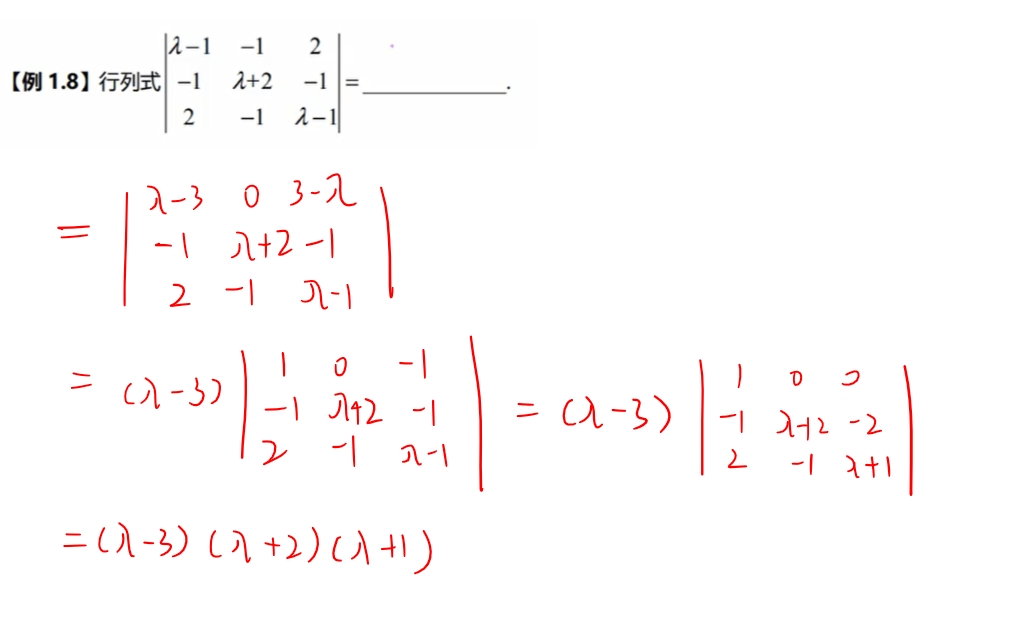
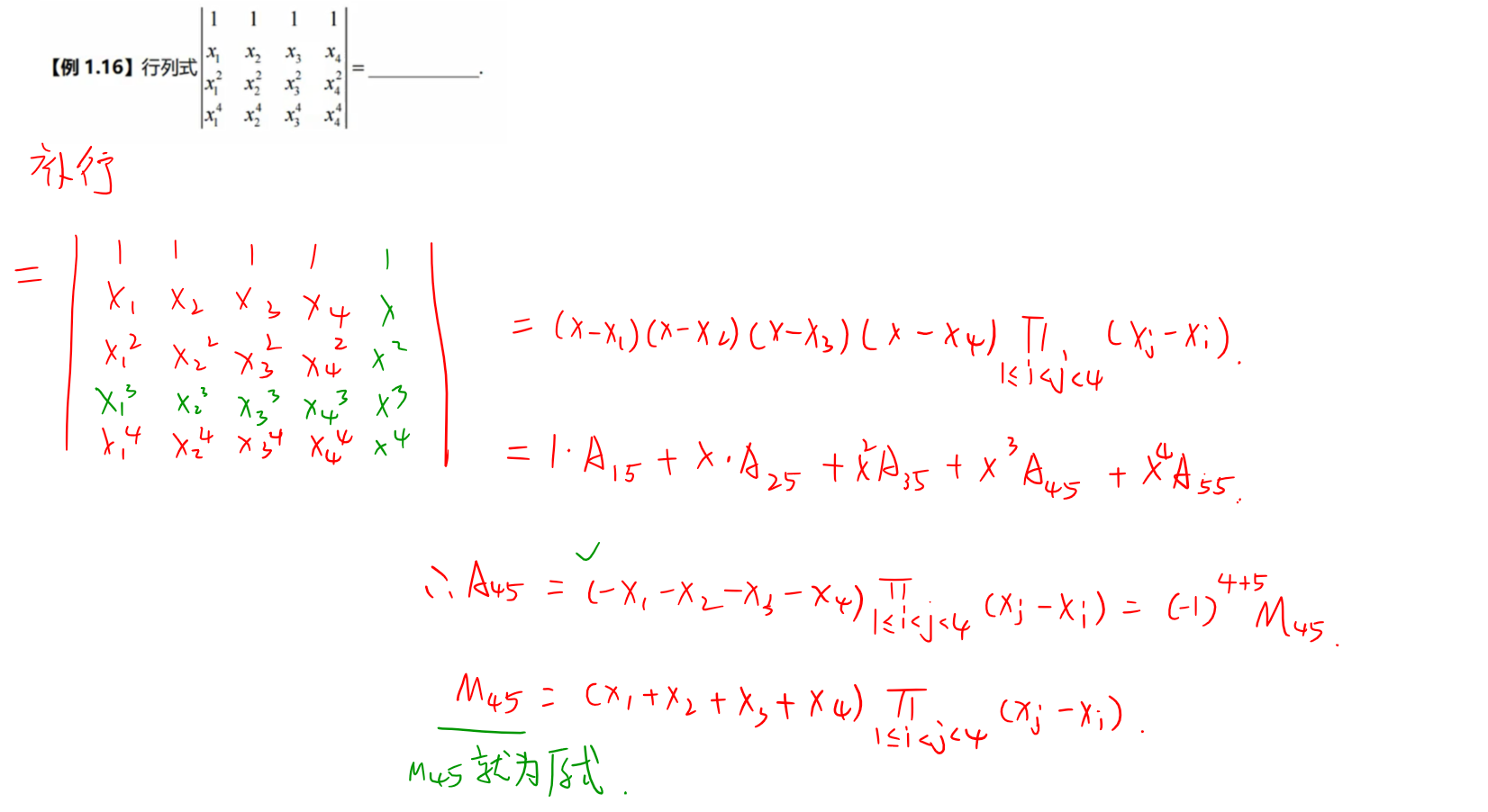
抽象行列式、矩阵运算

分块行列式

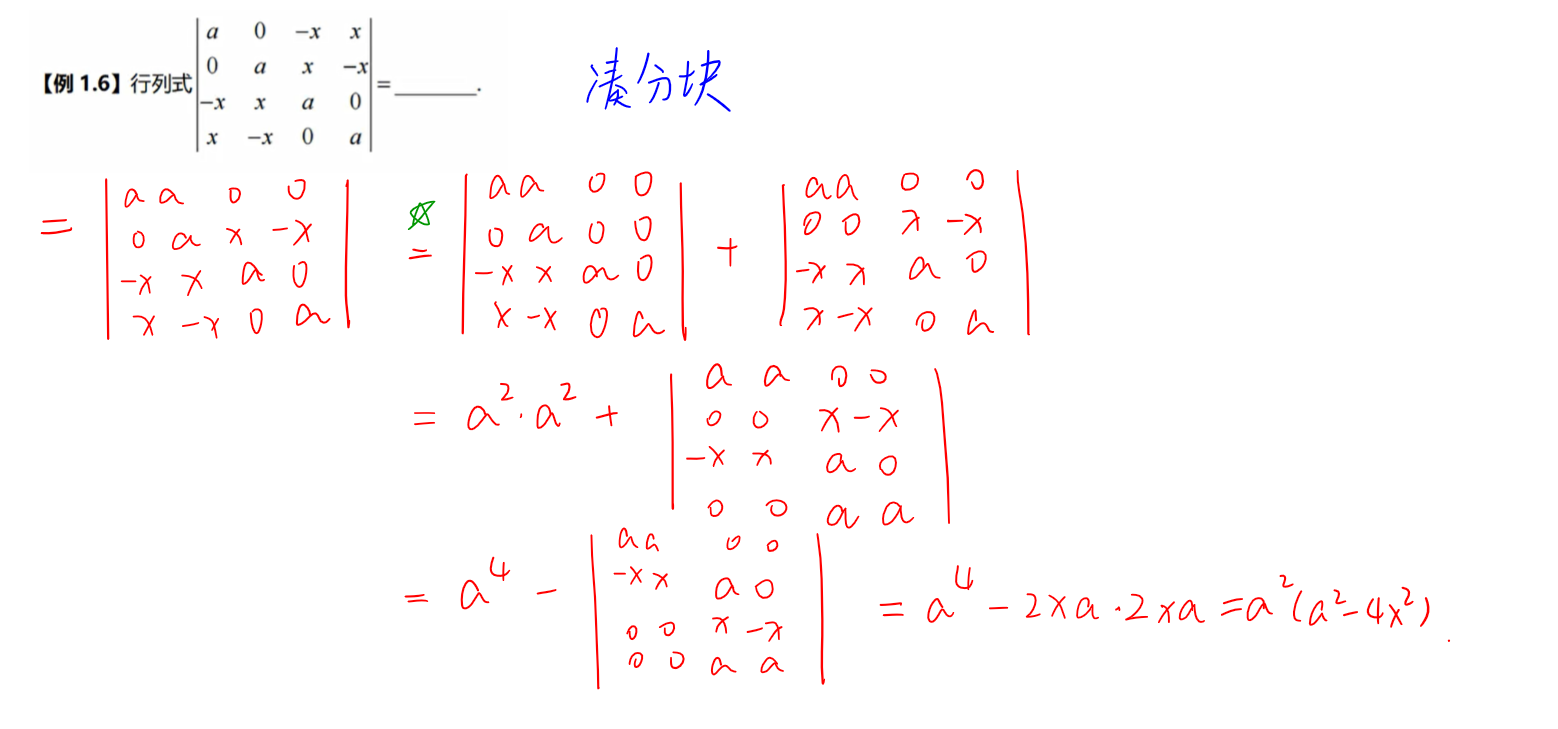
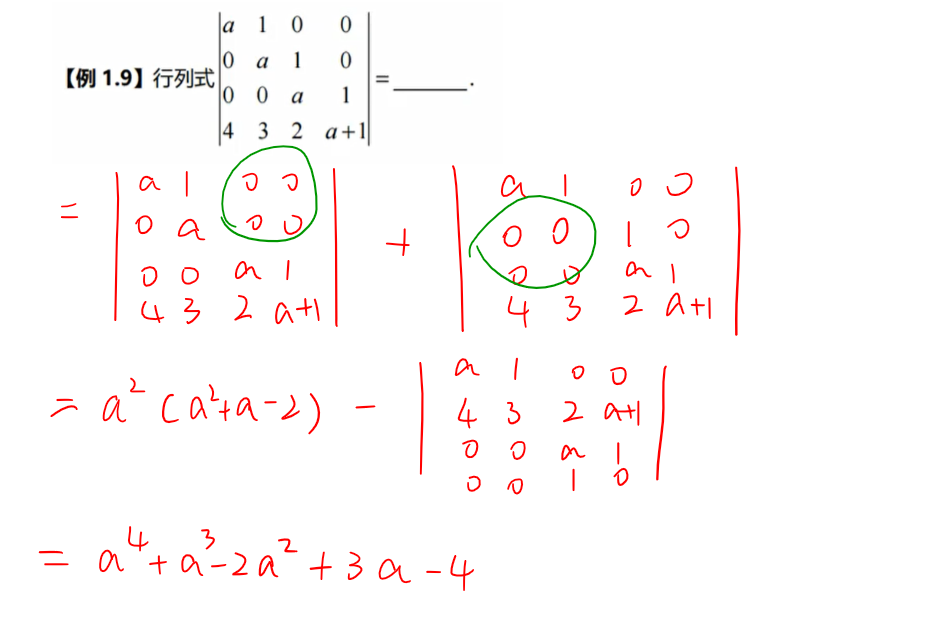
抽象行列式运算

行列式性质

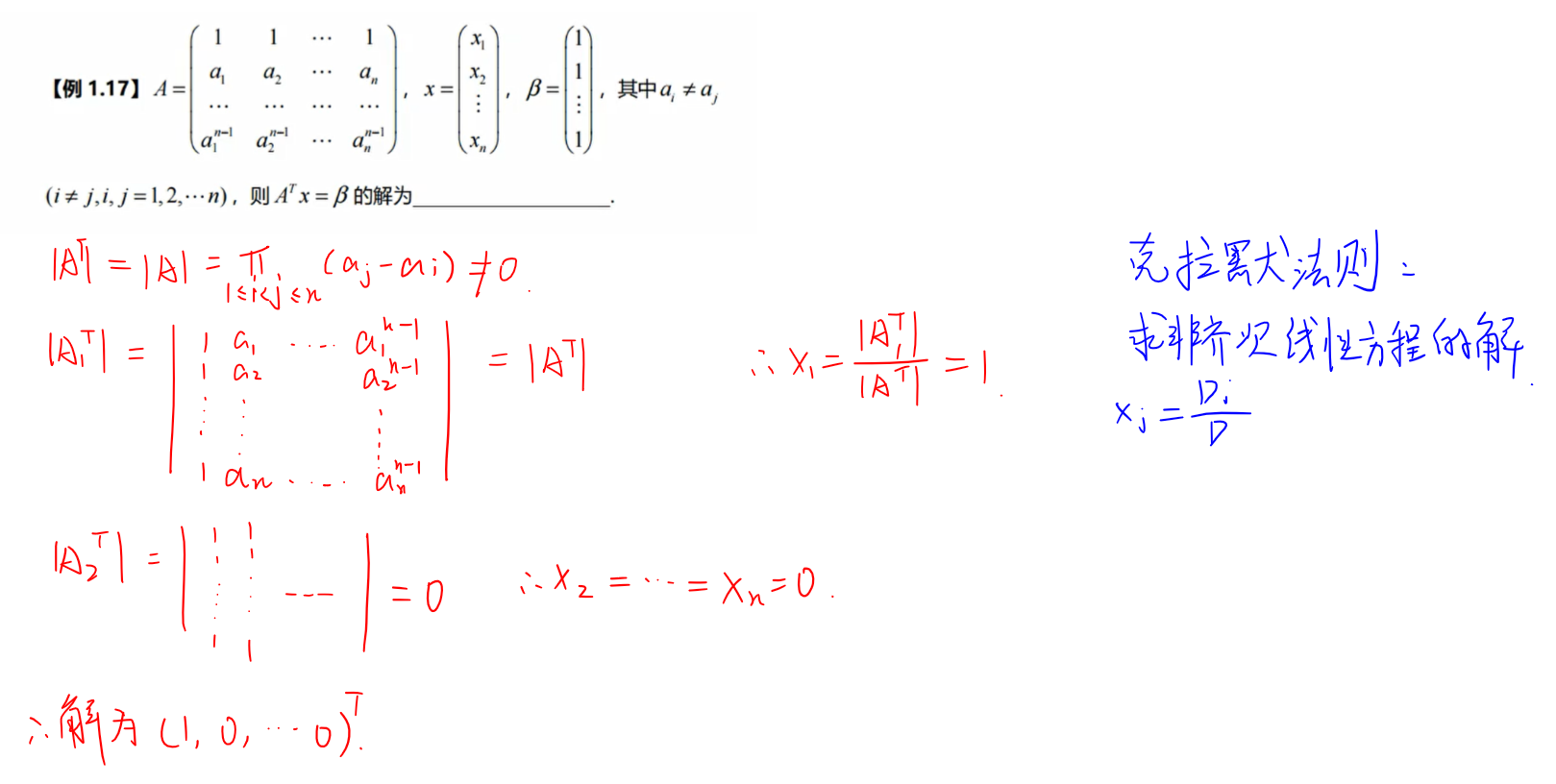
矩阵的基本运算

方阵的幂✨

三种方法：

1. 找规律
2. 成比例
3. 可对角化

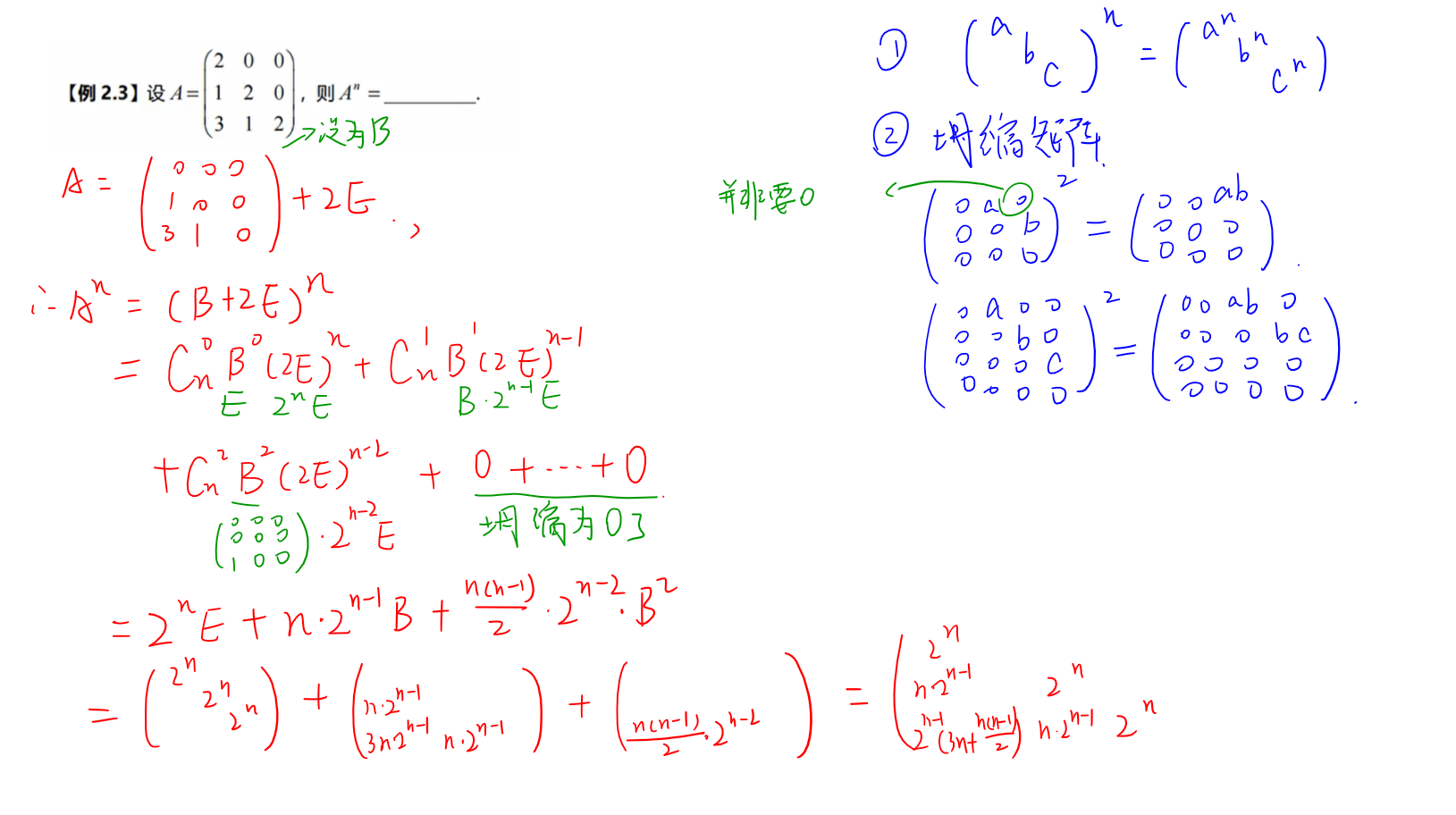
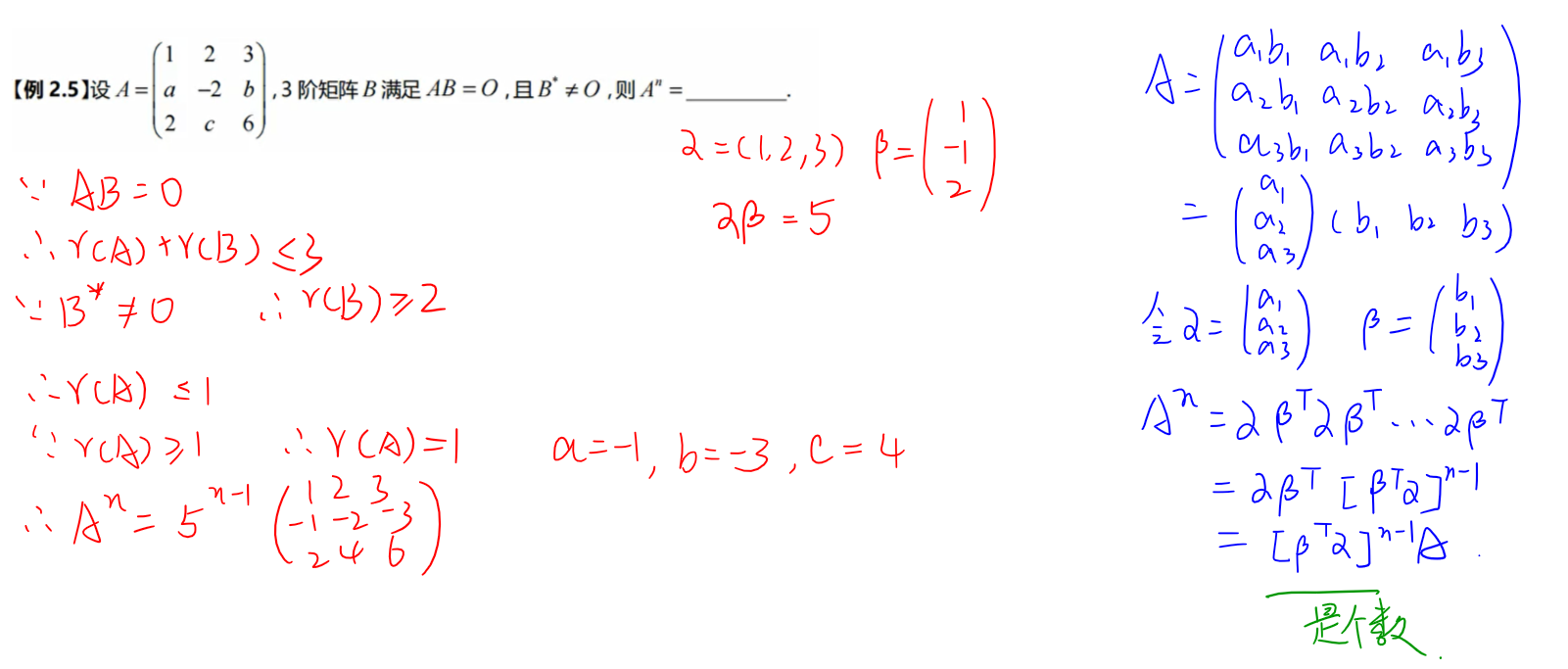
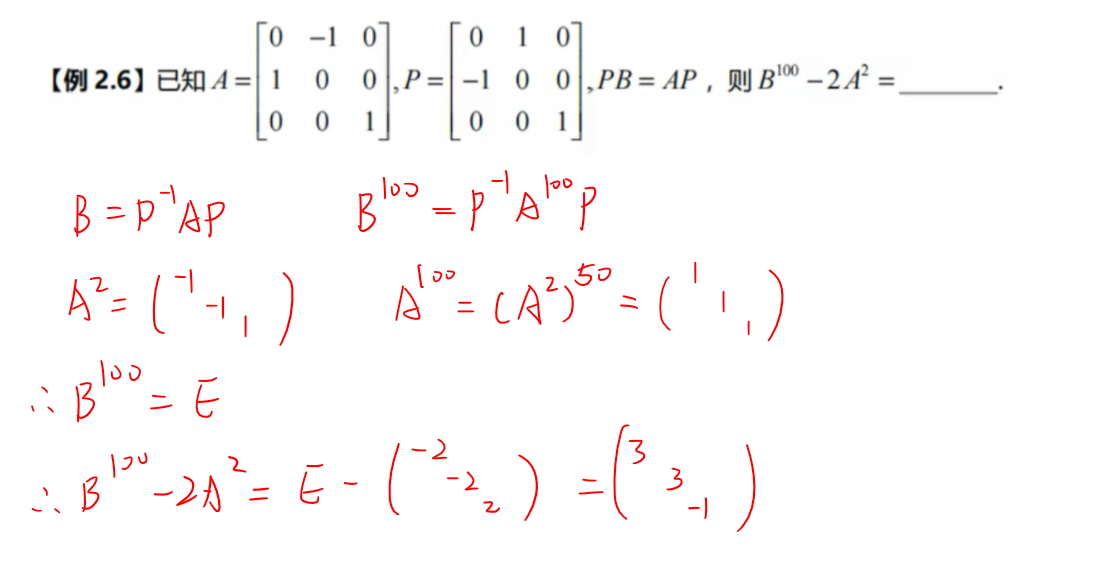
伴随矩阵✨

总结

逆、初等矩阵、秩

矩阵的逆

初等矩阵

初等矩阵定义：单位矩阵作一次初等变换所得的矩阵

初等矩阵的性质

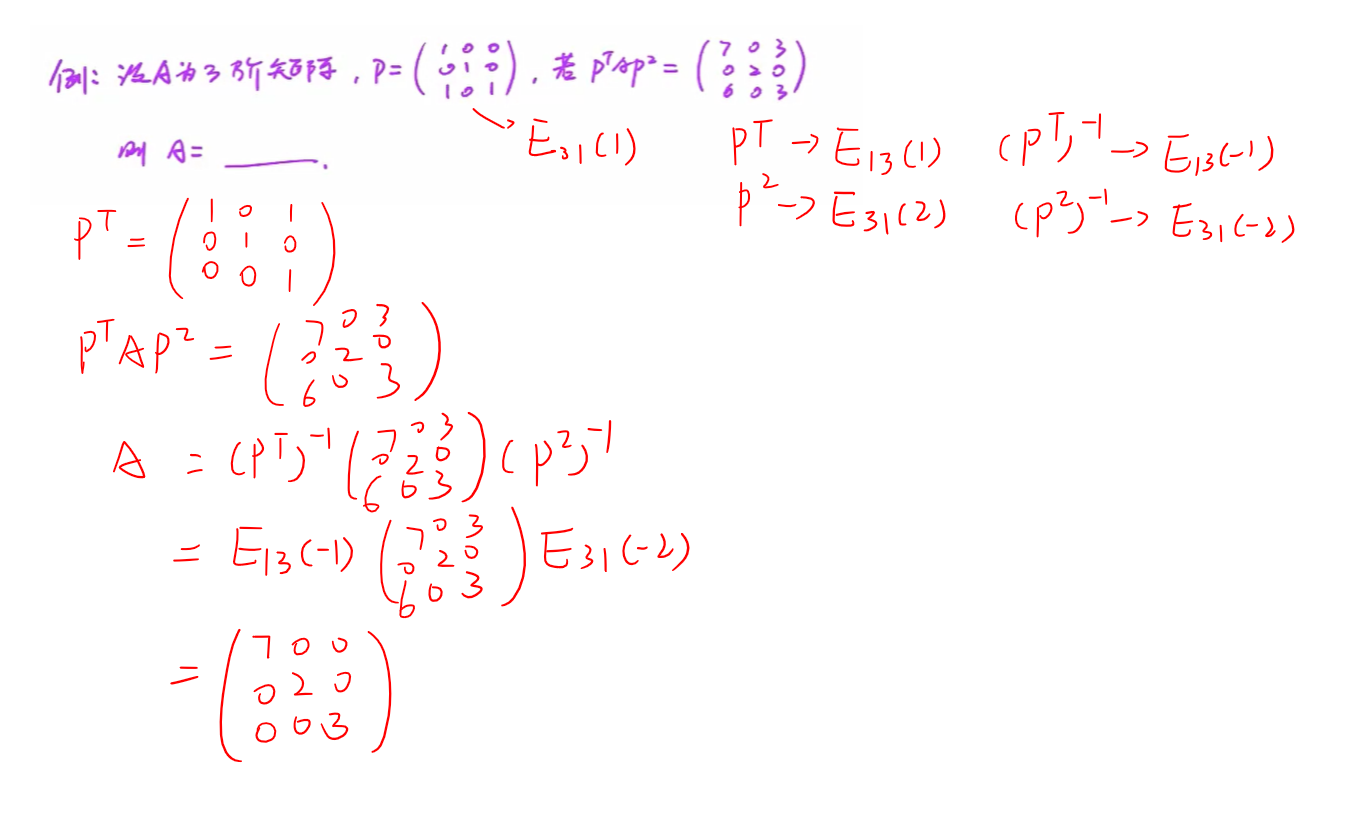
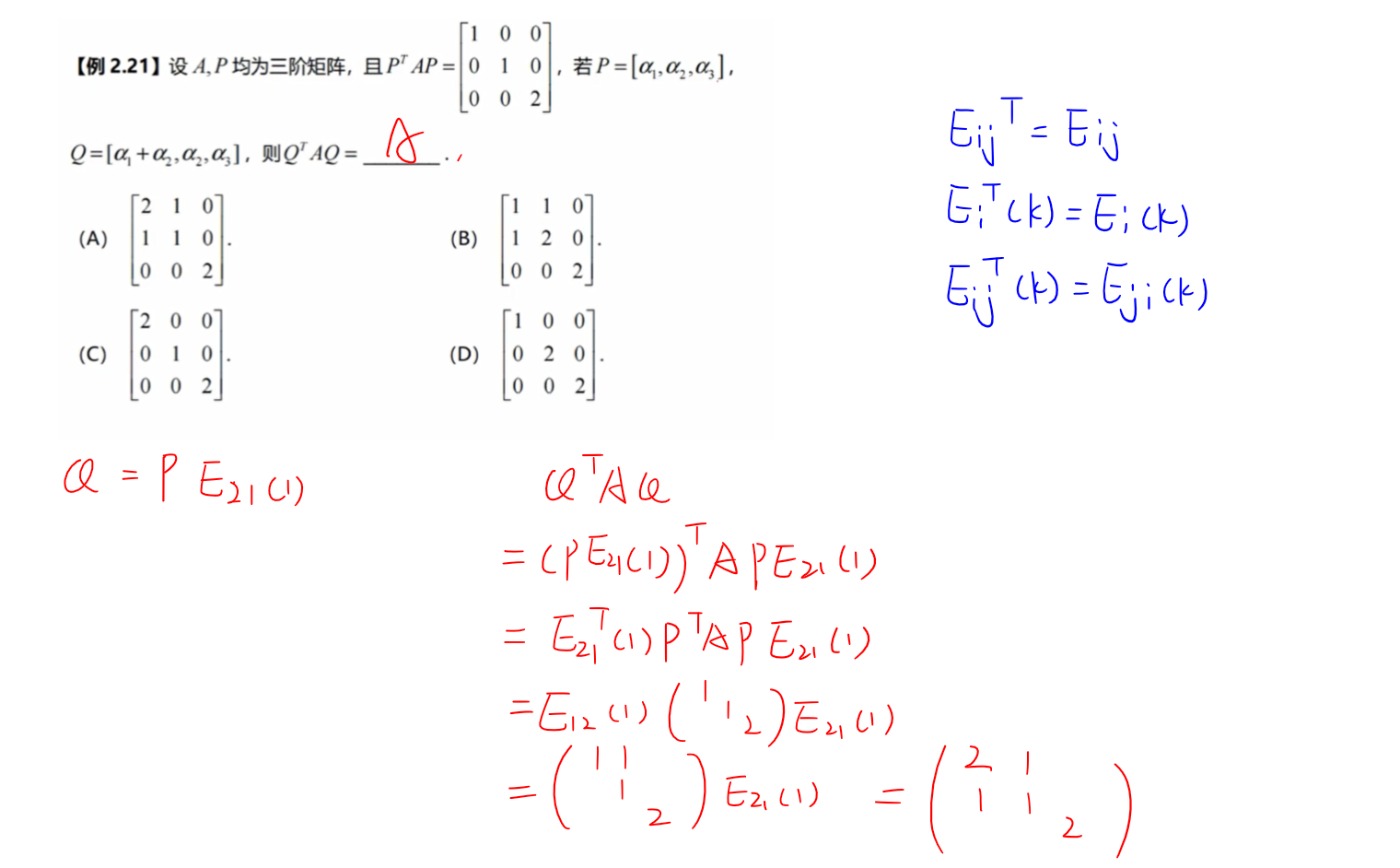
可逆矩阵方程

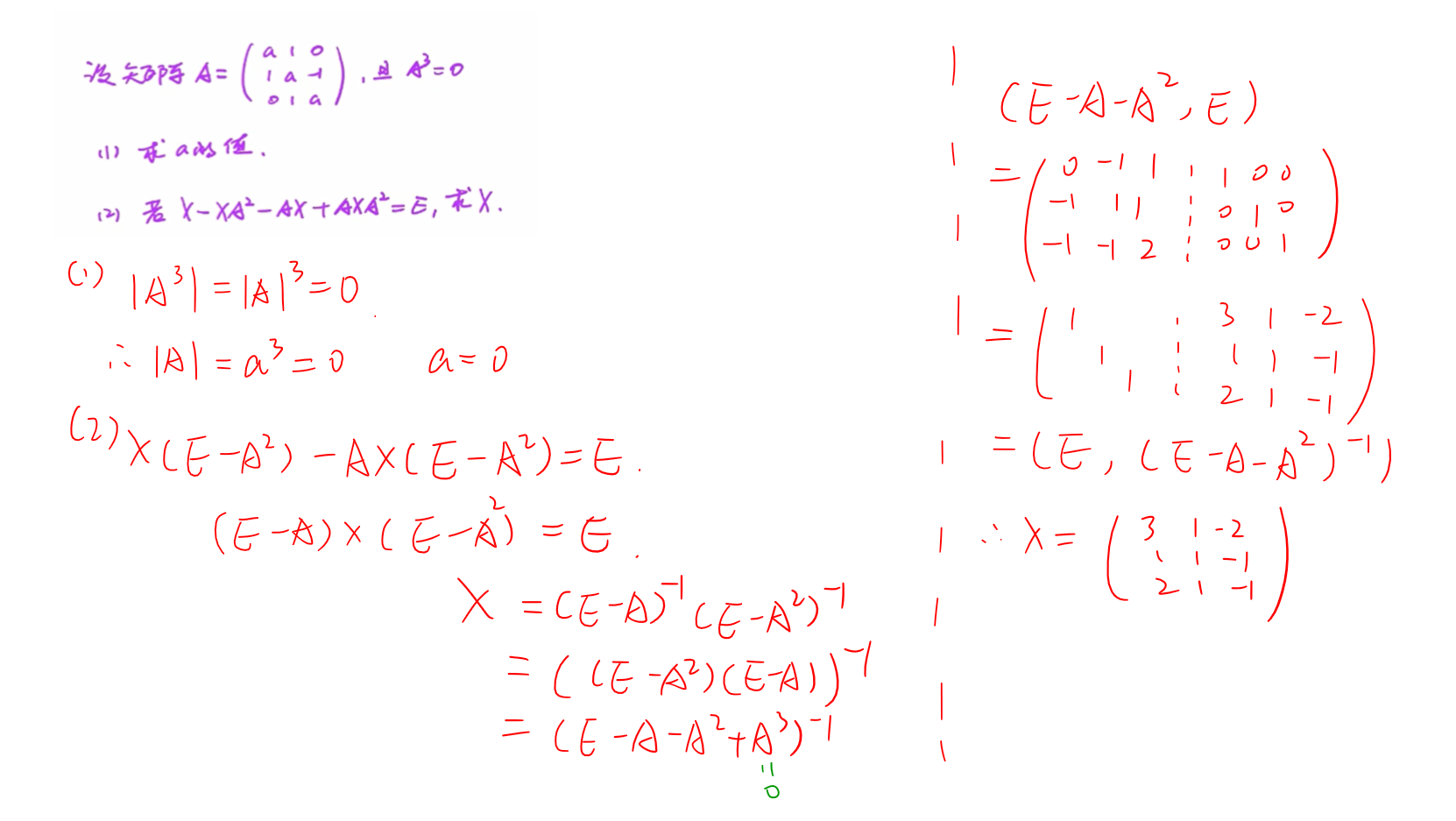
矩阵的秩✨

秩的性质

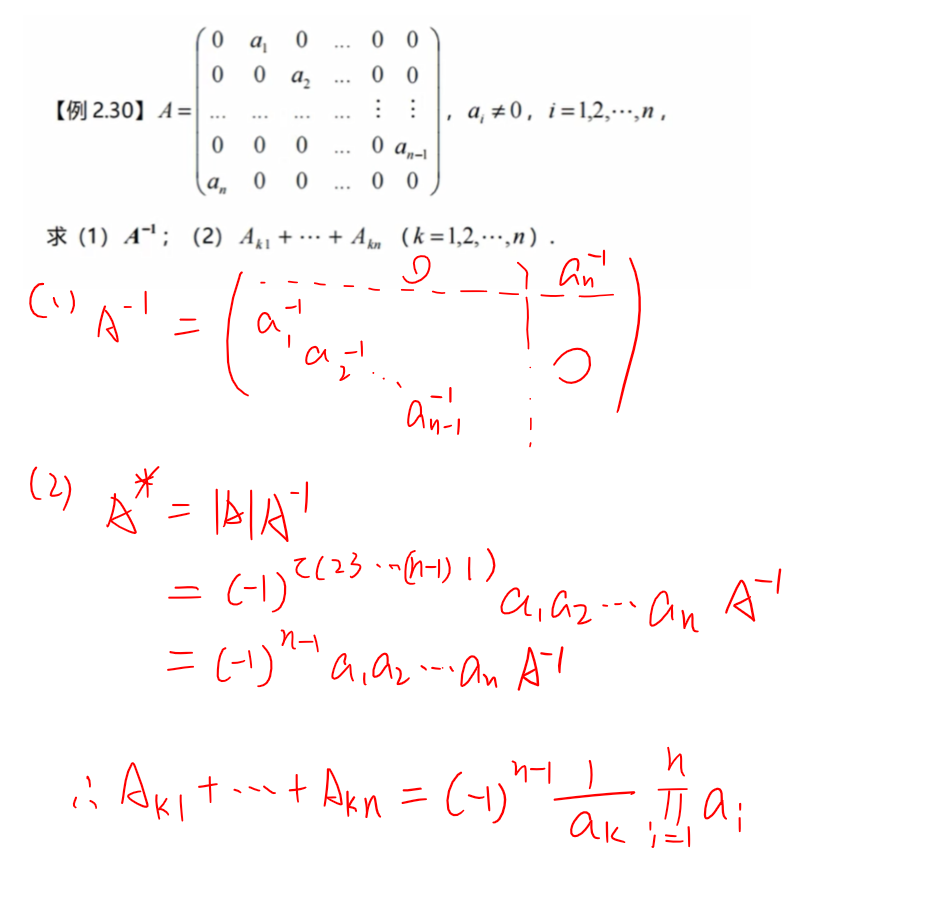
向量组的线性相关性

向量组的线性相关性

求法：

1. 先看秩
2. 不行在用定义

向量组的线性表示

向量组等价

向量组的极大无关组和秩

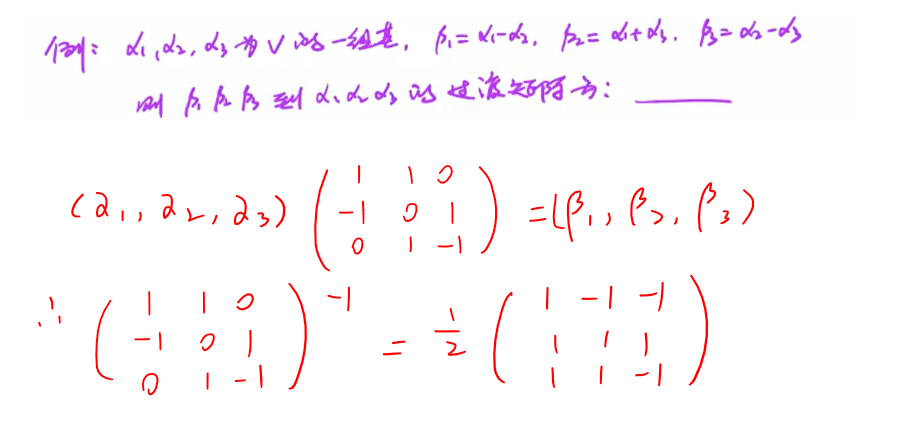
线性方程组

抽象方程组

不可逆矩阵求解

解的结构

公共解

证明方程组A、B同解：

1. 方法1：将A的通解带入B，系数取任何值都成立，此时表示A的解都包含在B中，再证系数矩阵秩相同，则表示AB同解
2. 方法2：证明两个方程组矩阵的行向量组等价，即两个方程组可以互相线性表示

特征值、特征向量与相似矩阵

求特征值：解| λE - A | = 0，得所有的特征值λ

求特征向量：解( λE - A )X = 0，求出基础解系α1, α2, …,则k1α1 + k2α2 + … 为特征向量（k不全为0）

特征值性质：

1. 特征值之和 = 矩阵对角线之和 = 迹
2. 特征值之积 = 矩阵的行列式

特征向量性质：

1. 不同特征值的特征向量是线性无关的
2. m重特征值对应的特征向量 <= m

相似矩阵

相似矩阵

若A ~ B，则秩、迹、行列式相等

相似对角化

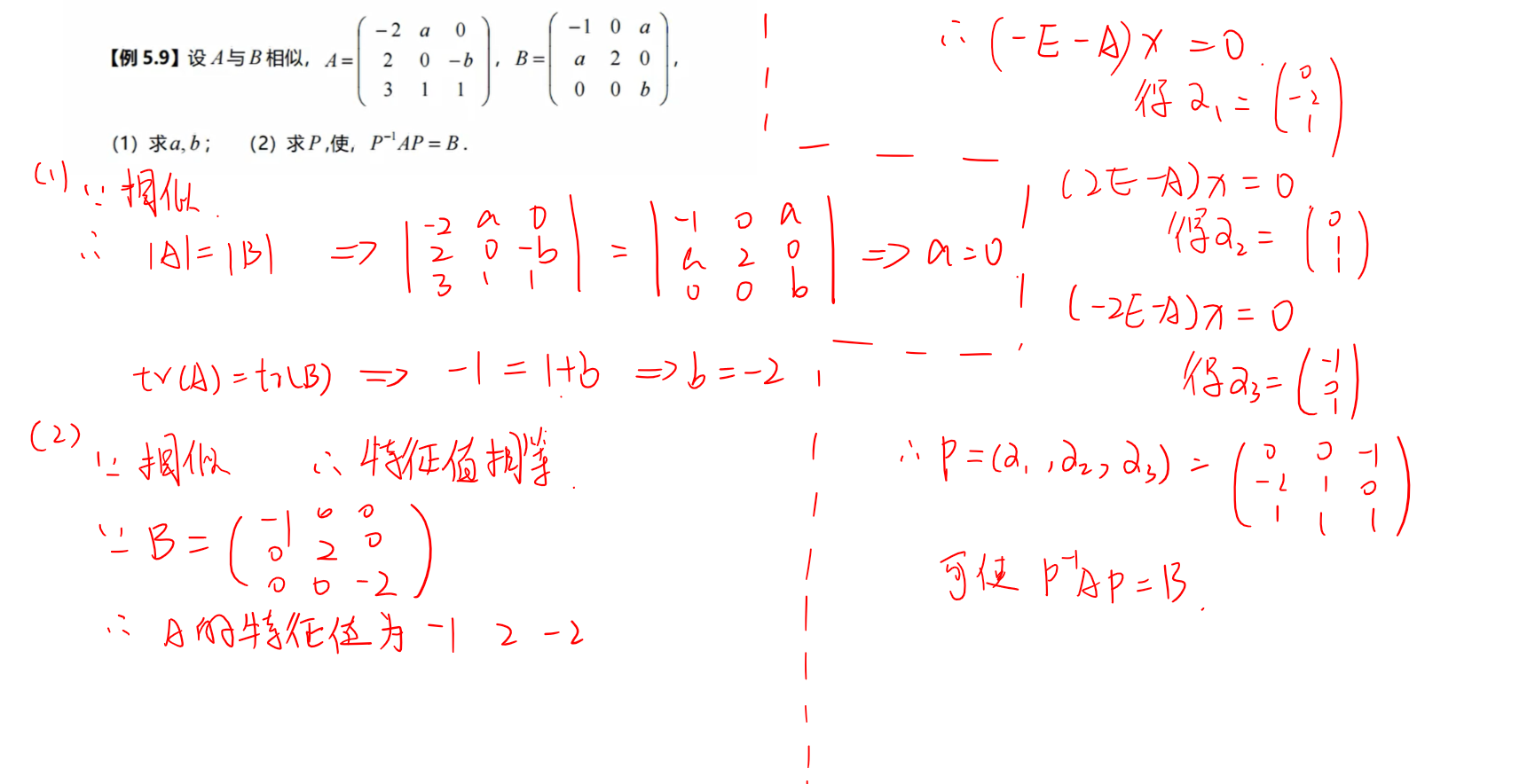
对角化

实对称矩阵

实对称矩阵性质：

1. 不同特征值的特征向量是相互正交的
2. 实对称矩阵必可相似对角化，存在正交矩阵Q，Q^T A Q = diag(λ1，λ2，…，λn)

二次型

二次型化为标准型方法：

1. 用正交变换化为二次型为标准型

   

2. 配方法化为二次型

   

二次型f(x1, x2, x3) = 1 表示的二次曲面

正定二次型

判别正定二次型：

1. 充要条件

   1. 定义：对任意X ≠ 0，X^T A X > 0
   2. A的特征值都大于0
   3. 正惯性指数为n
   4. 顺序主子式全大于0，（负定的奇数阶顺序主子式小于0，偶数阶大于0）

2. 必要条件

   若正定，则|A| > 0，主对角元素都大于0

两个矩阵的关系