数据结构

图

最小生成树

定义：带权连通无向图，权值之和最小的那棵生成树

性质：

1. 若存在权值相同的边，最小生成树可能不唯一
2. 各边权值互不相等，生成树唯一
3. 若无向连通图边数比顶点数少1，则最小生成树为自身

最小生成树算法：

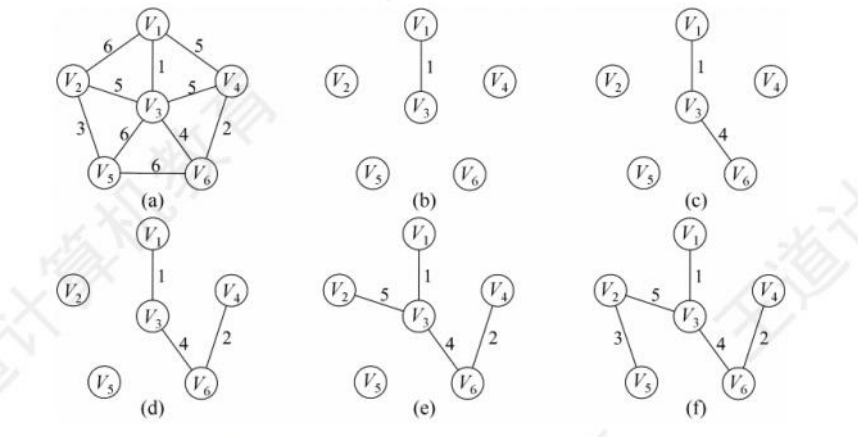
Prim（普里姆）算法

步骤：

1. 贪心，初始时从图中任取一点加入T

2. 之后选择与T最近的顶点加入T，直到选完所有点

时间复杂度O(|V|²)，与边数无关，适合边稠密图

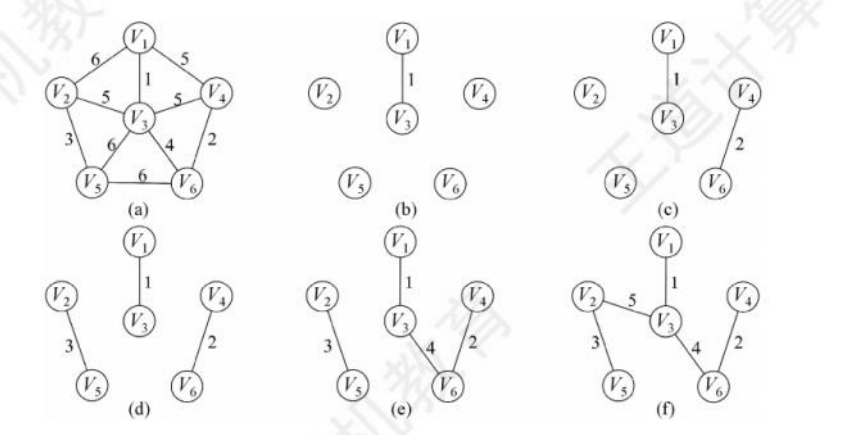
Kruskal（克鲁斯卡尔）算法

步骤：

1. 贪心，权值由小到大选择
2. 若该边依附的点在T中不同的连通分量，则将边加入T，直至所有点都在一个连通分量上

时间复杂度O( |E|log2(|E|) )，适合边稀疏而顶点较多的图

最短路径

定义：

1. 带权路径长度：从一个顶点到另一个顶点路径上边的权值之和
2. 最短路径：权值之和最短的路径

最短路径算法：

Dijkstra（迪杰斯特拉）算法

求单源最短路径

贪心，边不能为负数

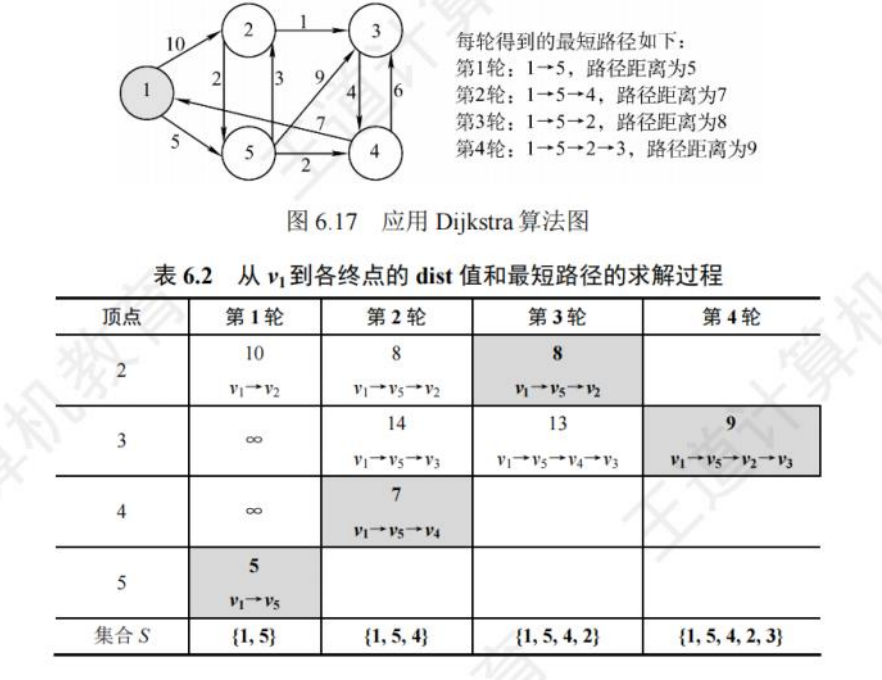
时间复杂度O(|V|²)

Floyd（弗洛伊德）算法

求每对顶点间的最短距离

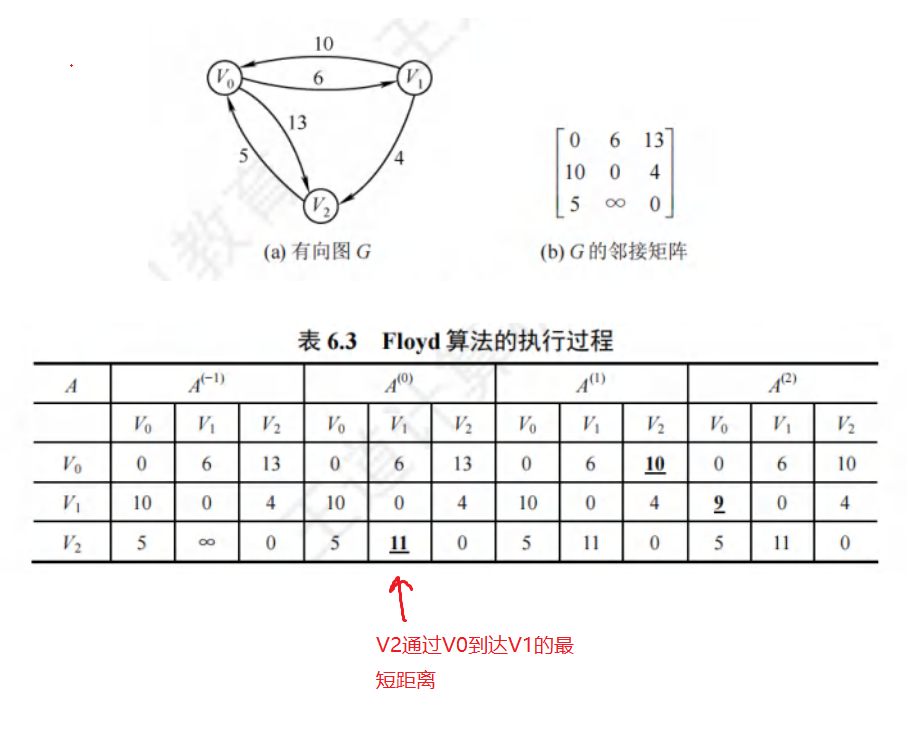
时间复杂度O(|V|³)

拓扑排序

概念：

1. AOV网：顶点表示活动的网络
2. DAG图：有向无环图
3. AOE网：边表示活动的网络，点表示事件

关键路径

定义：

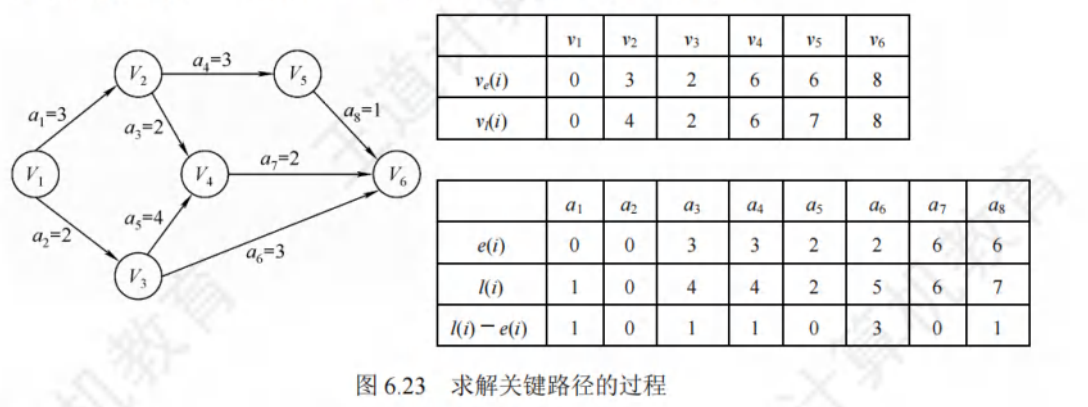
关键路径：AOE网中，具有最大路径长度的路径

关键活动：关键路径上的活动

最早发生时间ve(k)：从源点到顶点vk的最长路径长度，决定了从vk开始的活动的最早开工时间

最迟发生时间vl(k)：在不推迟整个工程完成的前提下，事件必须开始的最迟时间

查找

二叉查找树

平衡二叉树

1. 构造深度为h的平衡二叉树的最少节点数

   n0 = 0, n1 = 1, nh = 1 + n(h-1) + n(h-2)

2. 顺序插入时，平衡二叉树的高度

   如果结点个数为2^k - 1则为满二叉树

B-树

度为m的B-数性质

1. 每个非根节点最多可以有 m 个孩子，最少有 m/2(向上取整) 个孩子
2. 每个非根节点最多可以有 m-1 个key，最少有 m/2(向上取整) - 1个key
3. 根节点不是终端节点，则根节点至少 1 个key，至少有两个孩子
4. 所有的叶子节点都在同一层，表示查找失败节点

例题

1. 节点数的上下限

哈希表

注意点

1. 平均查找长度与装填因子α直接相关，不直接依赖于表长或表中已有元素
2. 聚集是因为选择了处理不当的处理冲突方式

例题

面试简答

1.稀疏的无向图用什么存储最好

使用邻接表存储最好，仅需 O(n+2e) 空间（n 为节点数，e为边数）；

而邻接矩阵需要O(n^2)的空间

2.空串和空格串是否一样？

不一样。空串是一个长度为 0 的字符串，不包含任何字符；

空格串是一个由空格字符组成的字符串，长度至少为 1。

3.怎么判断一个图是否有环？解释拓扑排序的过程

常用的方法有 深度优先搜索（DFS） 和 拓扑排序

在 DFS 遍历过程中，如果遇到一个已经被访问过且仍在递归栈中的节点，则说明图中存在环。

拓扑排序仅适用于有向无环图（DAG）。如果图中存在环，则无法完成拓扑排序。

拓扑排序步骤：

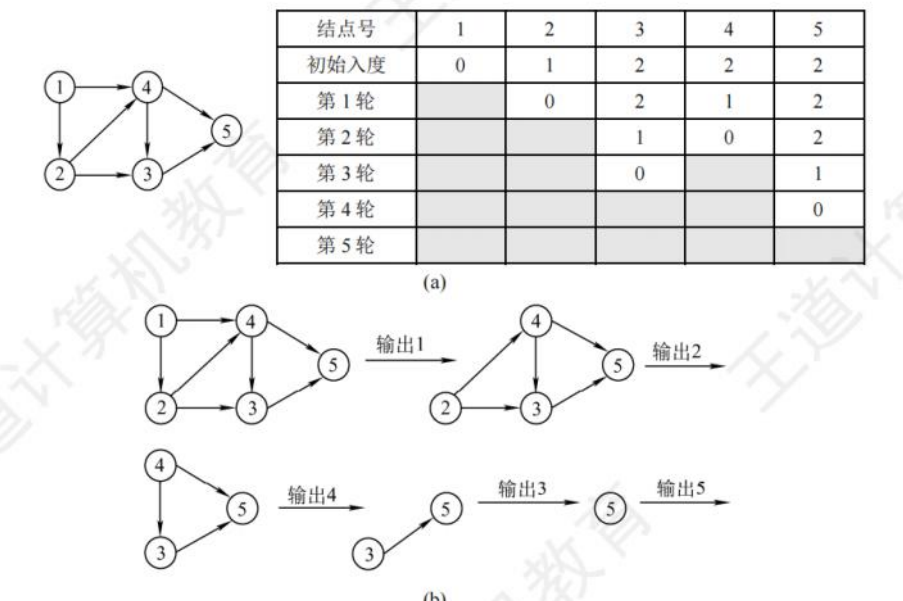
1. 计算每个节点的入度（即有多少条边指向该节点）。
2. 将所有入度为 0 的节点加入队列。
3. 从队列中取出一个节点，将其加入拓扑排序结果中，并减少其所有邻居的入度。
4. 如果某个邻居的入度变为 0，则将其加入队列。
5. 重复上述过程，直到队列为空。
6. 如果拓扑排序结果中的节点数小于总节点数，则说明图中存在环。

4.循环队列怎么判断队列满/空

当队头指针和队尾指针指向同一位置时，说明队列中没有元素；

判断队列满有两种办法：

1. 牺牲一个存储空间，队尾指针的下一个位置是队头指针时，说明队列已满。
2. 维护一个变量 size 记录队列中的元素数量，当 size 等于 capacity时，说明队列已满；

5.什么是稀疏矩阵

稀疏矩阵是指矩阵中非零元素的数量远少于零元素的数量

我们可以存储非零元素的行索引、列索引和值来压缩存储稀疏矩阵

6.强连通图，N个顶点最多和最少有多少个边

强连通图是指在有向图中，任意两个顶点之间都存在双向路径

假设顶点数为n，边数最少的情况是图形成一个有向环，边数内n

边数最多的情况是图是一个完全有向图，即图中任意两个顶点之间都有双向边，此时边数为n*(n-1)

7.如何存储二叉树

通常有两种主要方法：顺序存储和链式存储

顺序存储通过数组来表示二叉树，适用于完全二叉树或满二叉树。对于一般的二叉树，顺序存储会浪费空间

链式存储通过节点和指针来表示二叉树，每个节点包含数据域和指向左右子节点的指针

8.什么是广义表

广义表的元素可以是原子或子表，可以表示线性表、树、图等复杂数据结构

9.什么是AOE网，什么是AOV网

AOE 网AOE 网是一种边表示活动、顶点表示事件的有向无环图，描述活动的时间安排和关键路径

AOV 网是一种顶点表示活动、边表示活动之间的先后关系的有向无环图，描述活动之间的先后关系

10.树的基本定义

树（Tree）是计算机科学中一种非常重要的非线性数据结构，它由节点（Node）和边（Edge）组成的层次化、无环的连通数据结构

11.顺序表有什么特点

顺序表使用连续的内存空间存储数据元素

数据元素在内存中按顺序排列，逻辑顺序与物理顺序一致。

特点：支持随机访问，存储密度高，插入或删除元素效率低

12.什么是数据元素

是数据结构中的基本单位，也称为元素或节点，它是数据结构中存储和处理的最小逻辑单元

13.顺序表和链表的异同

相同：都是线性数据结构，都适用于需要存储和处理线性数据的场景

不同：

特性	顺序表	链表
存储方式	连续内存空间	非连续内存空间，通过指针链接
访问方式	随机访问，O(1)	顺序访问，O(n)
插入删除	平均 O(n)	O(1)（已知位置）
空间效率	存储密度高，可能内存浪费	存储密度低，动态分配内存
扩容方式	固定容量，扩容成本高	动态扩容，扩容成本低