解微分方程总结

可分离变量

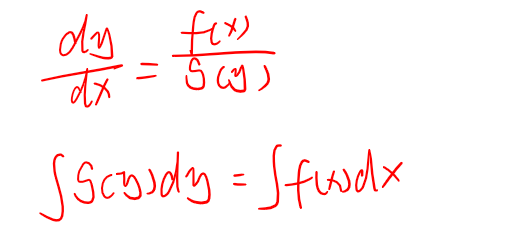
齐次方程

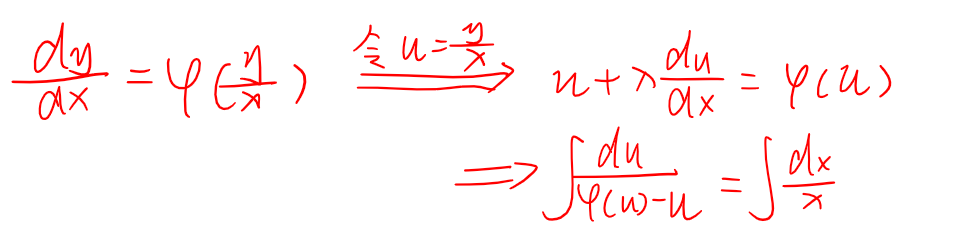
一阶线性方程

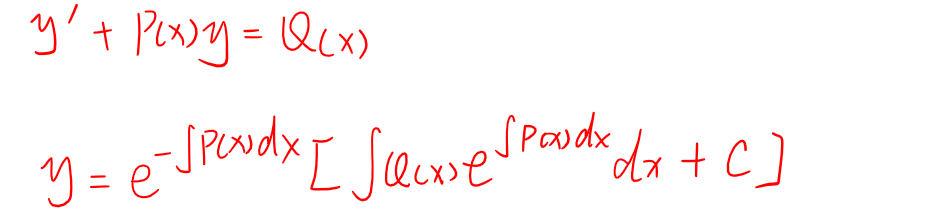
伯努利方程

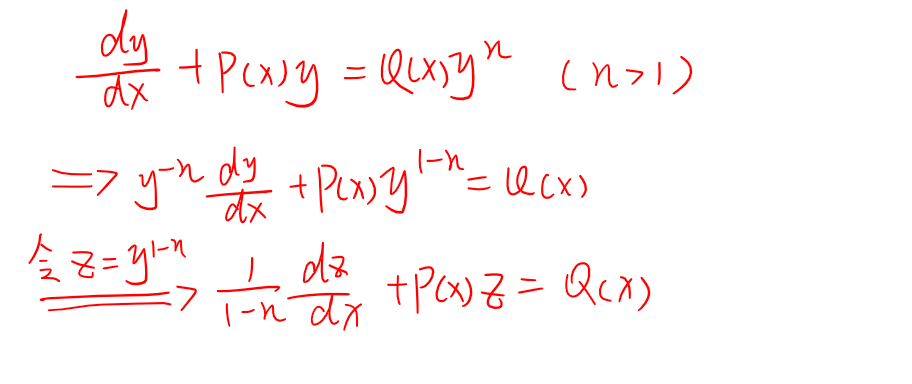
高阶常系数齐次线性方程

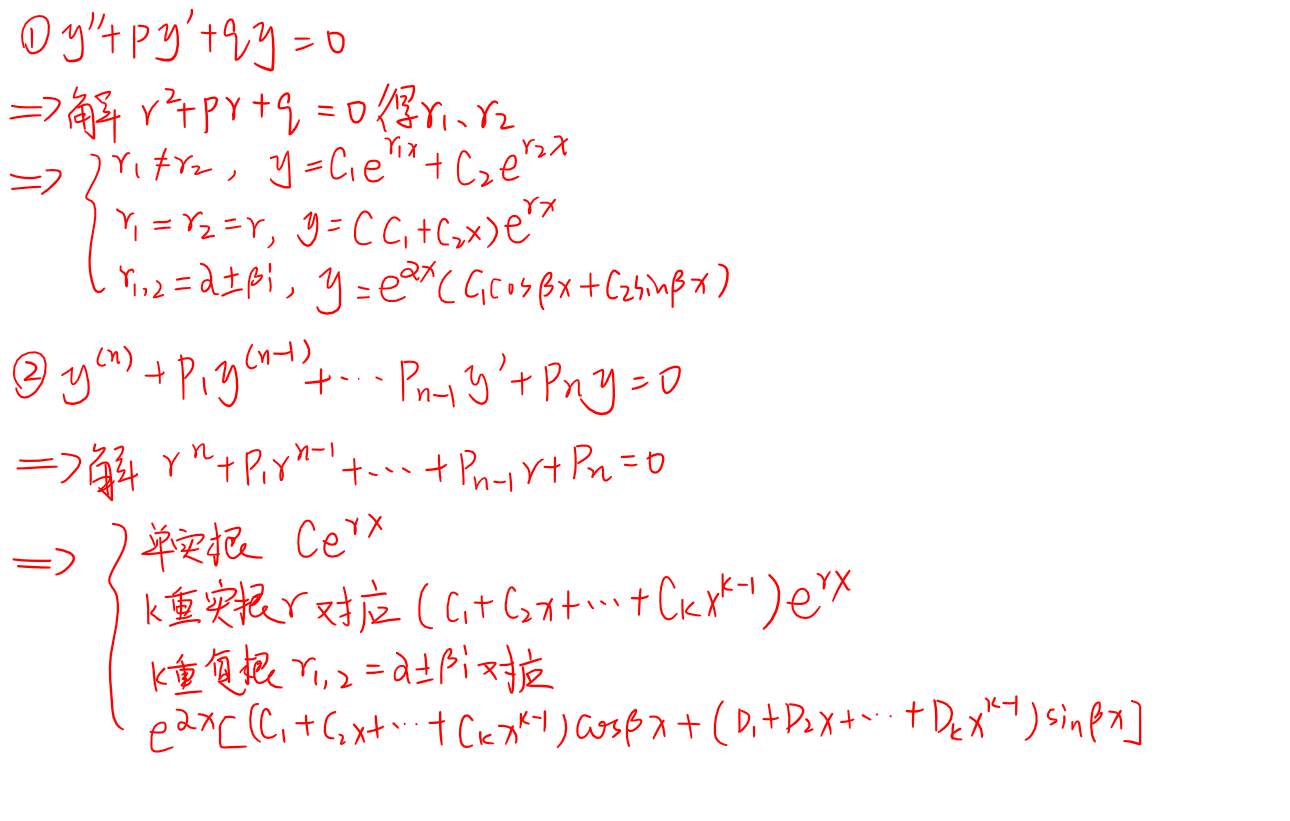
二阶常系数非齐次线性方程

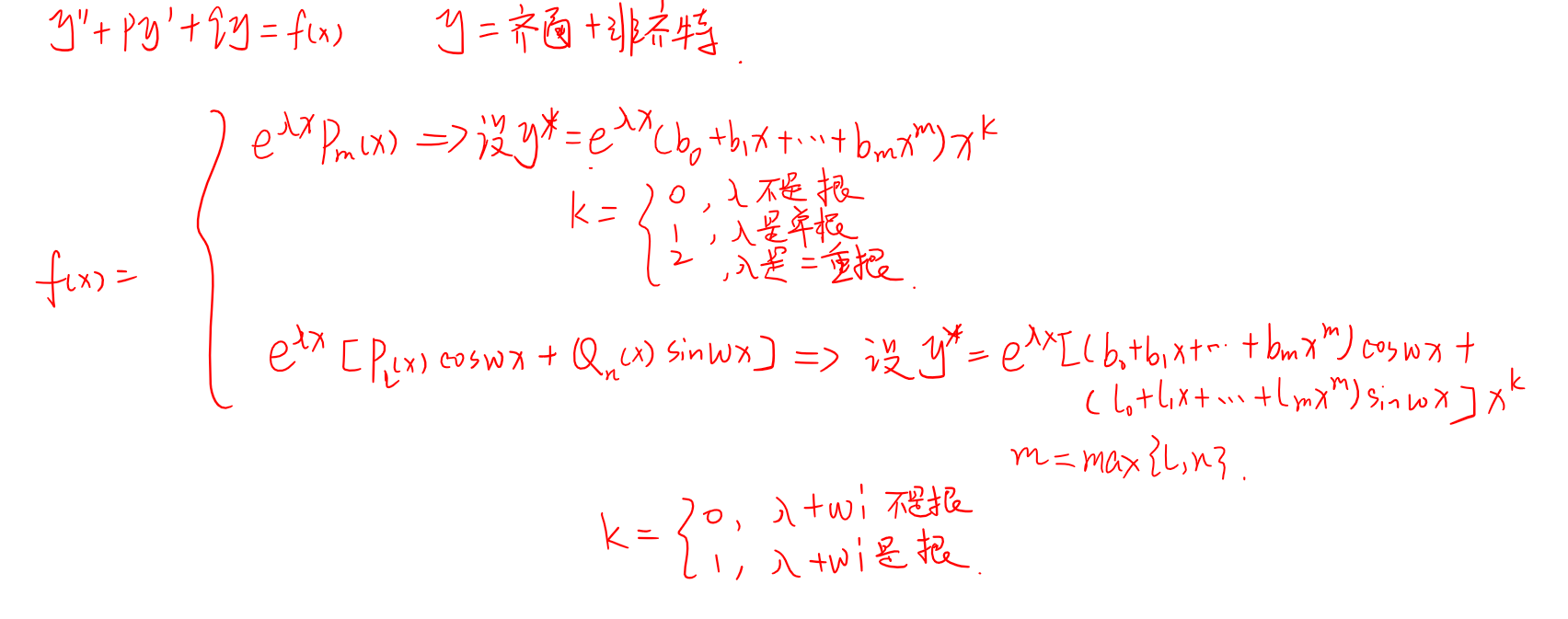
可降阶

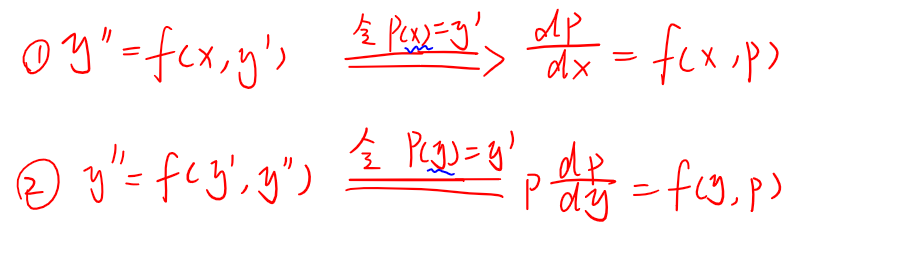
欧拉方程

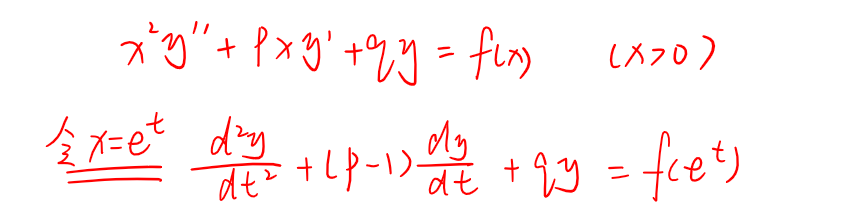
多元函数积分总结

三重积分

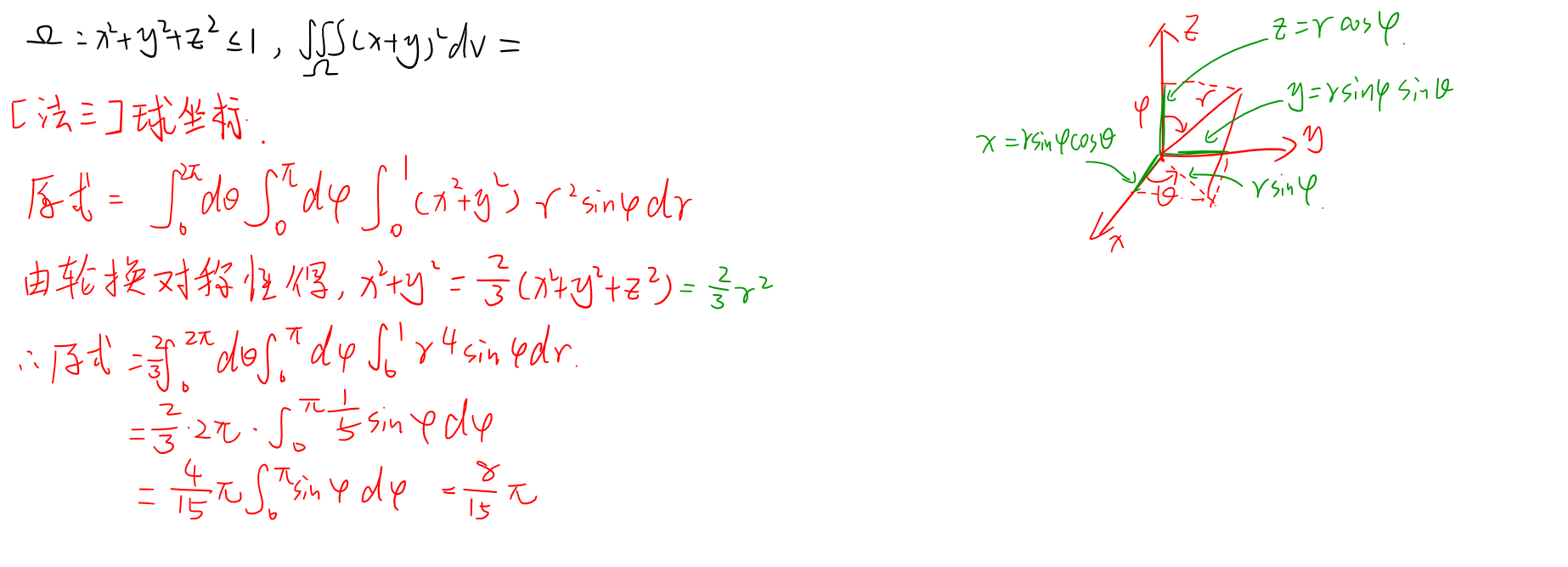
高斯公式

使用条件：

1. 曲面封闭
2. 函数可导（注意不可导点）

旋转曲面、投影曲面

格林公式

使用条件：

1. 封闭，正向（往曲线方向走时左手边）
2. 有一阶连续导数

斯托克斯公式

使用条件

1. 封闭，正向（右手法则，向上为正）
2. 有一阶连续导数

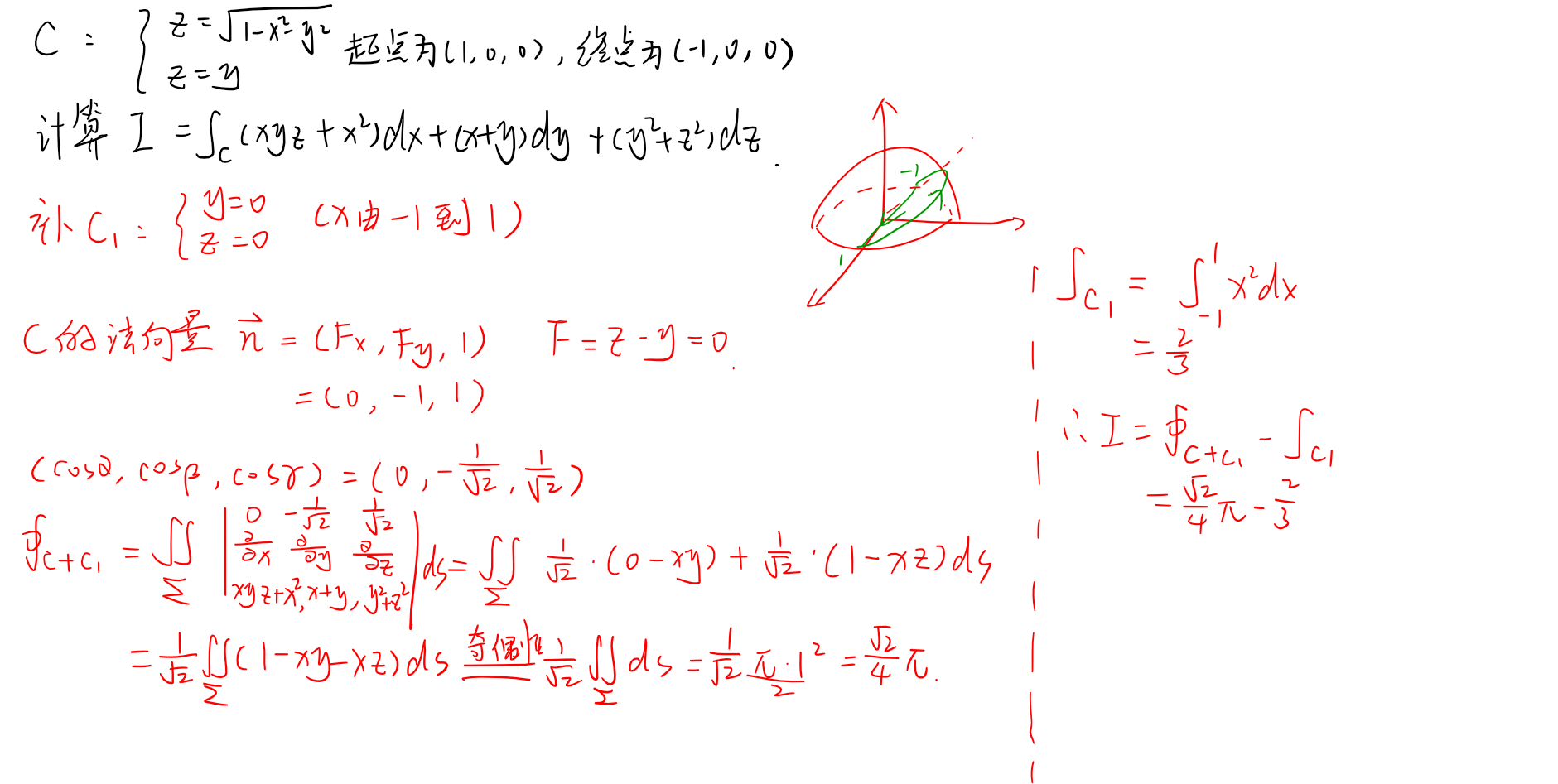
级数求和总结

整式型级数求和

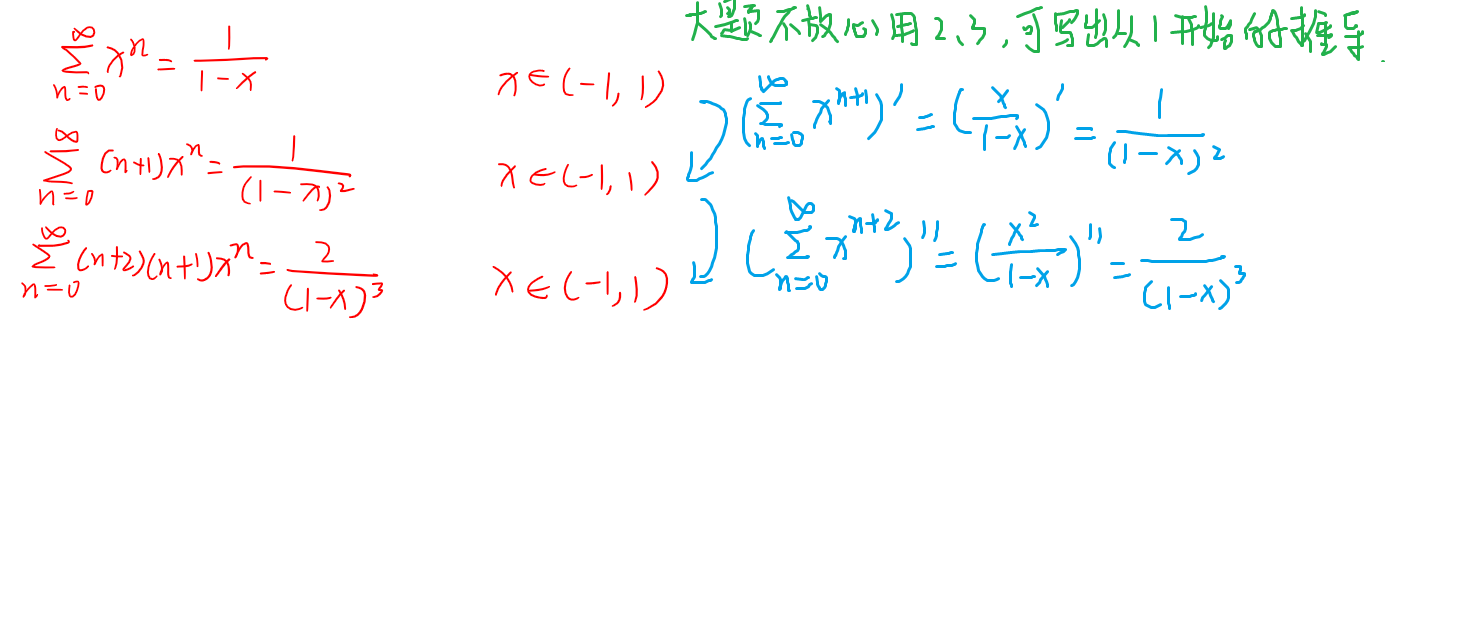
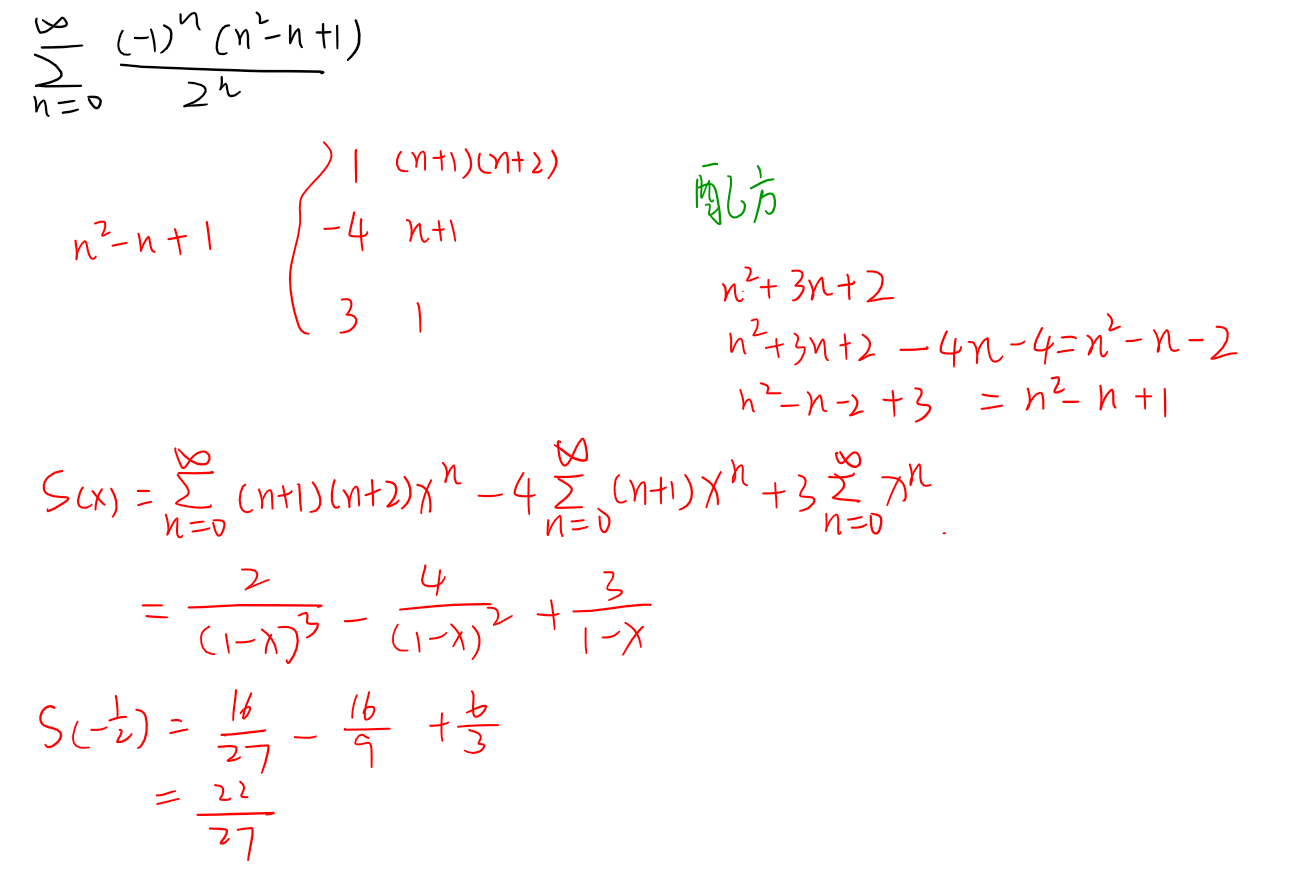
分式型级数求和

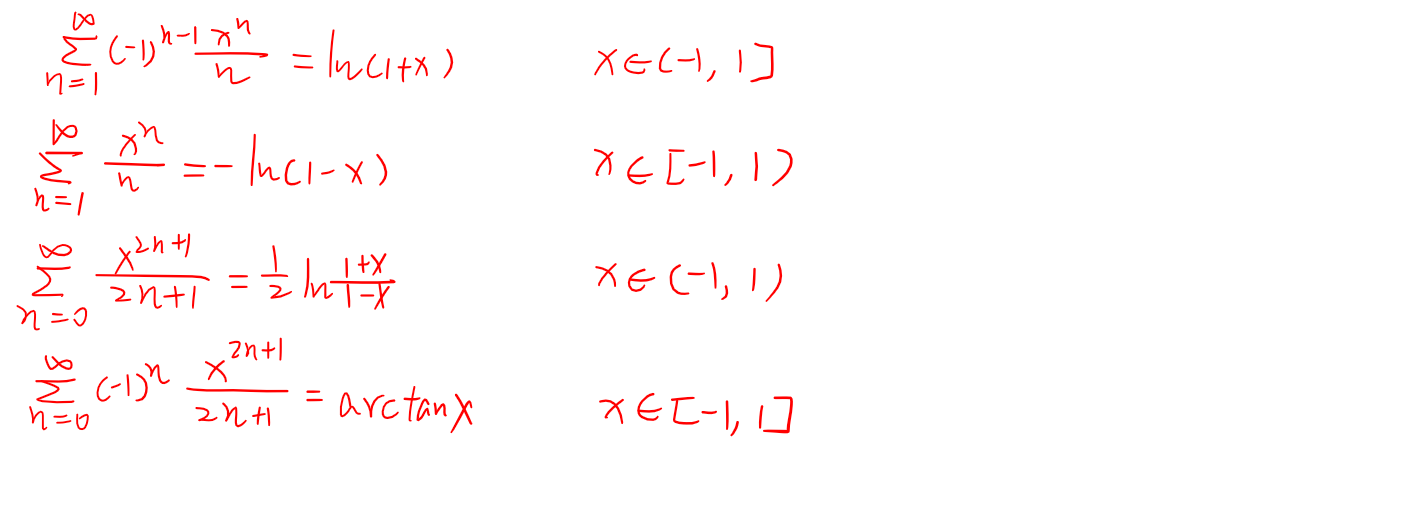
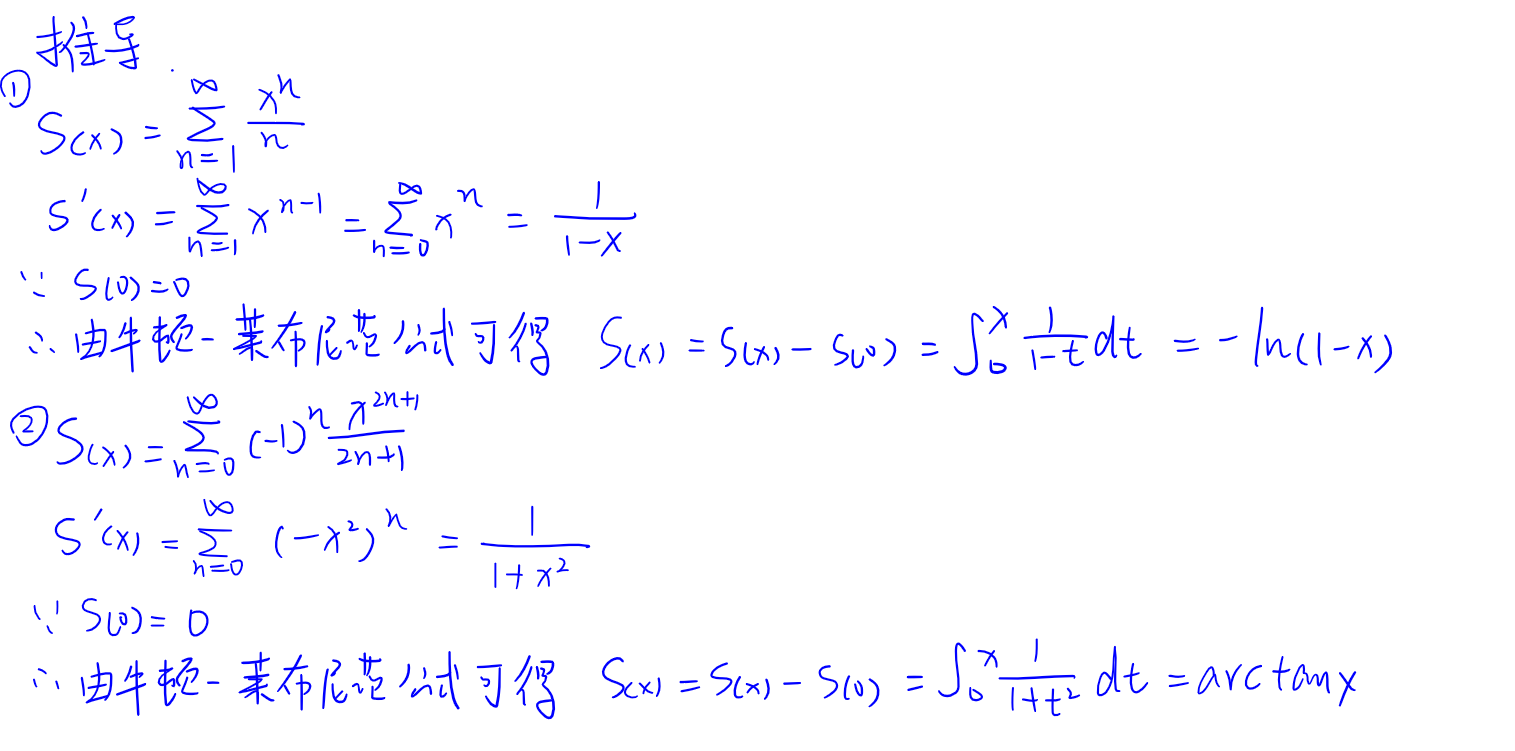
阶乘型级数求和

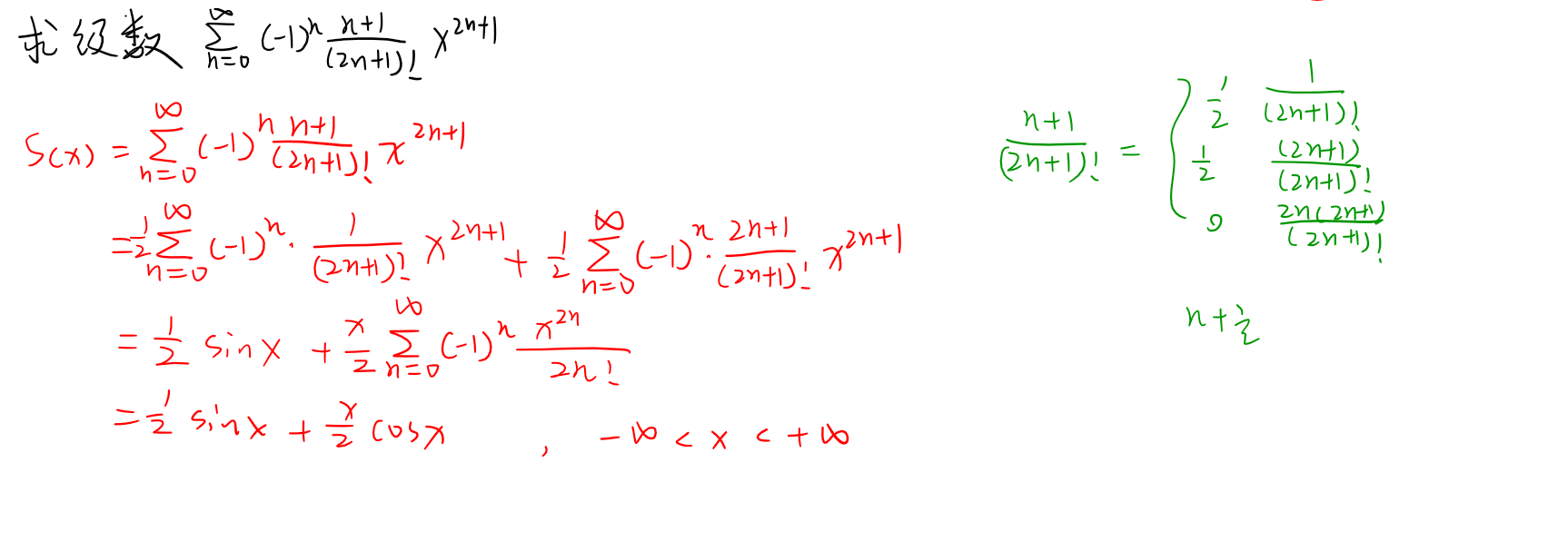
660

660(极限)

1-函数和定积分

补充题

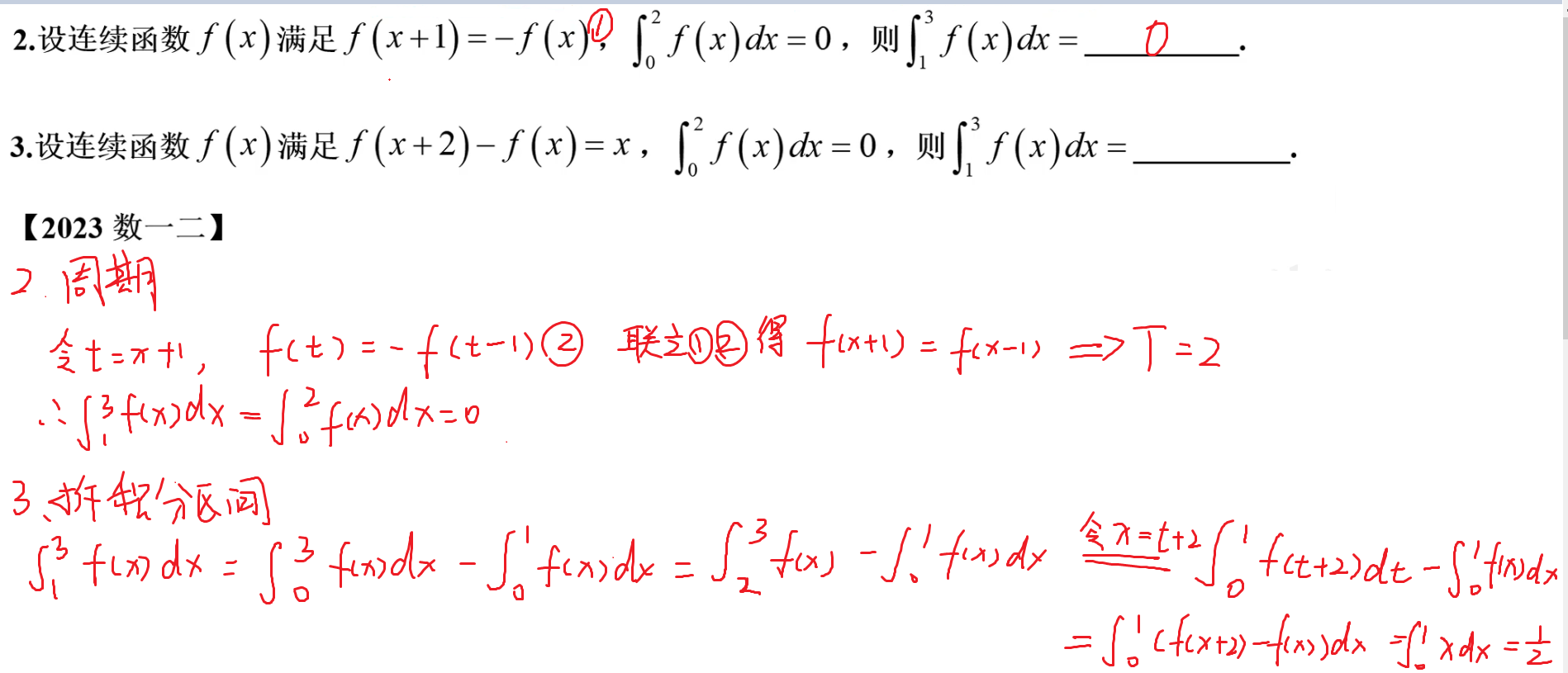
4-1的∞次方型

1的∞次方、∞的0次方、0的0次方都用这种方法做

5-∞-∞型

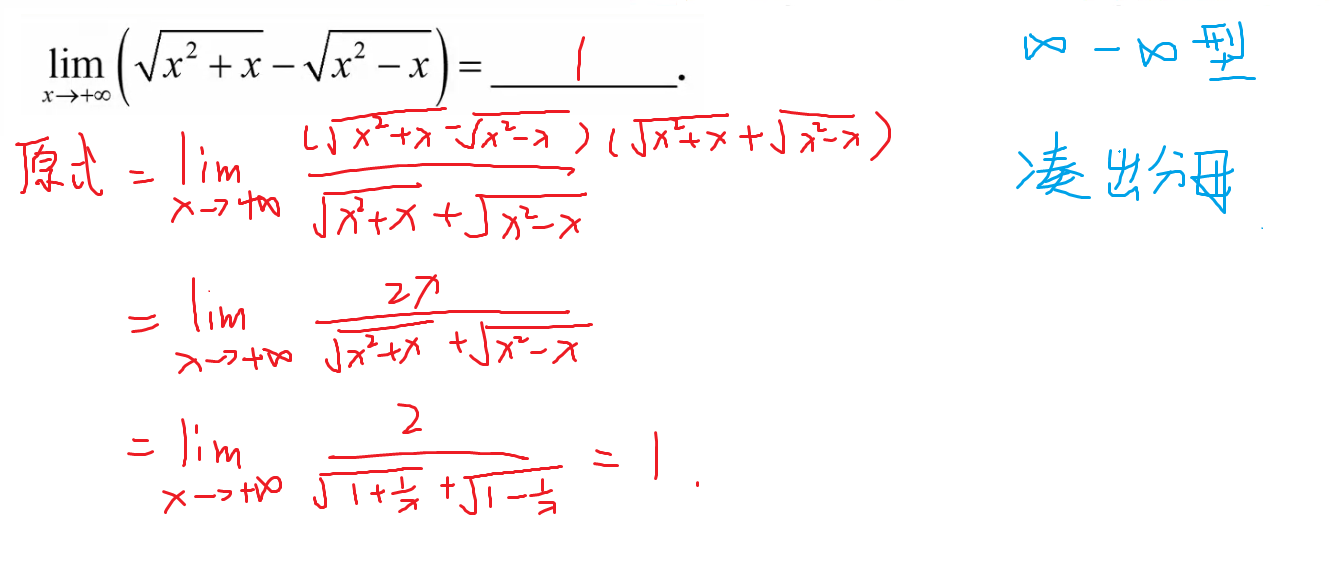
6-泰勒公式计算极限

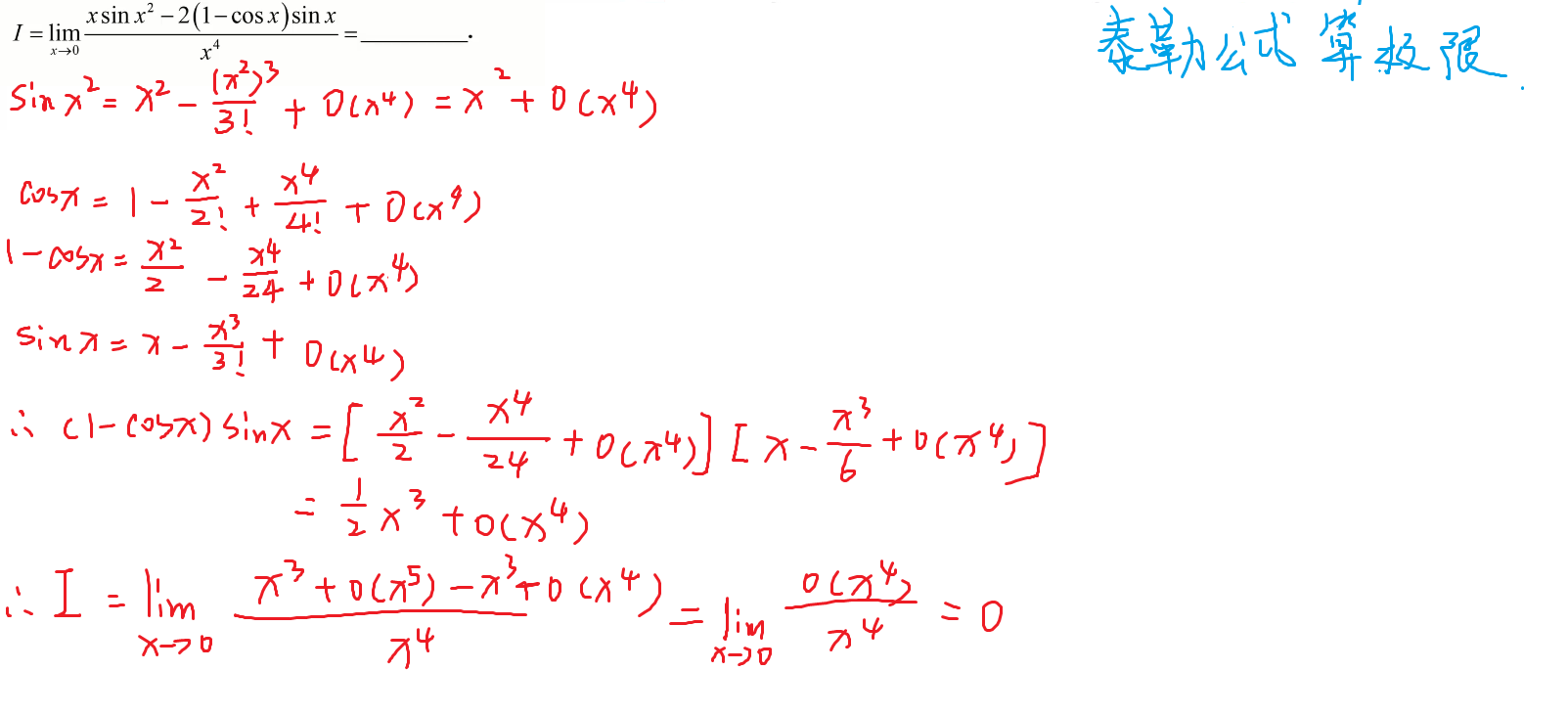
7-可爱因子

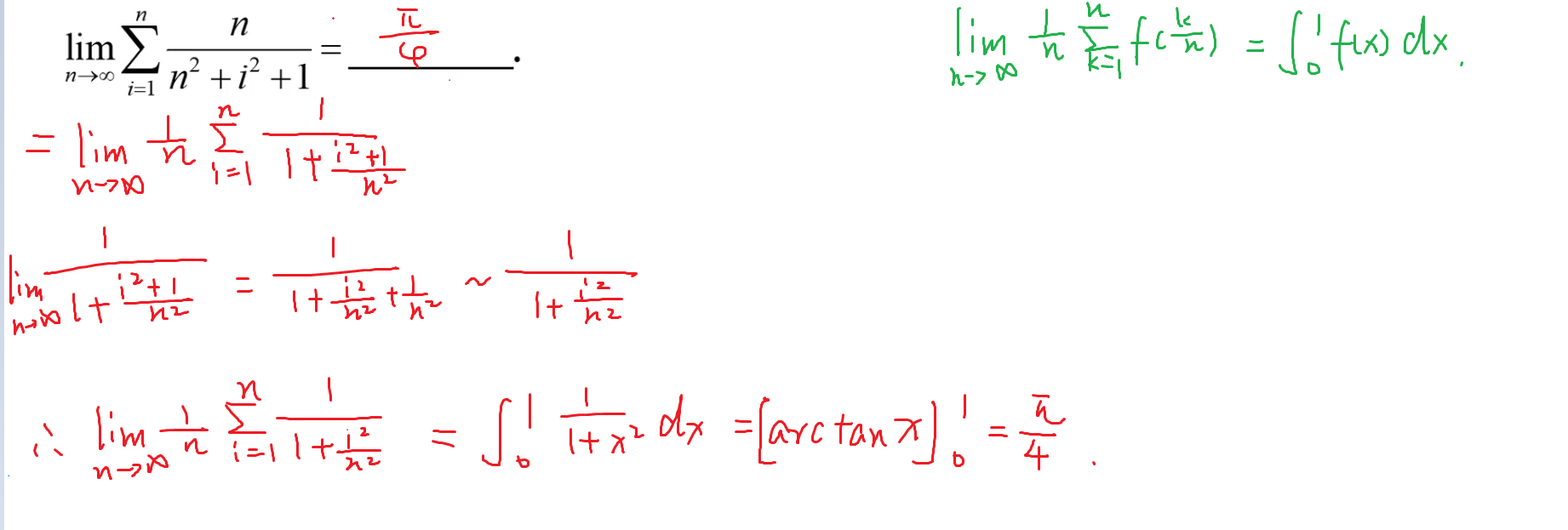
补充题目

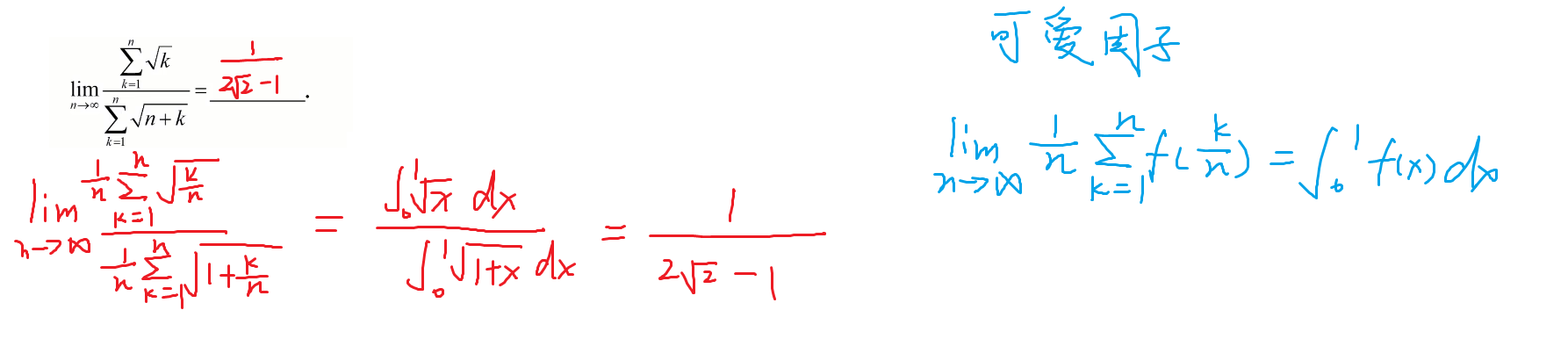
10-底数相同的情况

补充题目

12-拉格朗日中值定理

15-左右极限

补充题目

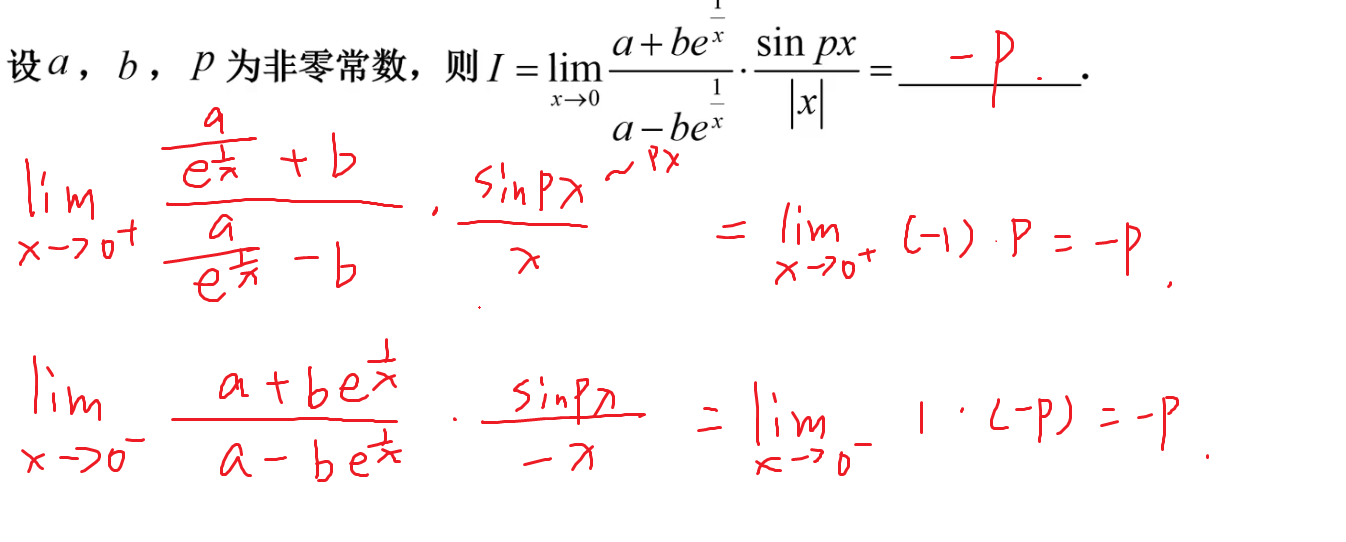
17-泰勒展开

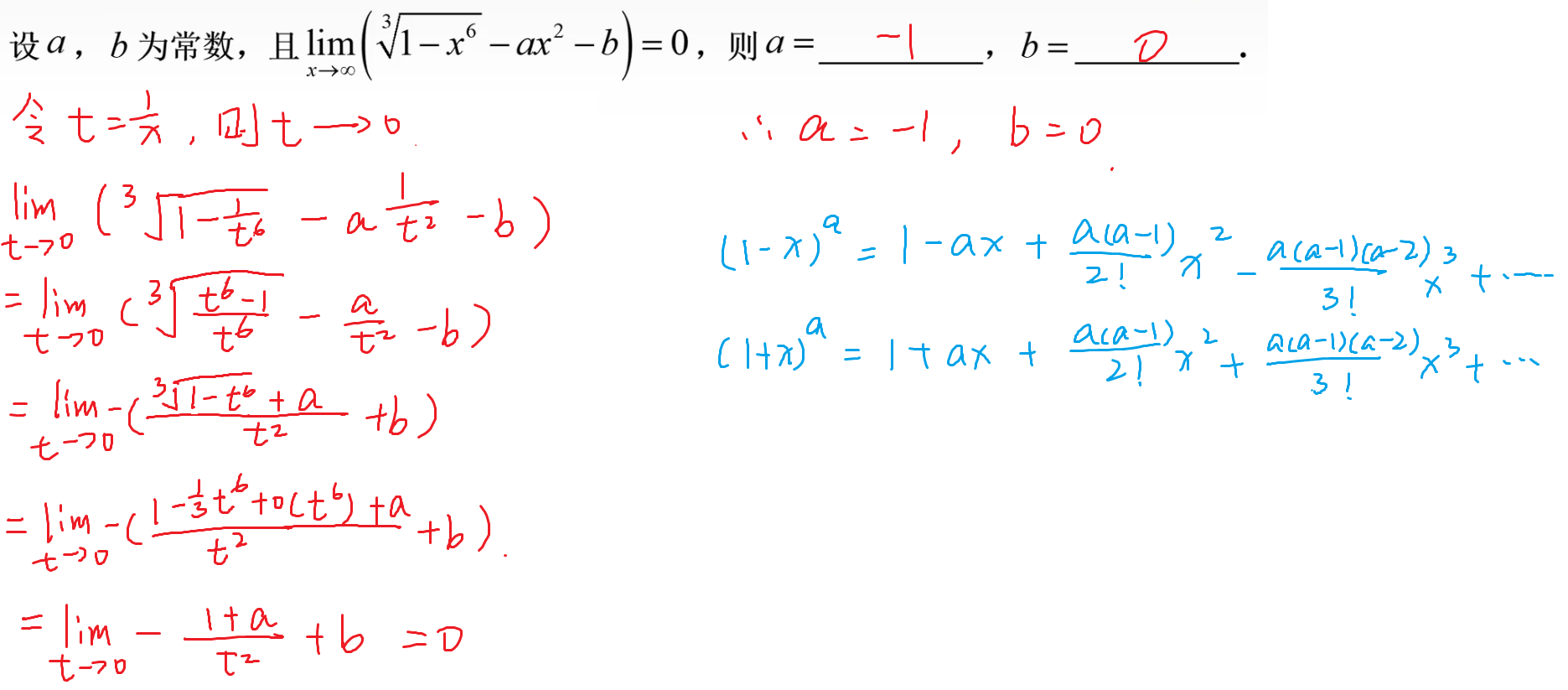
补充题目

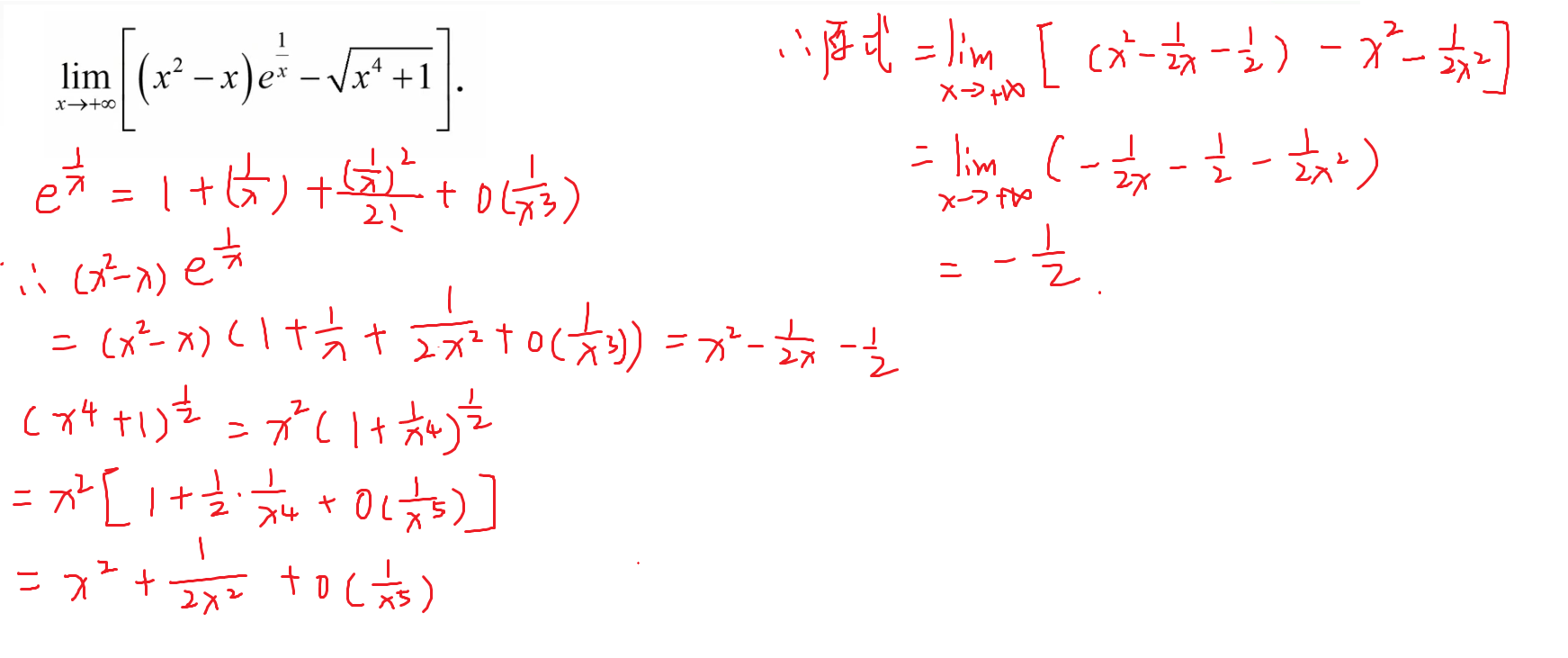
19

25-函数连续性

补充题目

126-夹逼定理

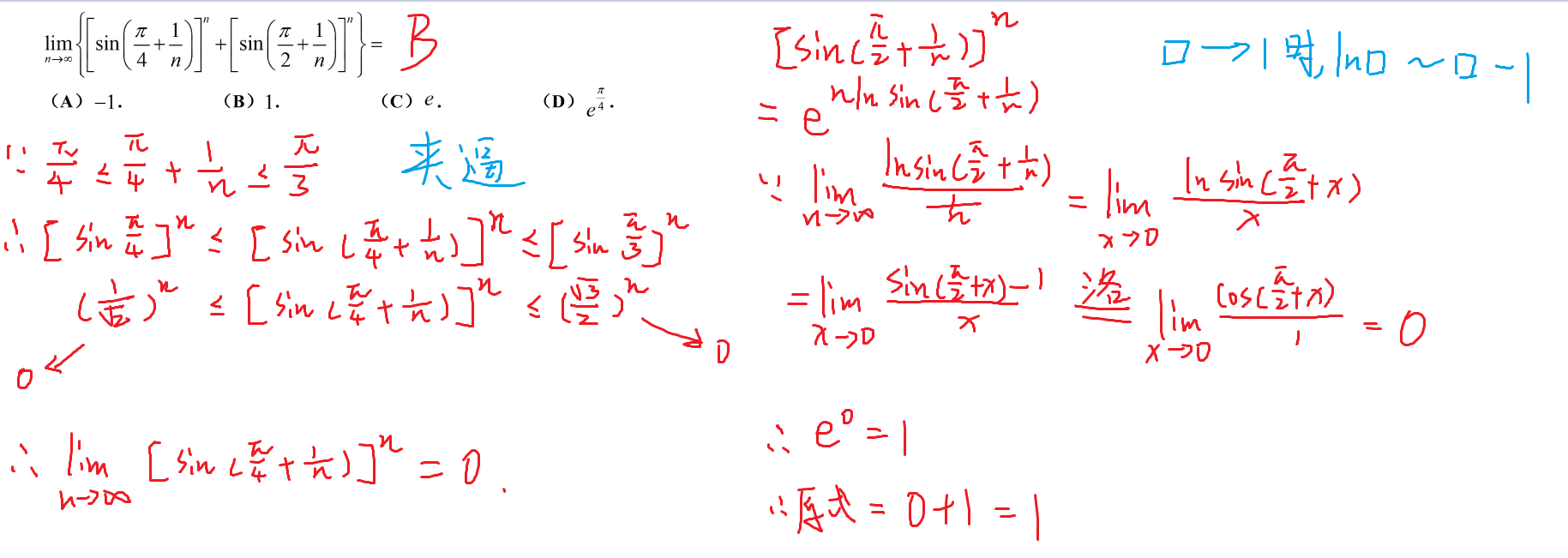
128-常见不等式

补充知识点

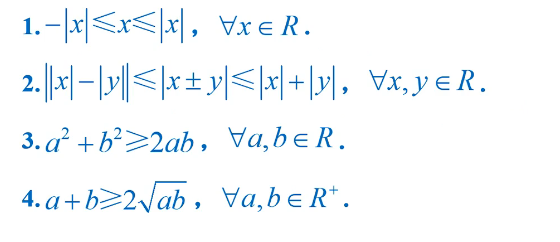
132-和差化积

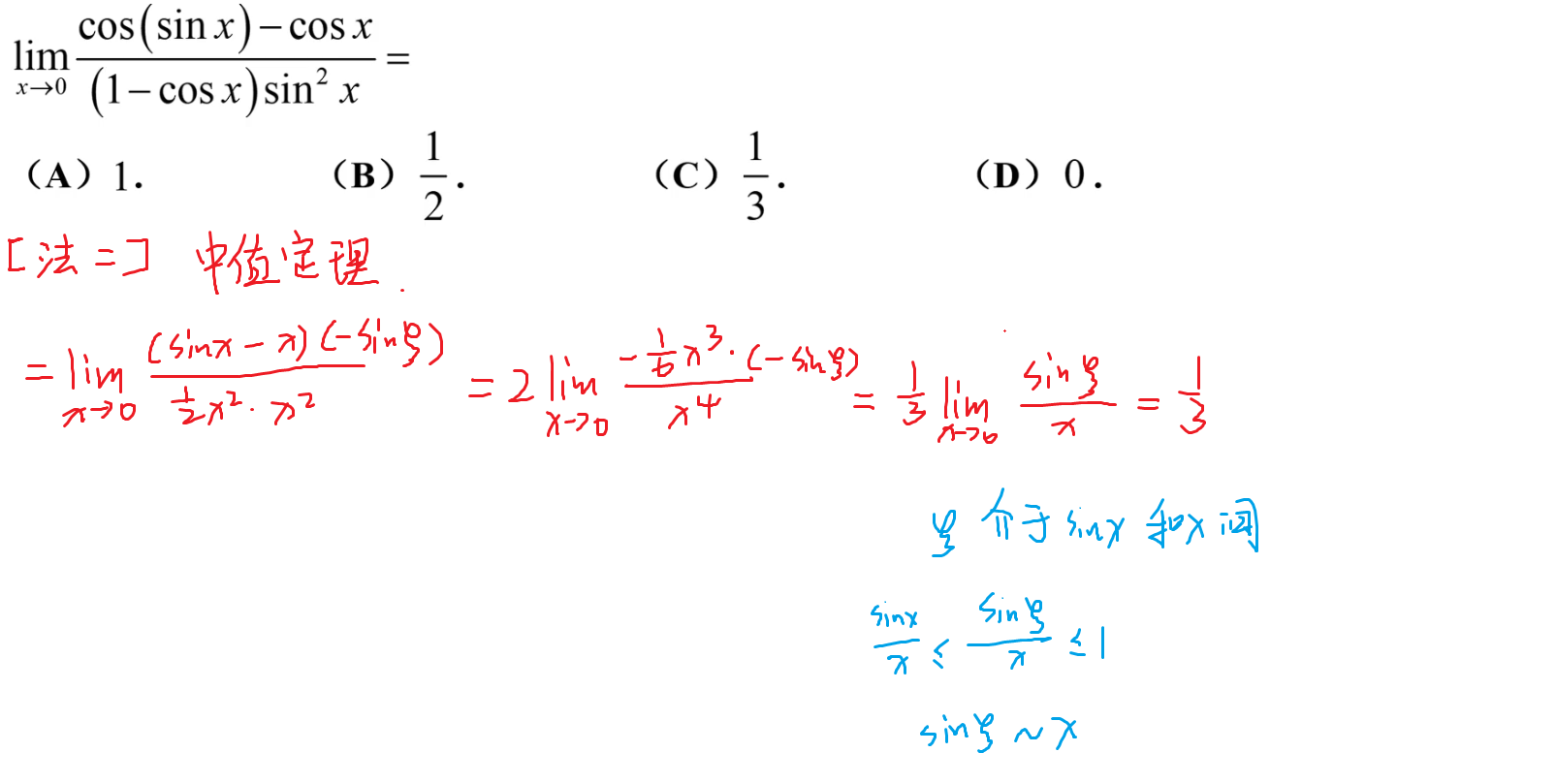
补充知识点

135-极限和无穷小的关系

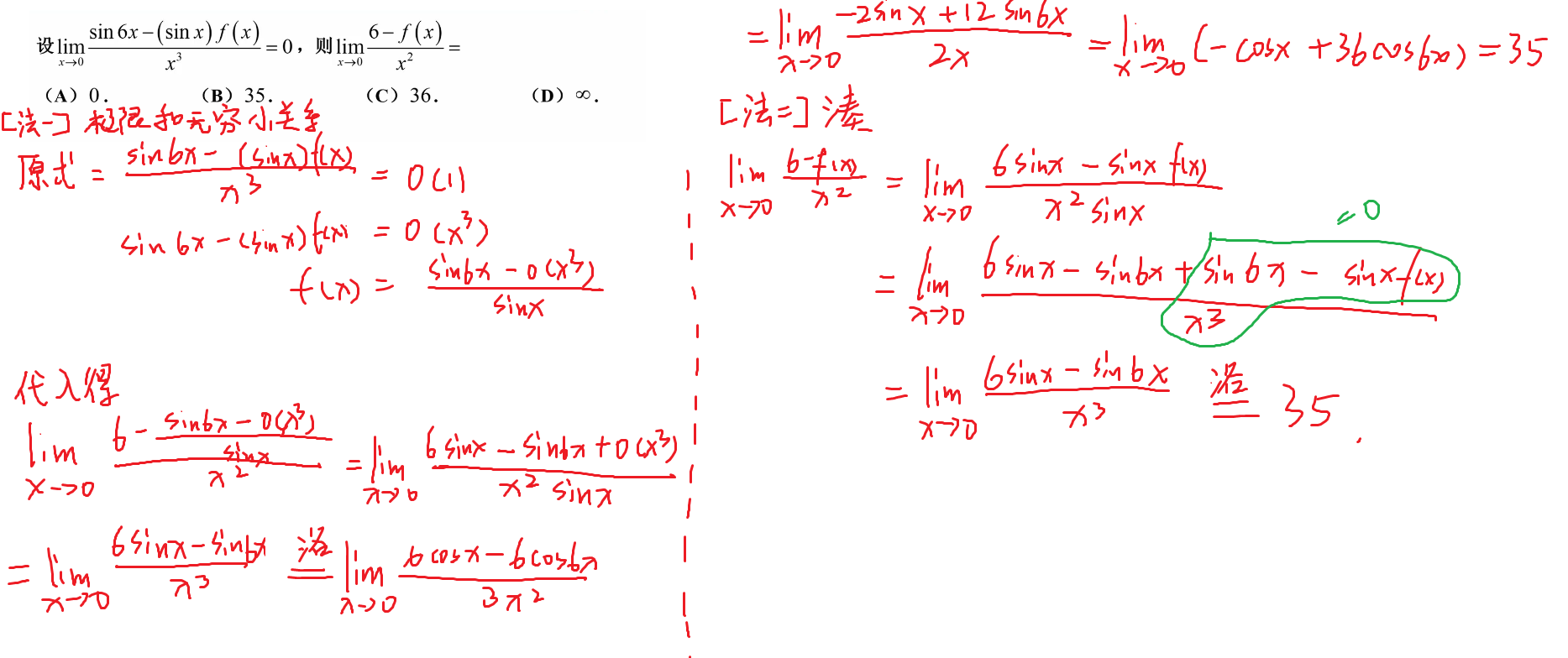
137-放缩求值

138-等价无穷小

147-母0子必0

150-导数周期

152-泰勒展开的两种形式

补充题目

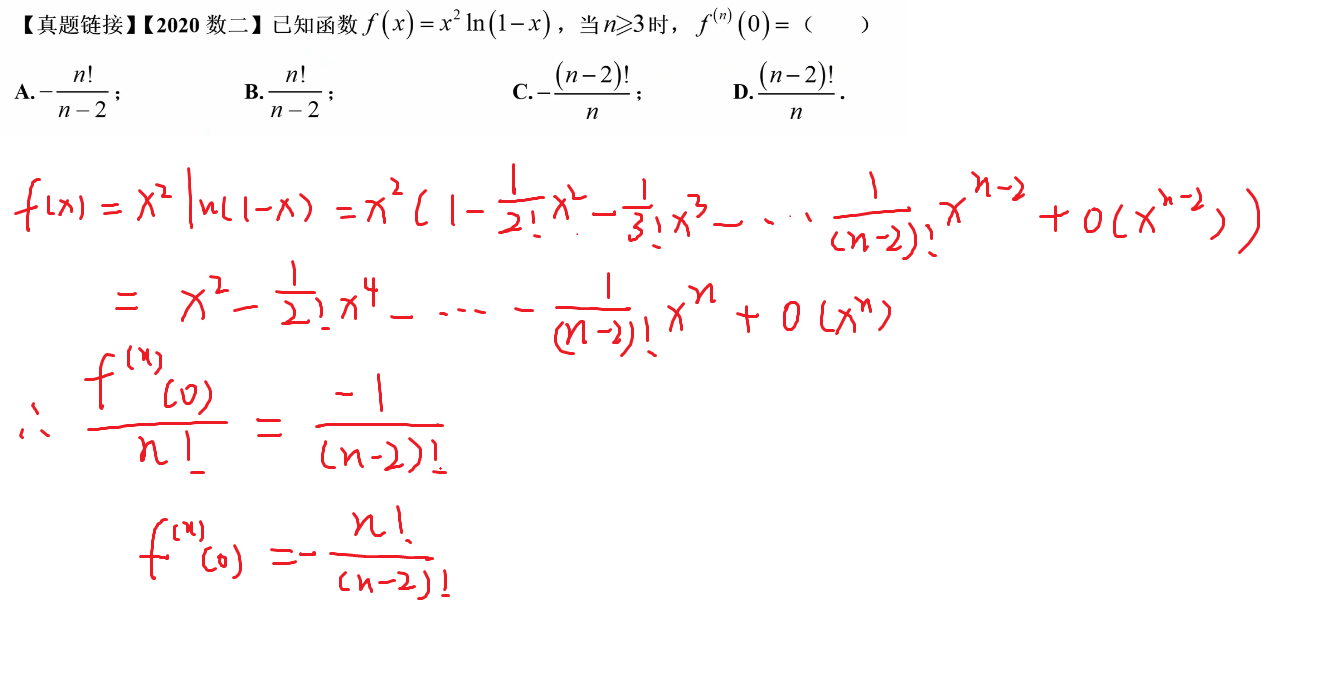
154-导数和导数极限的关系

补充知识点

168-导数和原函数有界无界

173-讨论函数大小关系

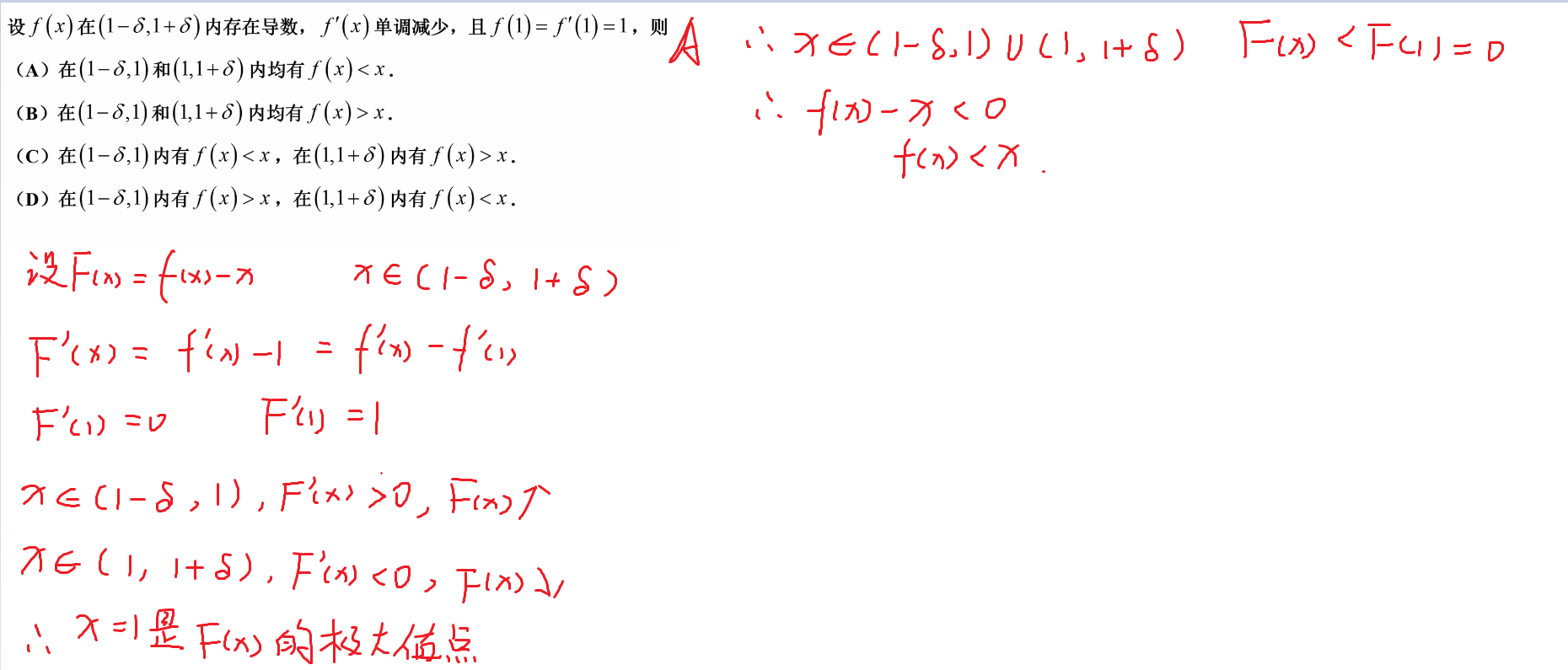
补充题目

174-渐近线

补充题目

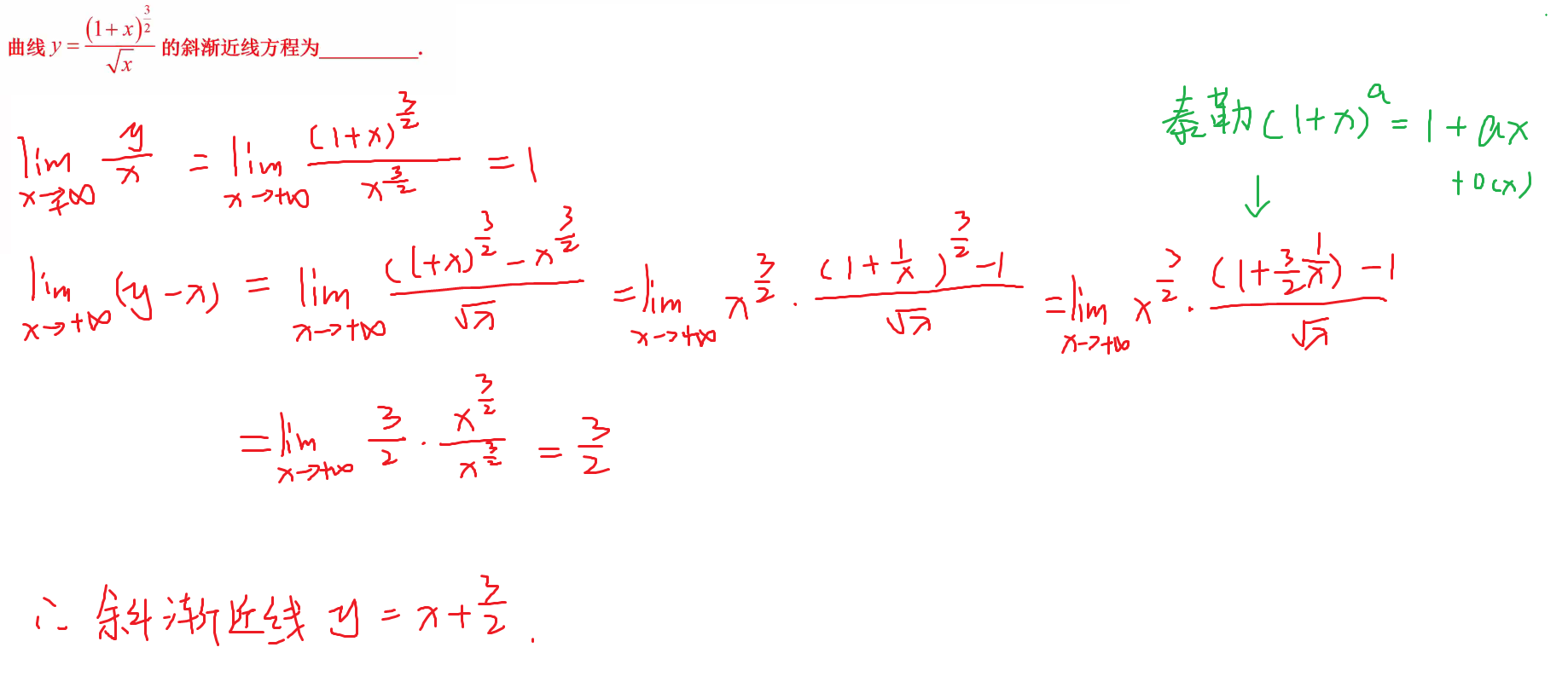
660(积分)

29-导数定义

补充题目

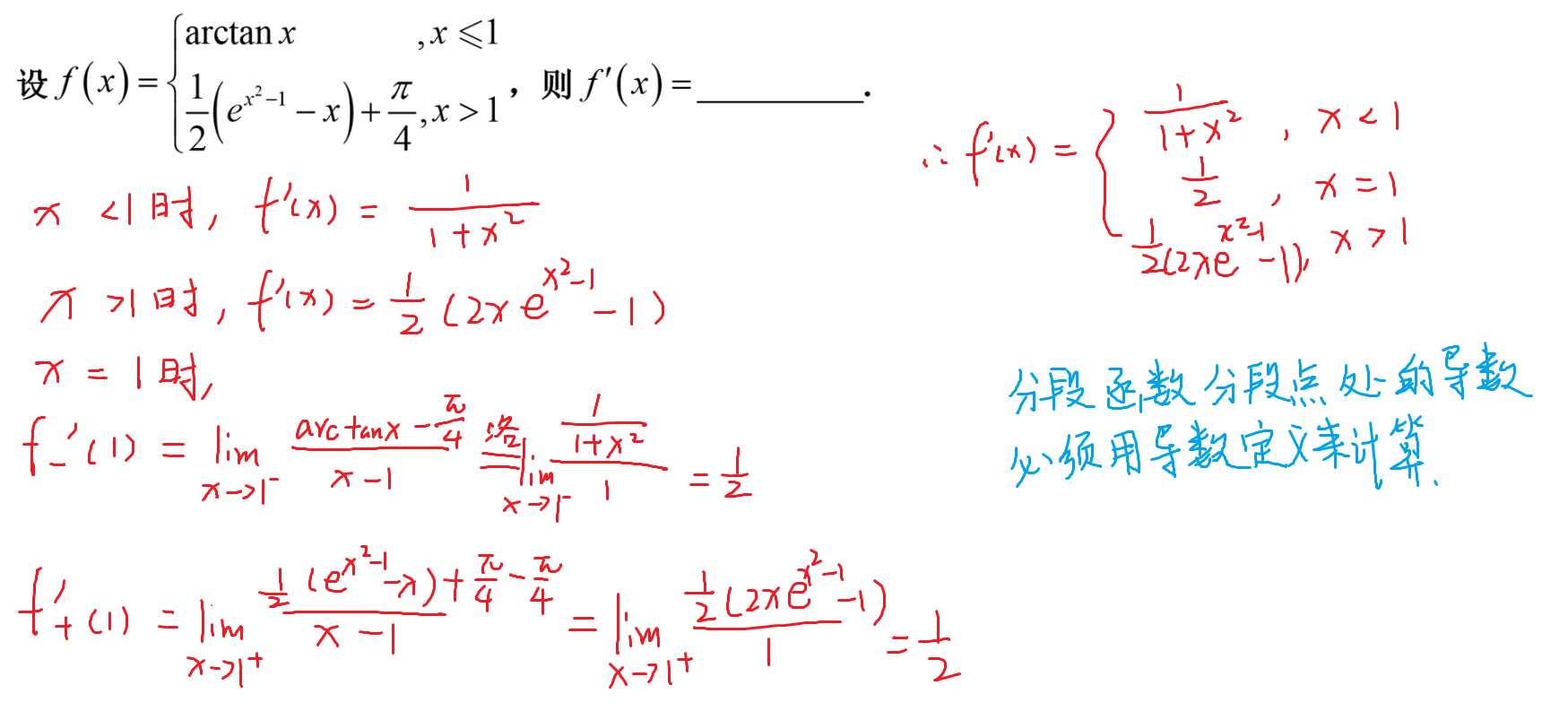
34-曲率

39-复合函数求导

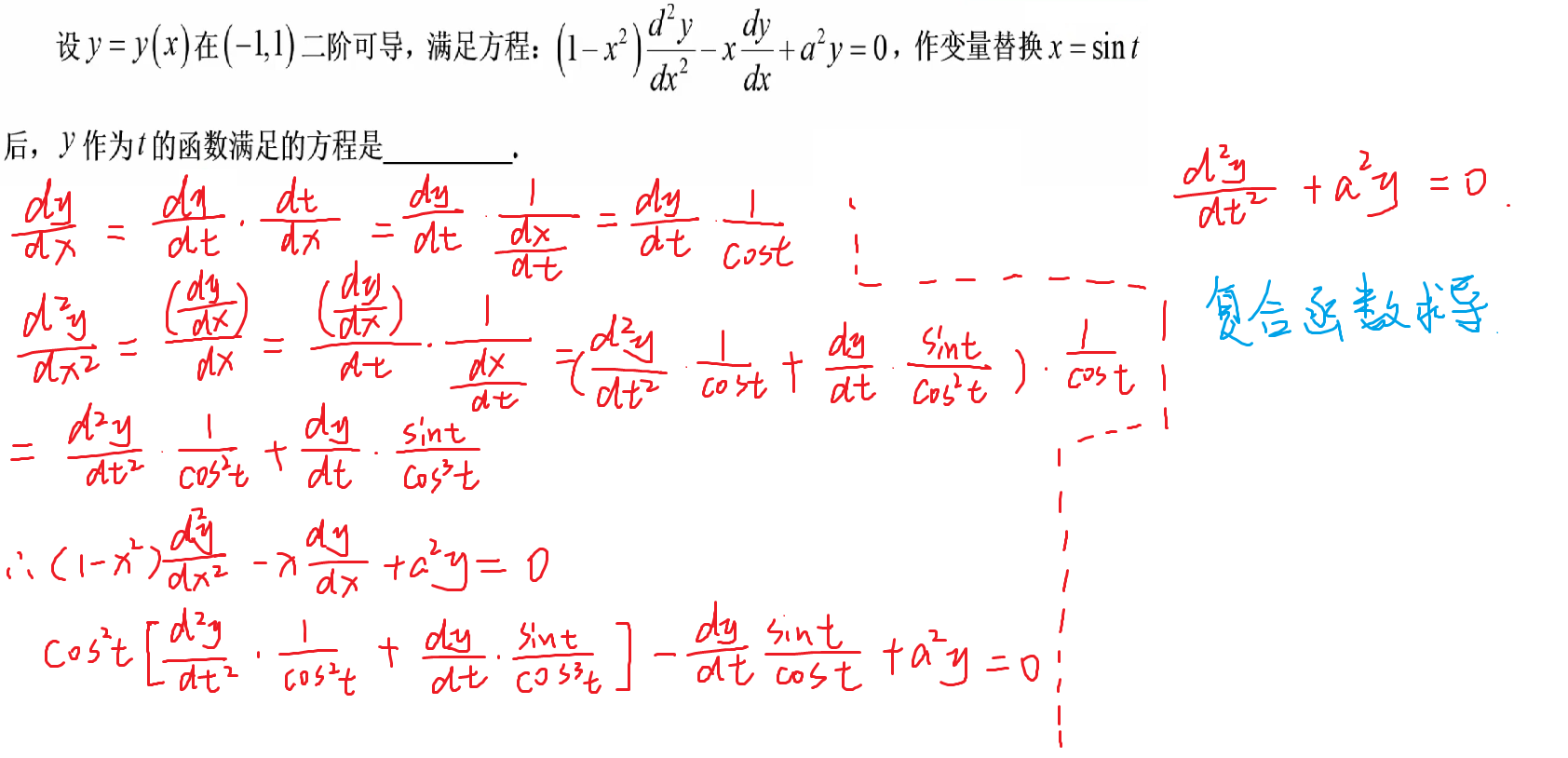
补充题目

41-曲率半径

42-驻点

52-积分

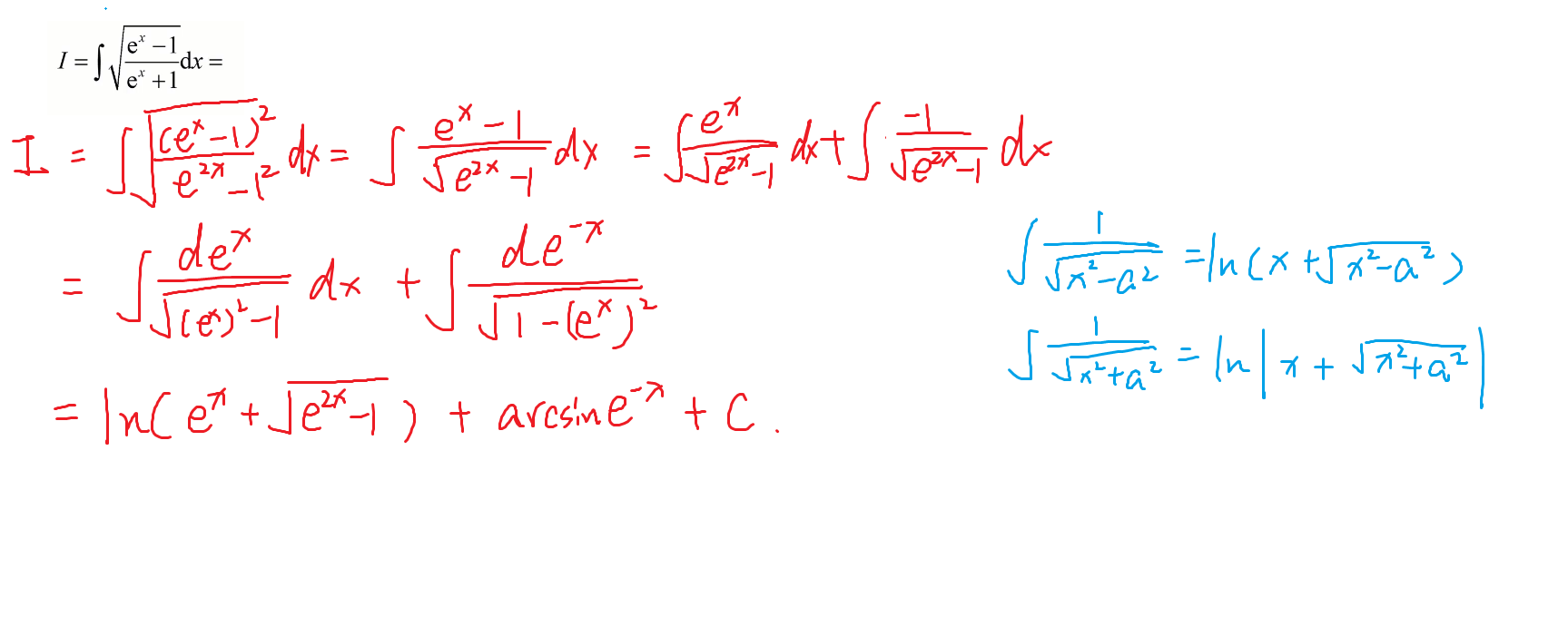
57-二倍角公式

60-积分换元

61-周期

64-区间在现

补充题目

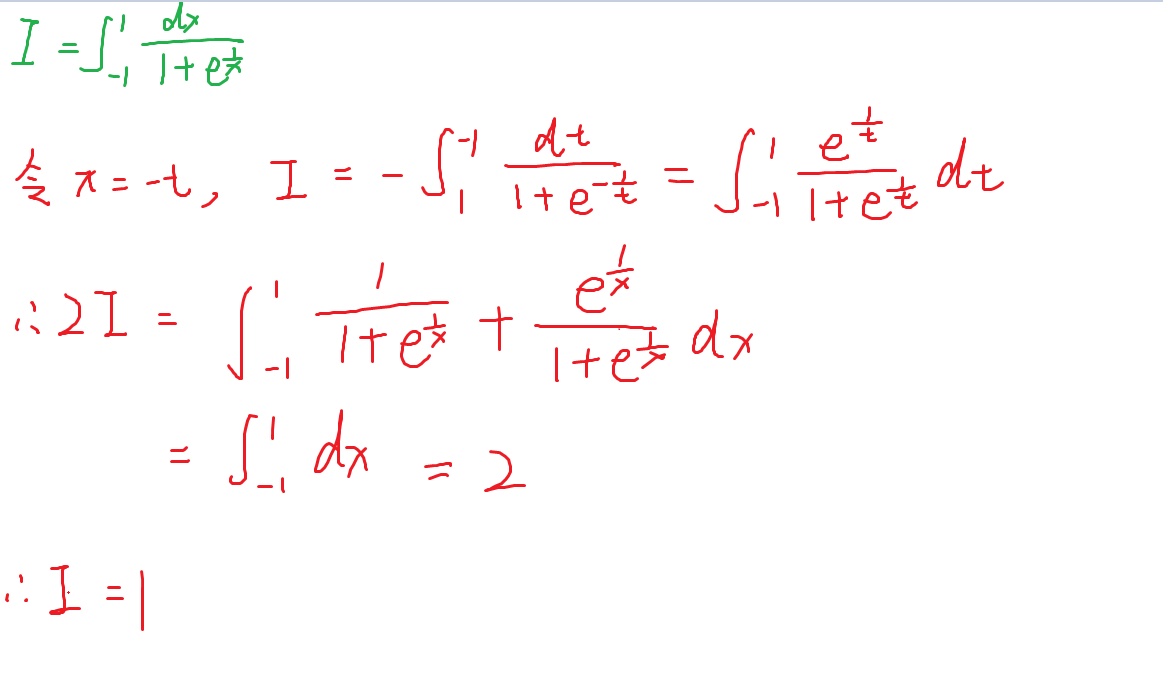
69-反常积分

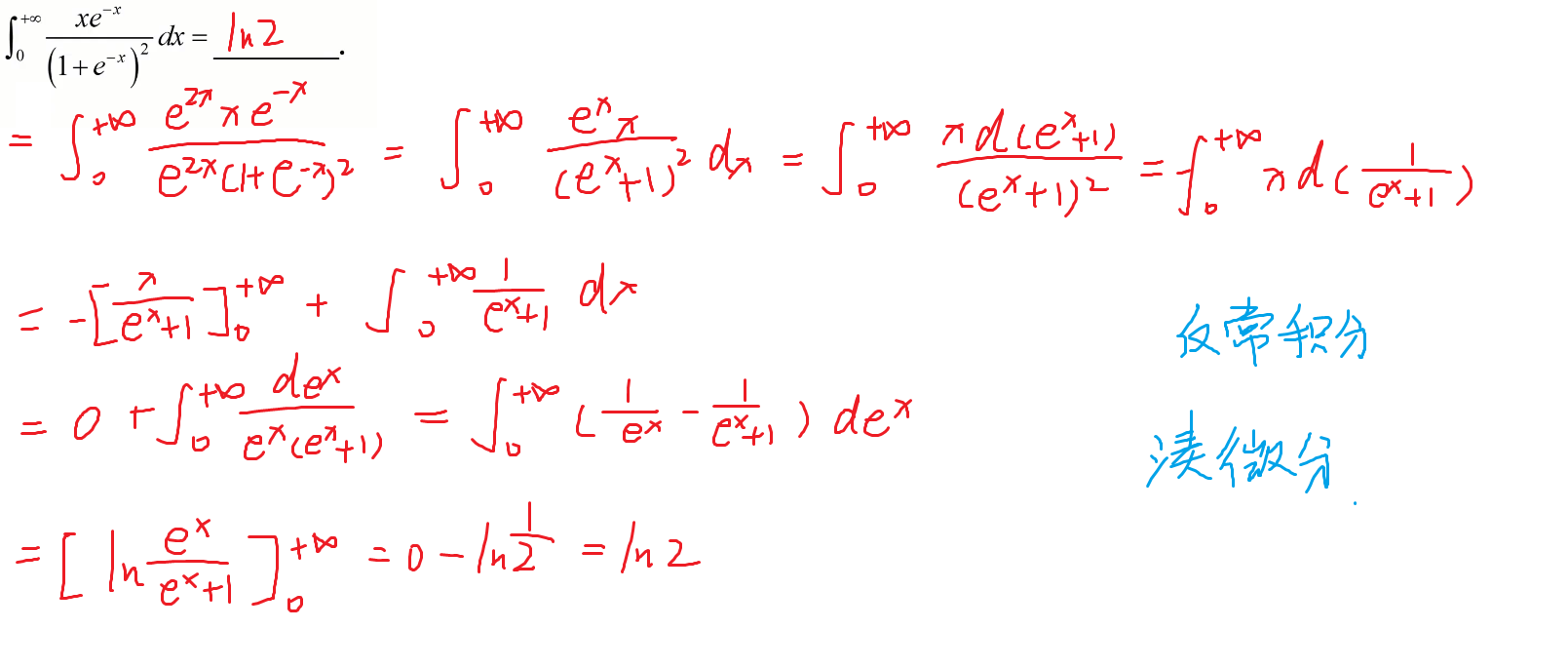
70-摆线

70-积分几何应用

73-质心

74-物理应用

176-原函数

177-积分性质

181-积分性质

补充题目

183-定积分比大小

总结

184-定积分比大小奇偶性化简

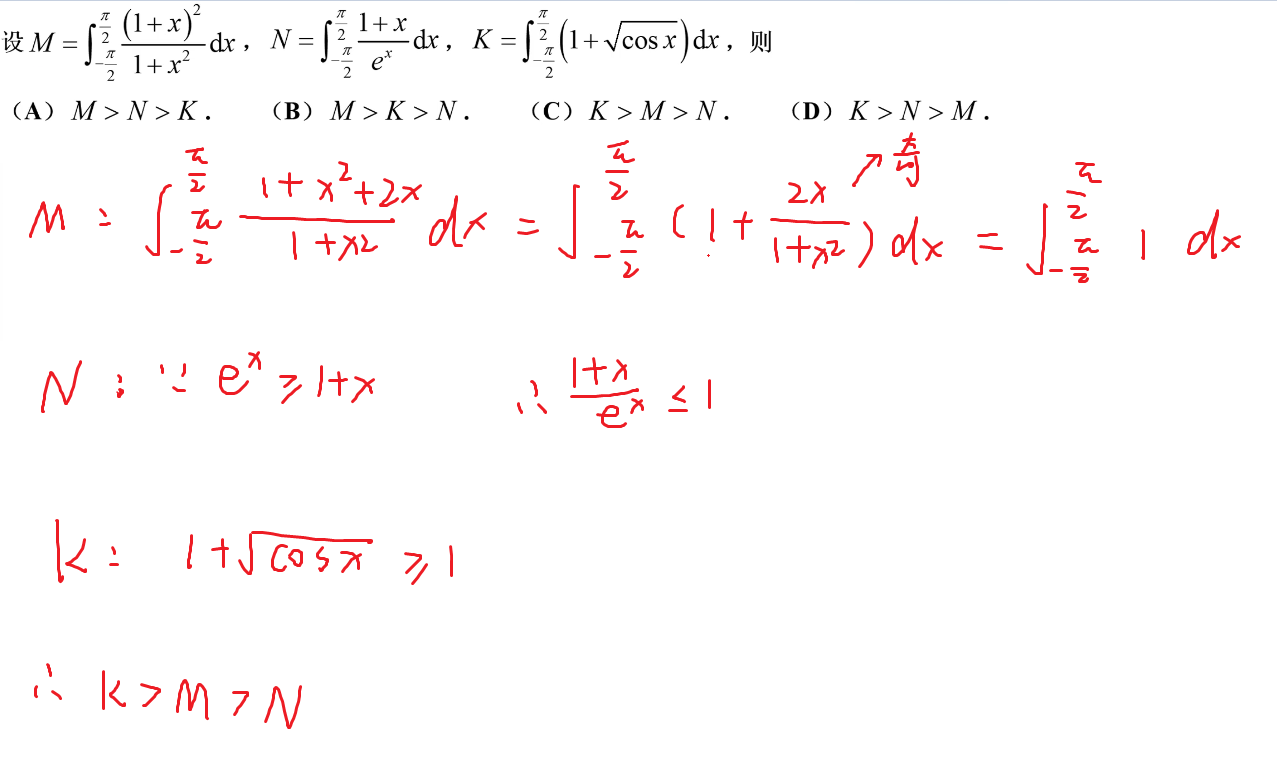
186-莱布尼茨公式注意事项

、

188-定积分计算

补充题目

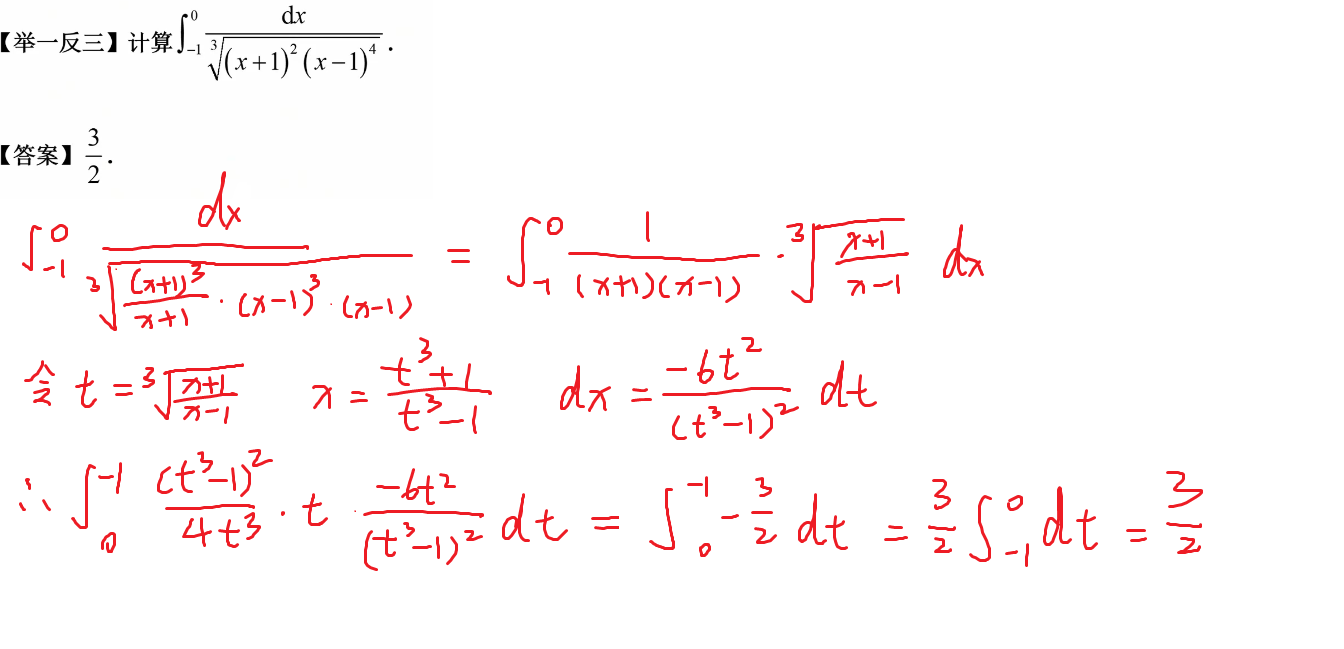
199-原函数存在条件

203-反常积分审敛

208-平面曲线质心

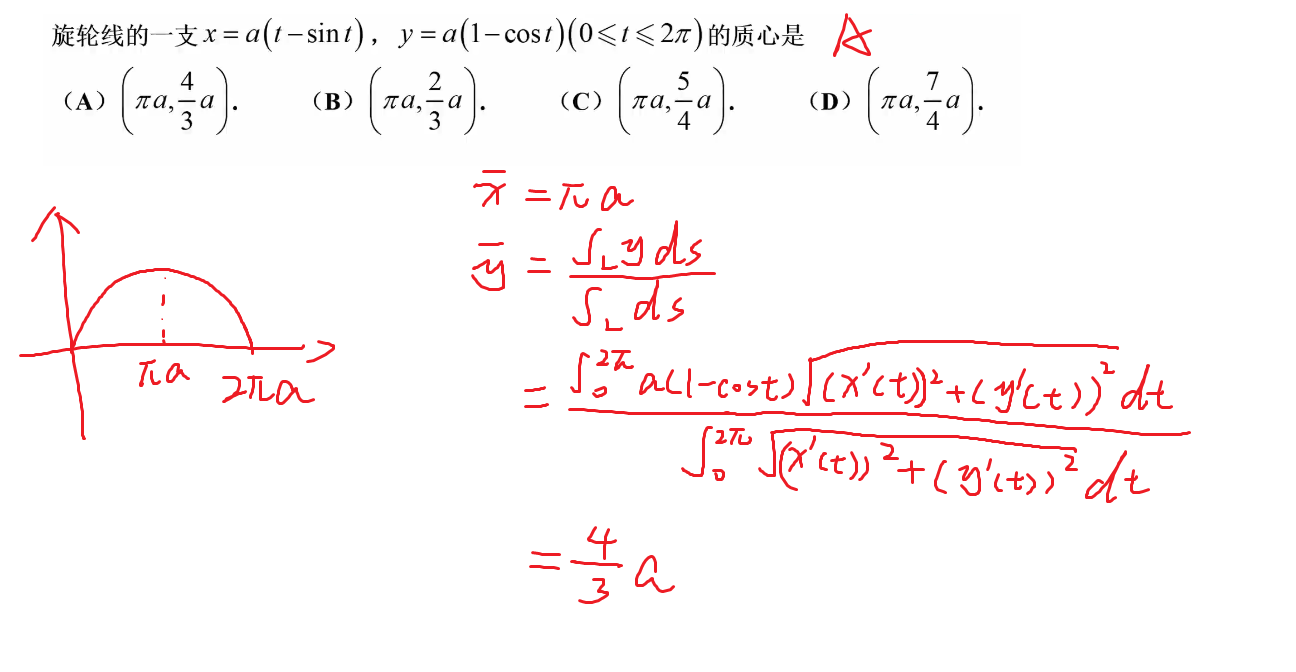
补充题目

660(微分方程)

76-一阶线性微分方程通解

78-y/x型齐次方程

79 -自因变量互换

80-二阶降阶

81-常系数非齐次求特解

知识点

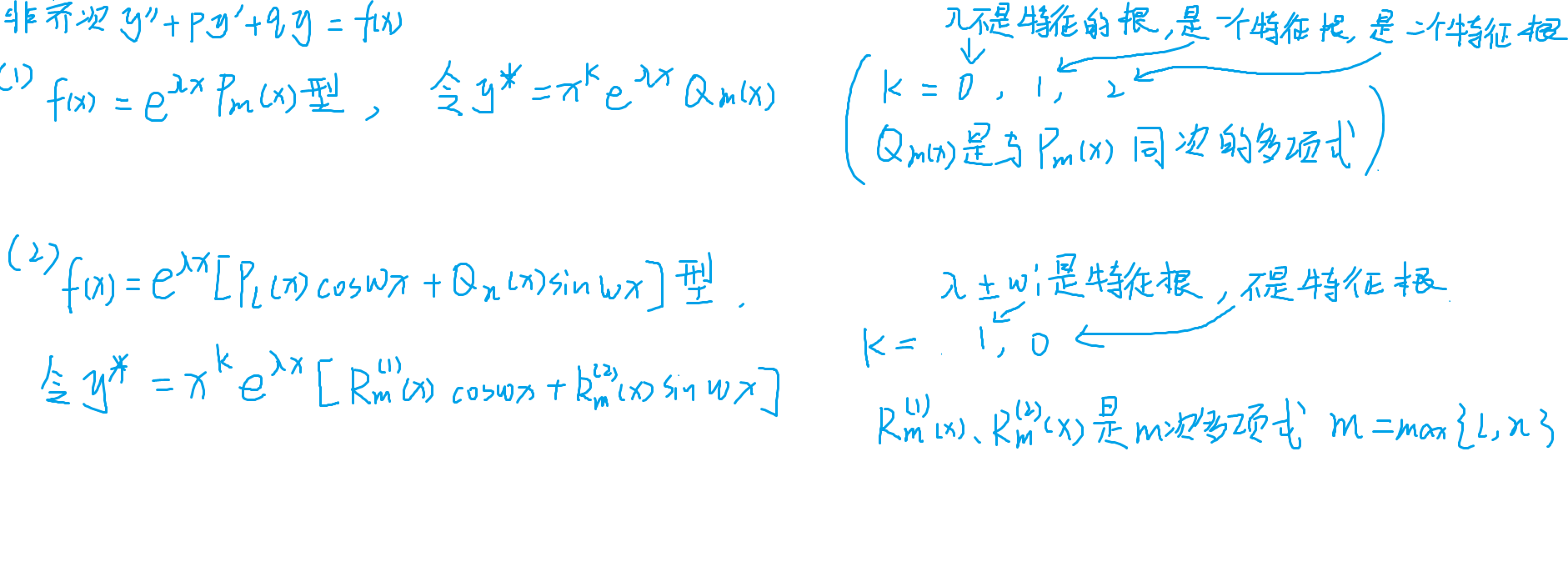
86-偏导化为普通导数

90-复合函数求偏导

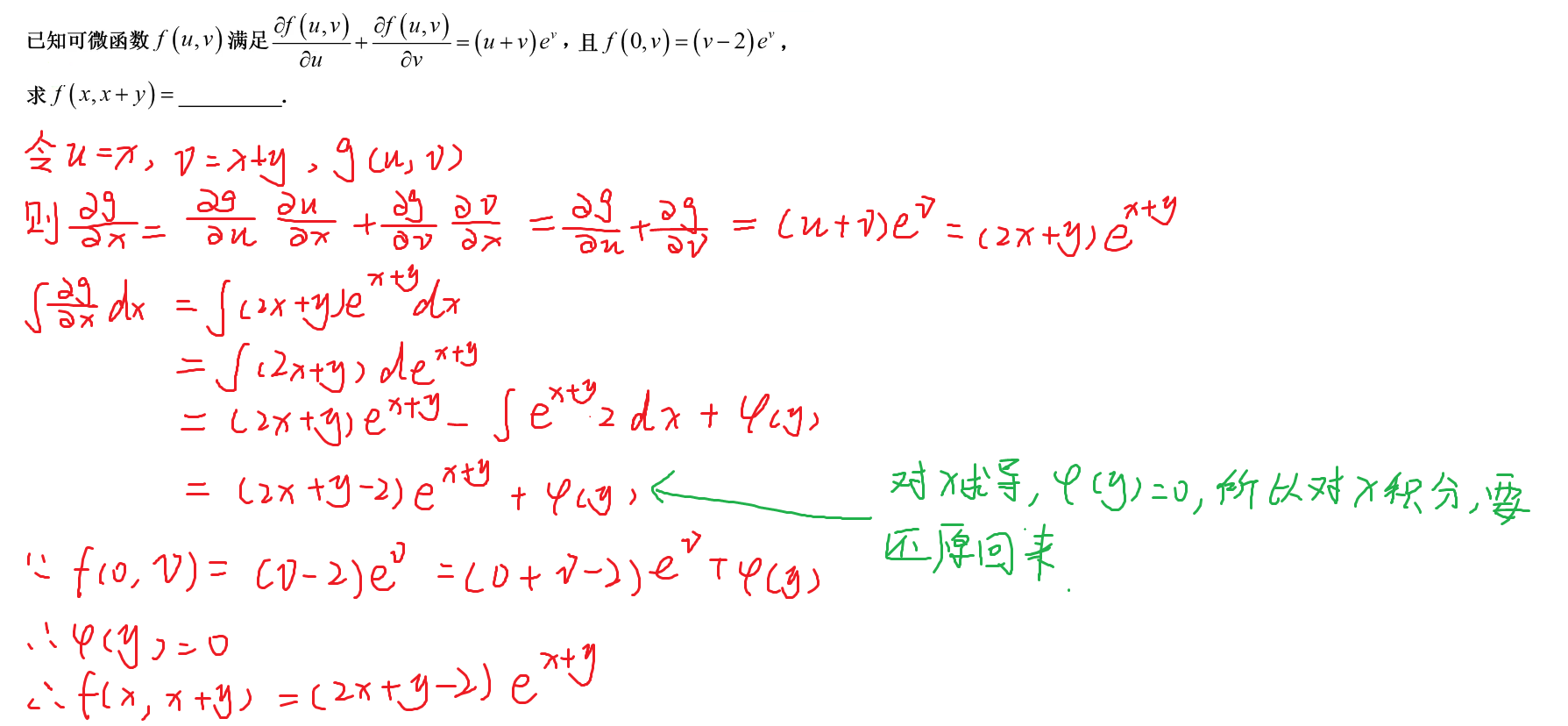
补充题目

91-混合偏导

补充题目

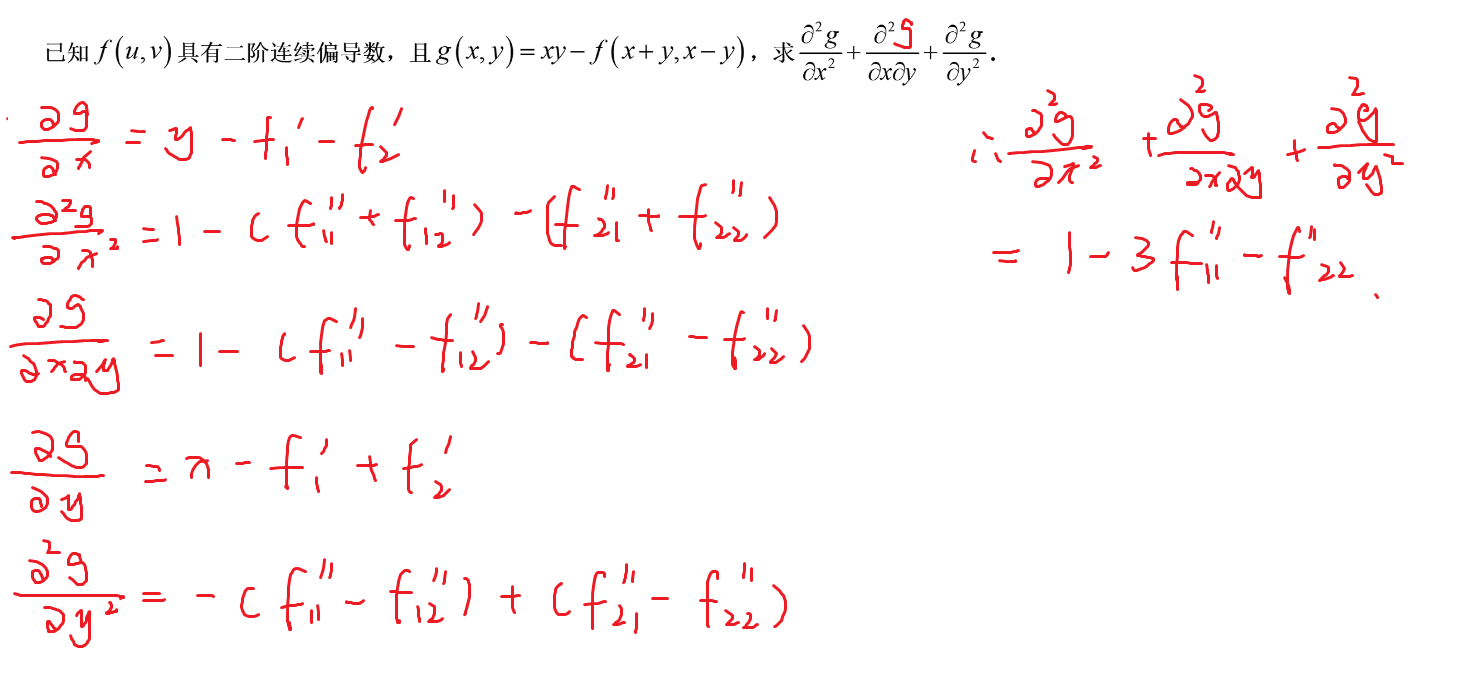
92-链式求导

补充题目

101-求全微分

补充题目

104-多元函数求极值

217-叠加原理

223-伯努利方程

224-求全微分

225-欧拉方程

推导

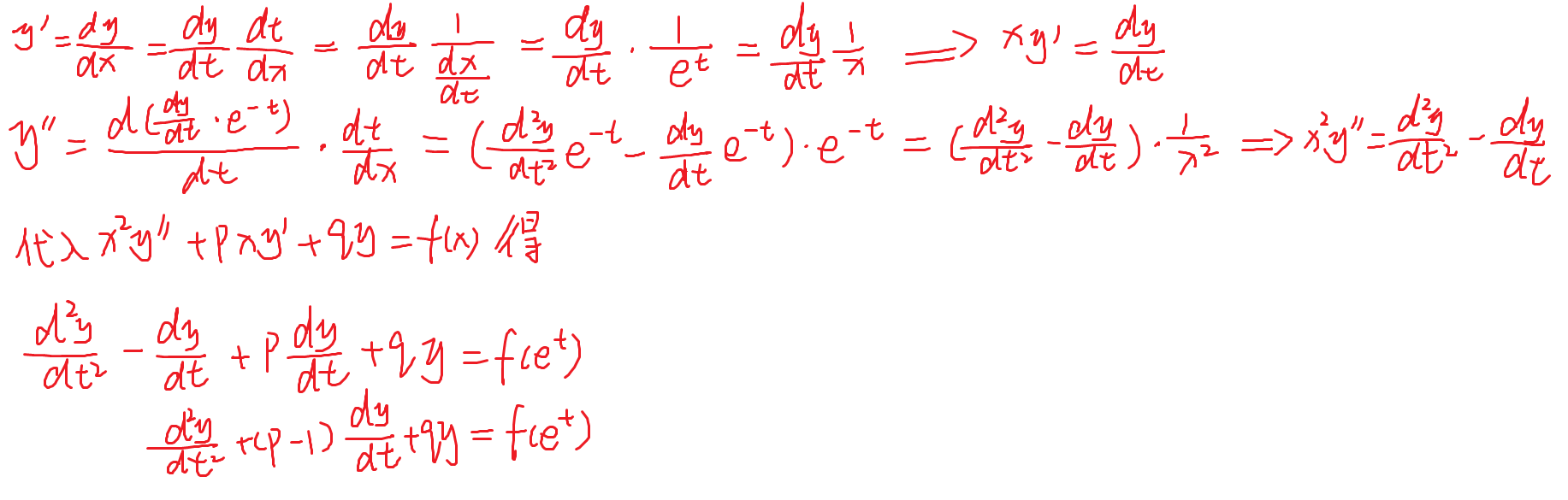
227-判断是否连续

补充题目

243-二阶导数定义

245-由条件求全微分

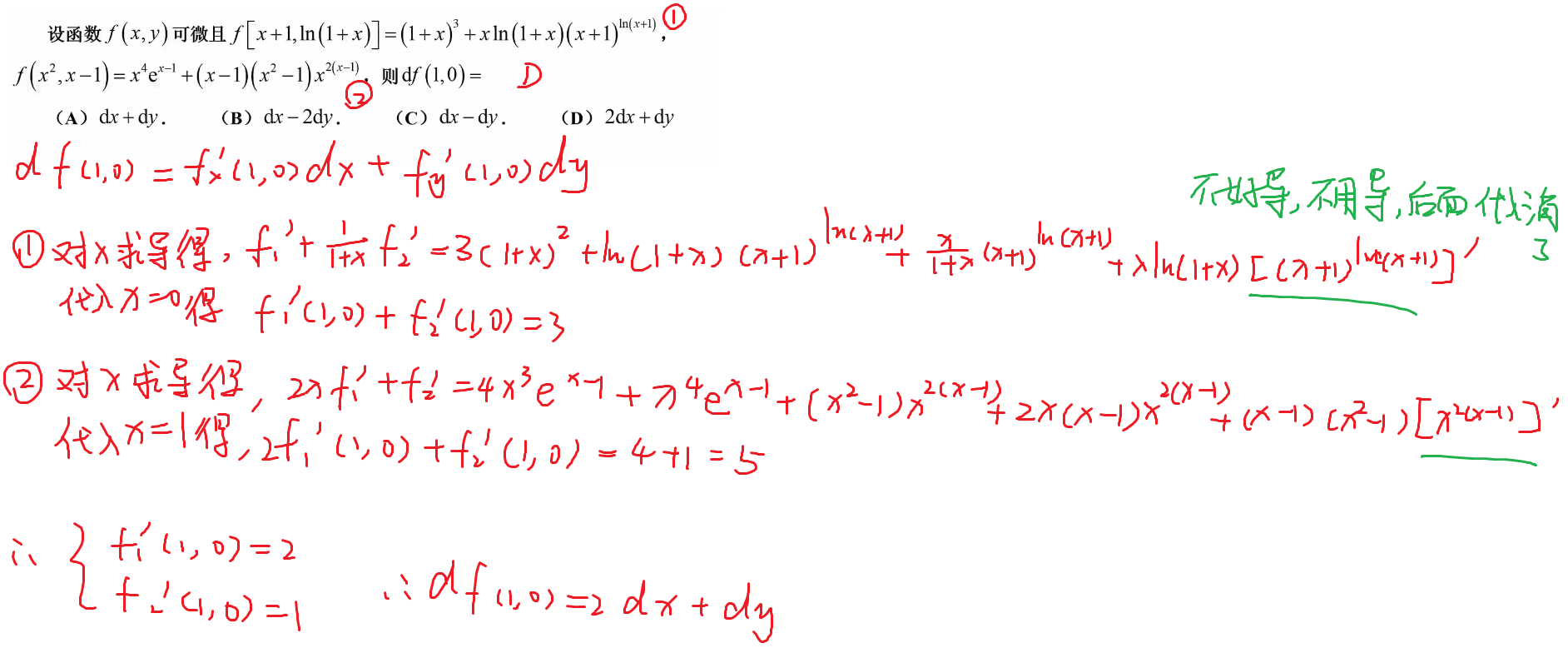
补充题目

248-多元函数判断极值点

249-隐函数存在定理

251-闭区域求最值

补充题目

660(多重积分)

106-直角交换积分次序

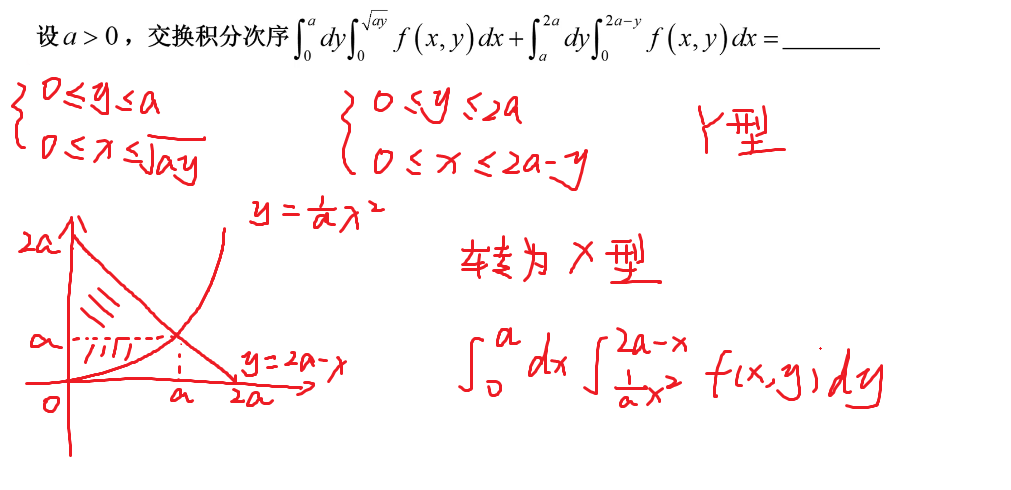
补充题目

109-极坐标交换积分次序

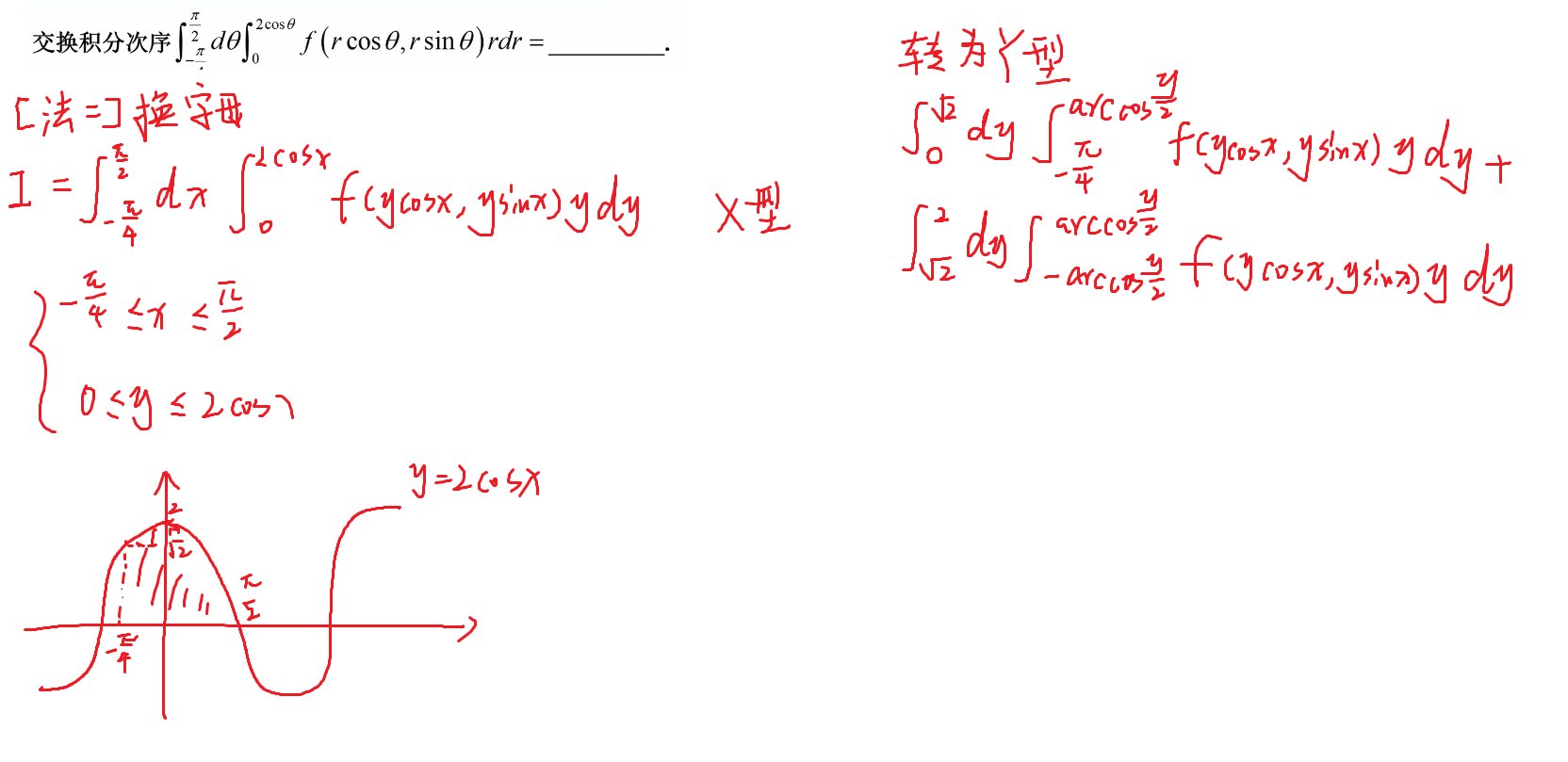
补充知识点

113-定积分定义

补充知识点

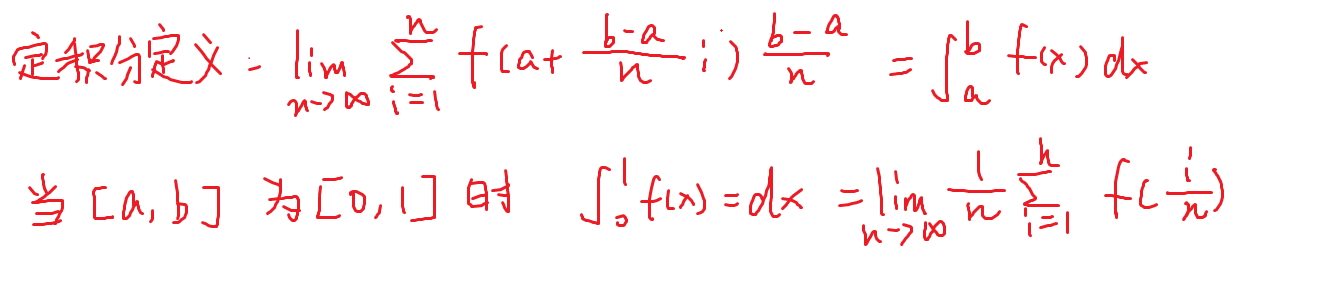
114-平移换元

115-轮换对称性

补充题目

116-偶倍奇零

262-平移坐标轴

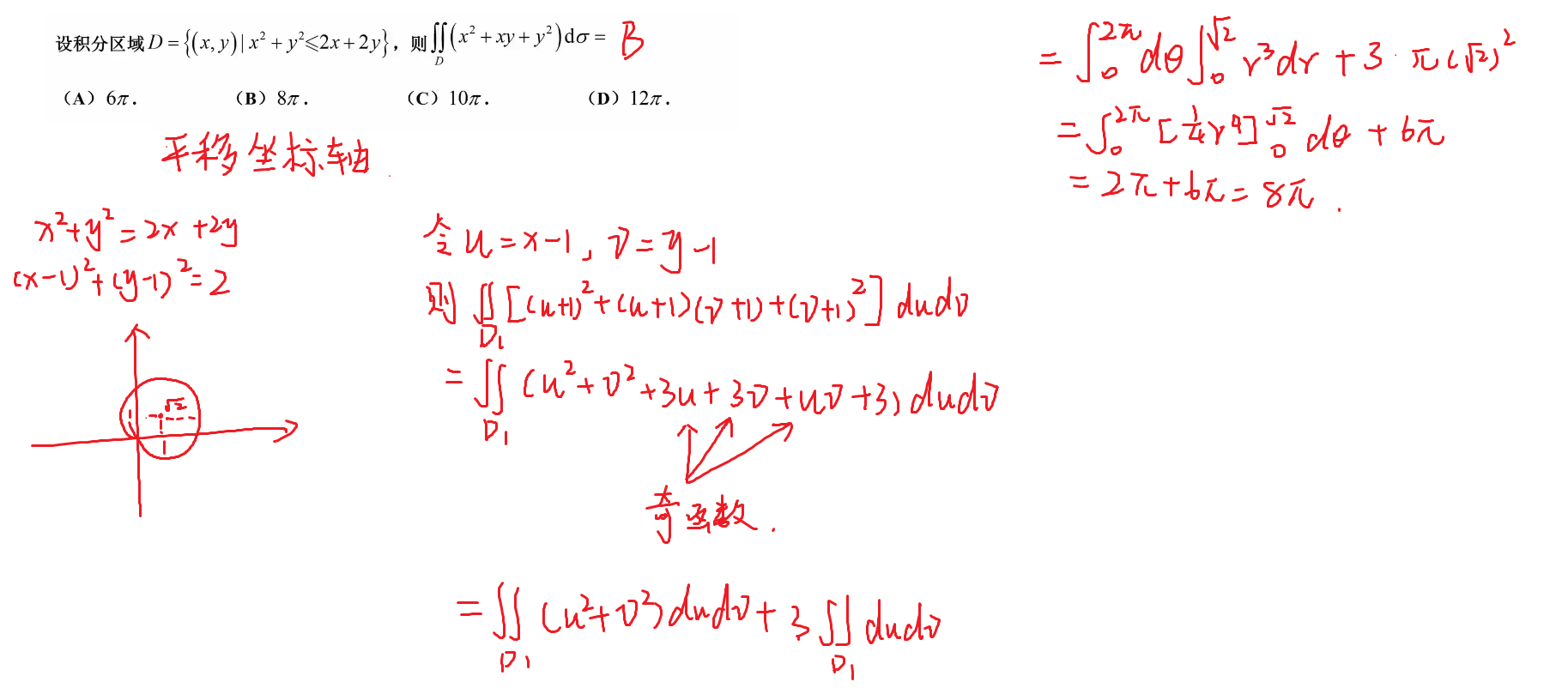
补充题目

269-区间在现

270-比较大小

272-轮换对称性

273-二重积分中值定理

补充题目

严选题

严选题（极限）

7-极限和点的关系

8-极限存在

补充题目

22-∞-∞型

23-1^∞型

32-0/0型

34-∞/∞型

35-1^∞型

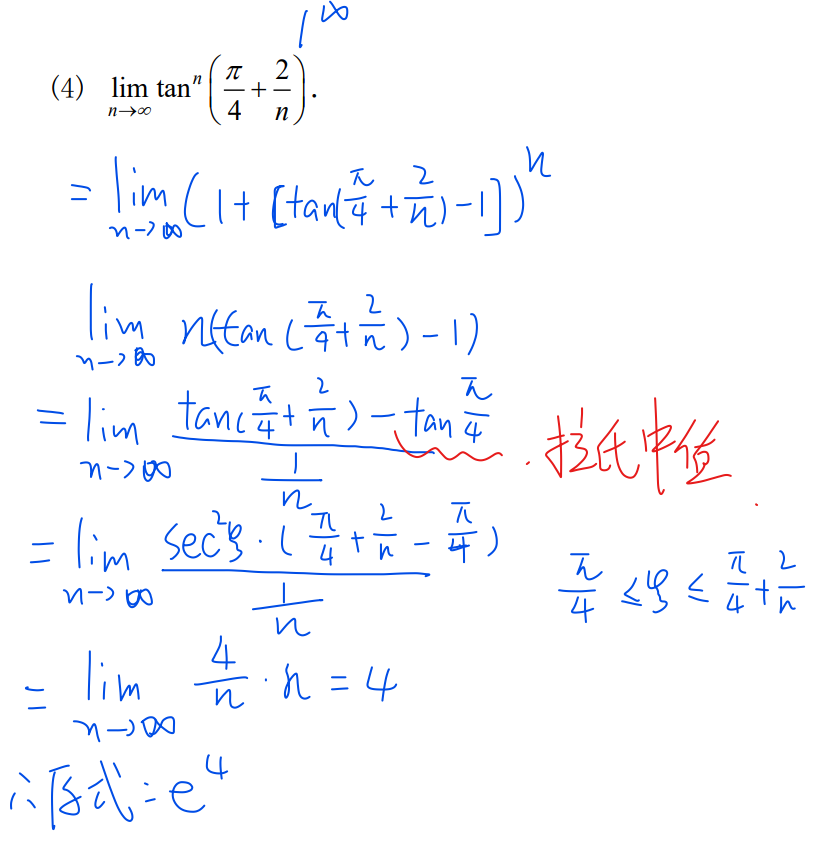
37-综合题

38-n项和的数列极限

40-数列夹逼和定积分共用

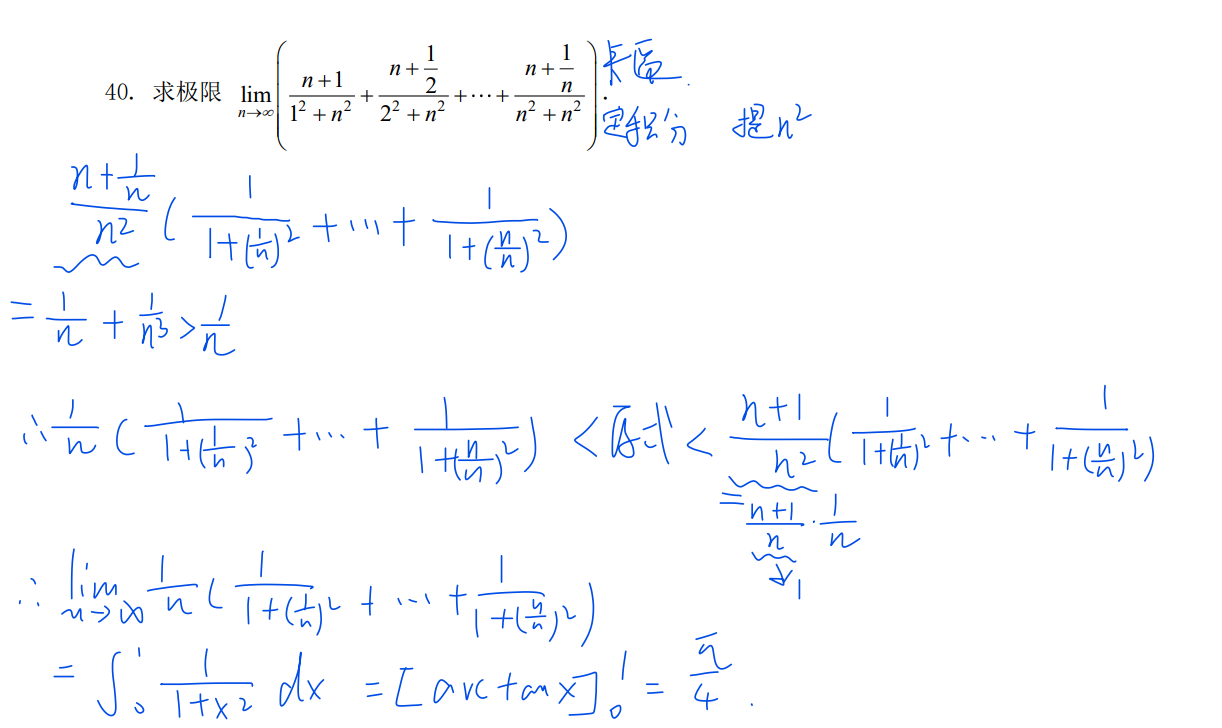
43-证明数列有极限

44-数列地推关系

13-无穷小量的最高阶

29-无穷小求未知数

严选题（导数）

1-可导的充分条件

2-导数存在但不连续的例子

7-找不可导点

8-找不可导点

29-换元

33-讨论导数连续性

16-求渐近线

26-罗尔定理求零点个数

35-二阶导判断极值点

36-二阶导判断参数方程性质

28-单调区间求根数量

37-通过一阶导判断根数量

39-分离参数求根数量

40-两函数交点求根数量

43-取对数证明不等式

严选题（积分）

14-凑分母

10-缩放夹逼

19-常见换元

21-积分的奇偶性

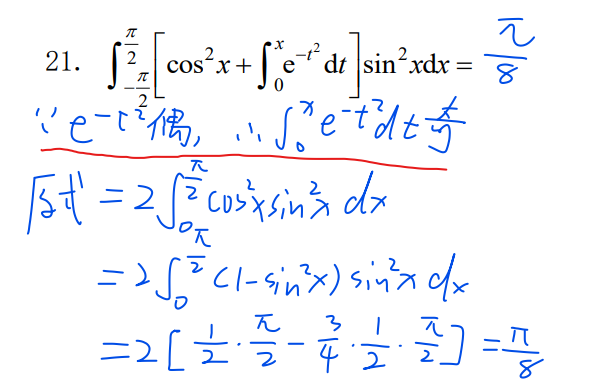
23-常见换元

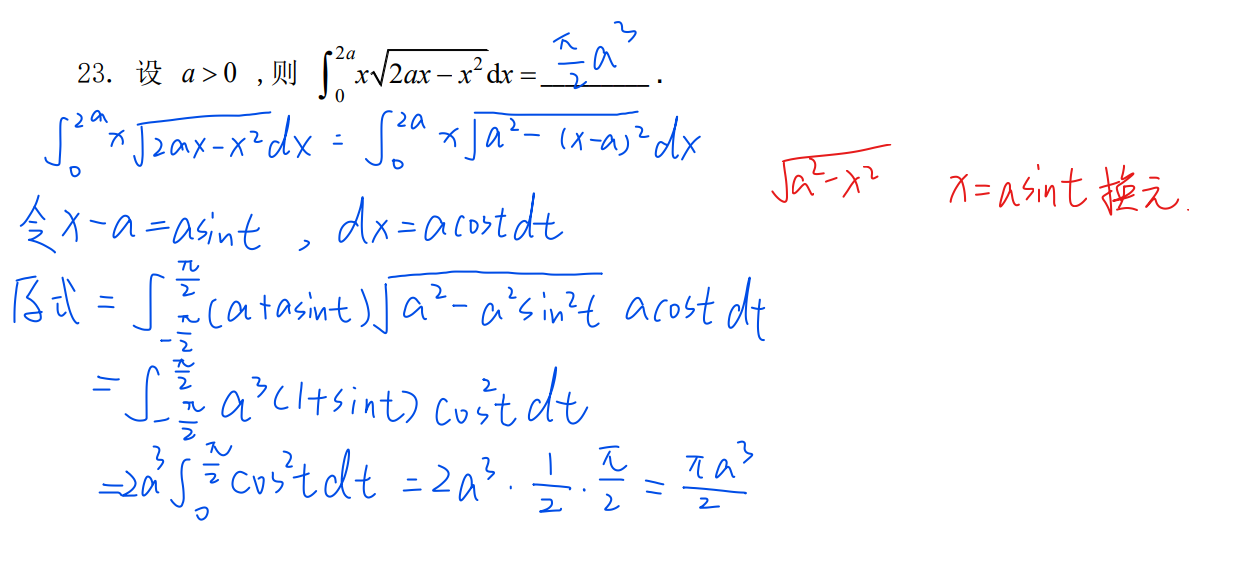
24-两端积分

28-积分求极限

44-缩放夹逼

30-变上限积分

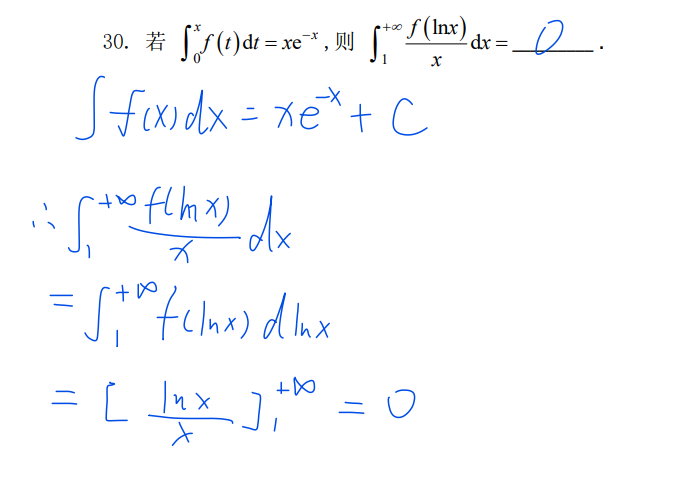
37-变上限积分

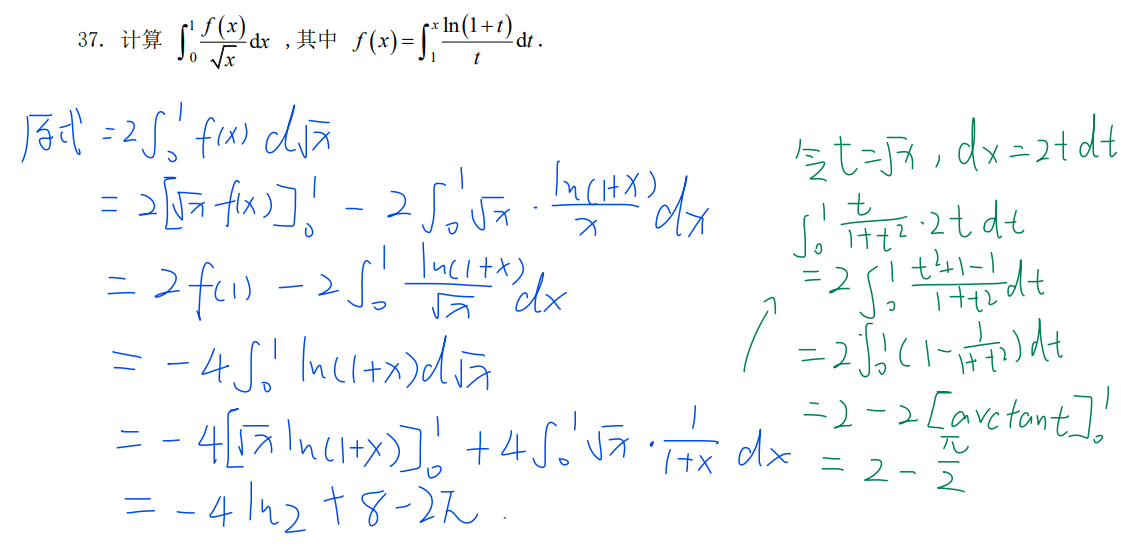
43-变上限夹逼缩放

46-罗尔定理

47-罗尔定理

48-找原函数 罗尔定理

49-找原函数 罗尔定理

50-积分中值定理

33-定积分应用 函数图像

55-做功

61-心形线

严选题（微分方程）

11-非齐次方程通解

14-非齐次方程通解

19/20-知特解求通解/颠倒x、y

强化例题（极限 导数）

强化例题（函数）

有界条件

f(x)在(a, b)连续，f(a)、f(b)有定义

导数和有界的关系

f’(x)在有限区间有界，f(x)也有界

导数和单调性的关系

一个点的导数值不能说明小区域内的单调性

而如果导数连续，则由保号性可知存在一个小区域是单调的

单调性

强化例题（极限性质）

极限性质

数列极限

数列敛散

数列极限性质

数列极限证明题

极限性质

强化例题（求极限方式）✨

等价无穷小代换

泰勒展开

补充

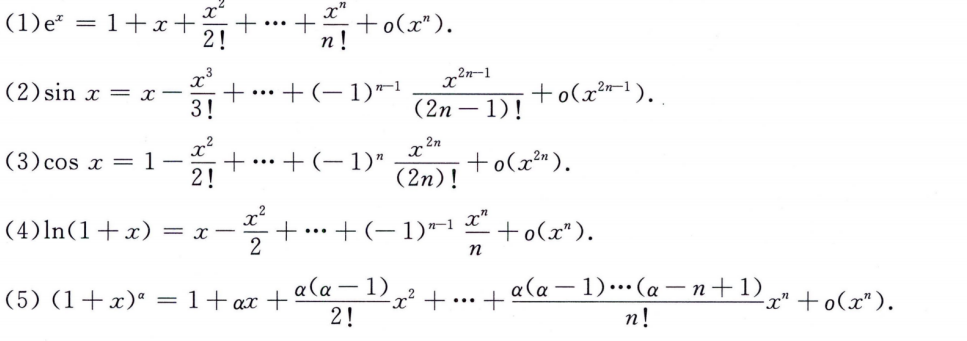
夹逼准则

定积分定义

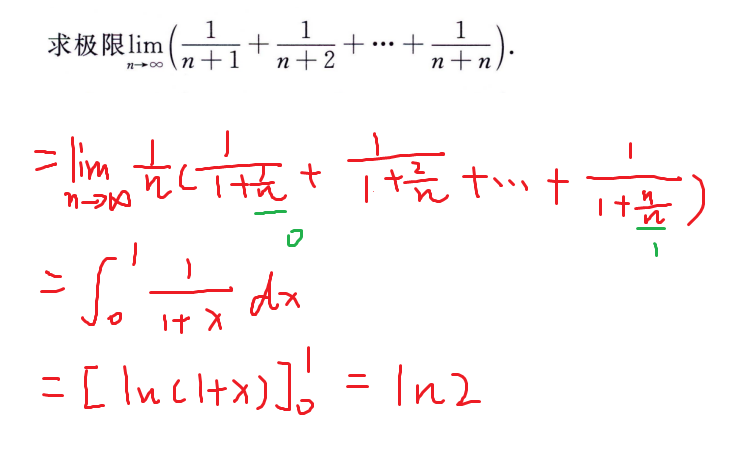
单调有界则有极限

强化例题（极限7种不定式）✨

0/0型

常用方法：

1. 洛必达
2. 等价无穷小代换
3. 泰勒公式

化简常用方法：

1. 非零因子带入
2. 有理化
3. 变量代换

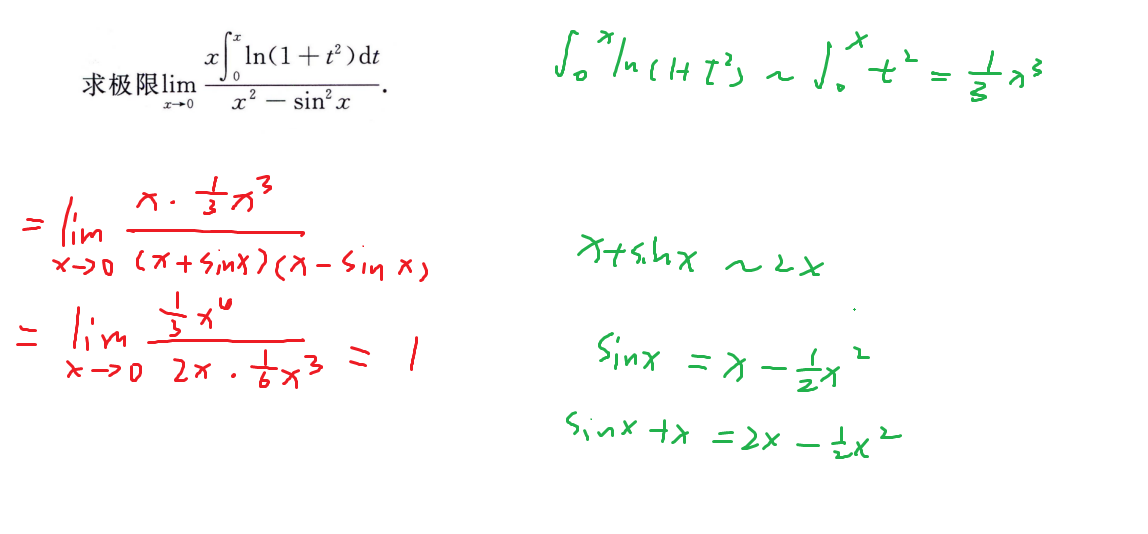
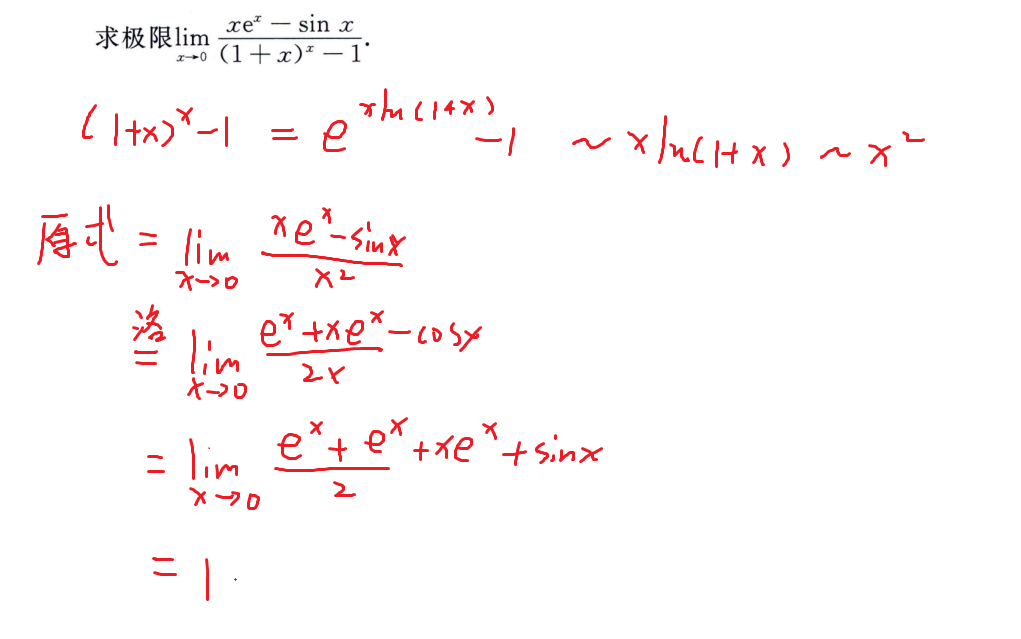
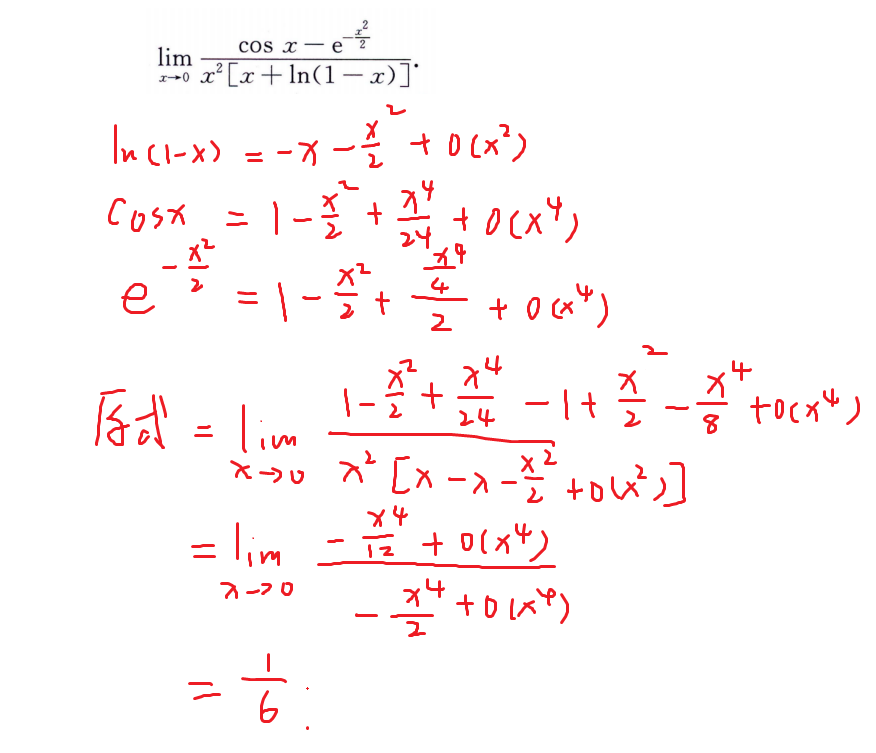
∞/∞型

常用方法：

1. 洛必达
2. 分子分母同除以分子和分母各项中最高阶的无穷大

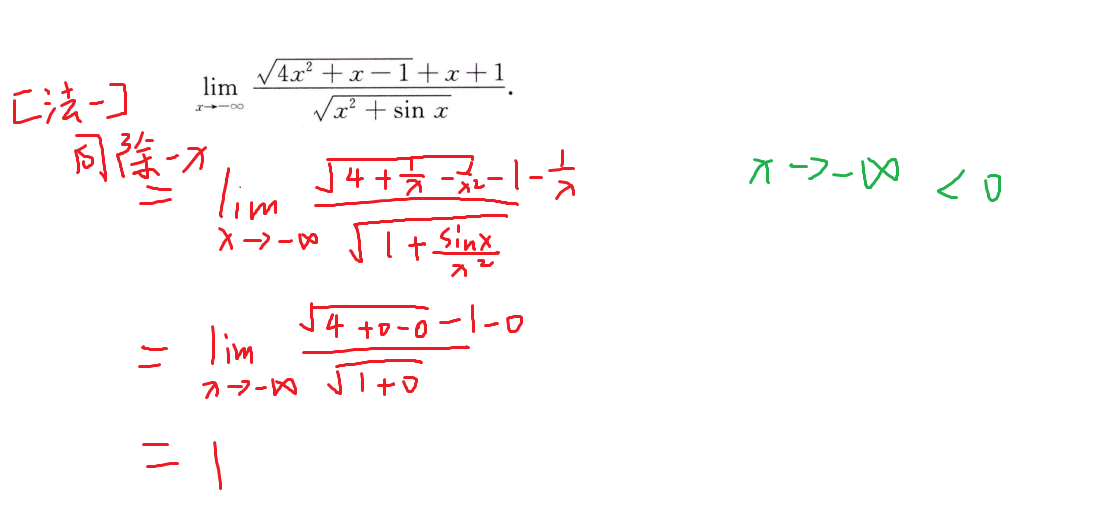
∞ - ∞型

常用方法

1. 分式差：通分为0/0
2. 根式差：根式有理化
3. 提无穷因子，然后等价代换或变量代换、泰勒公式

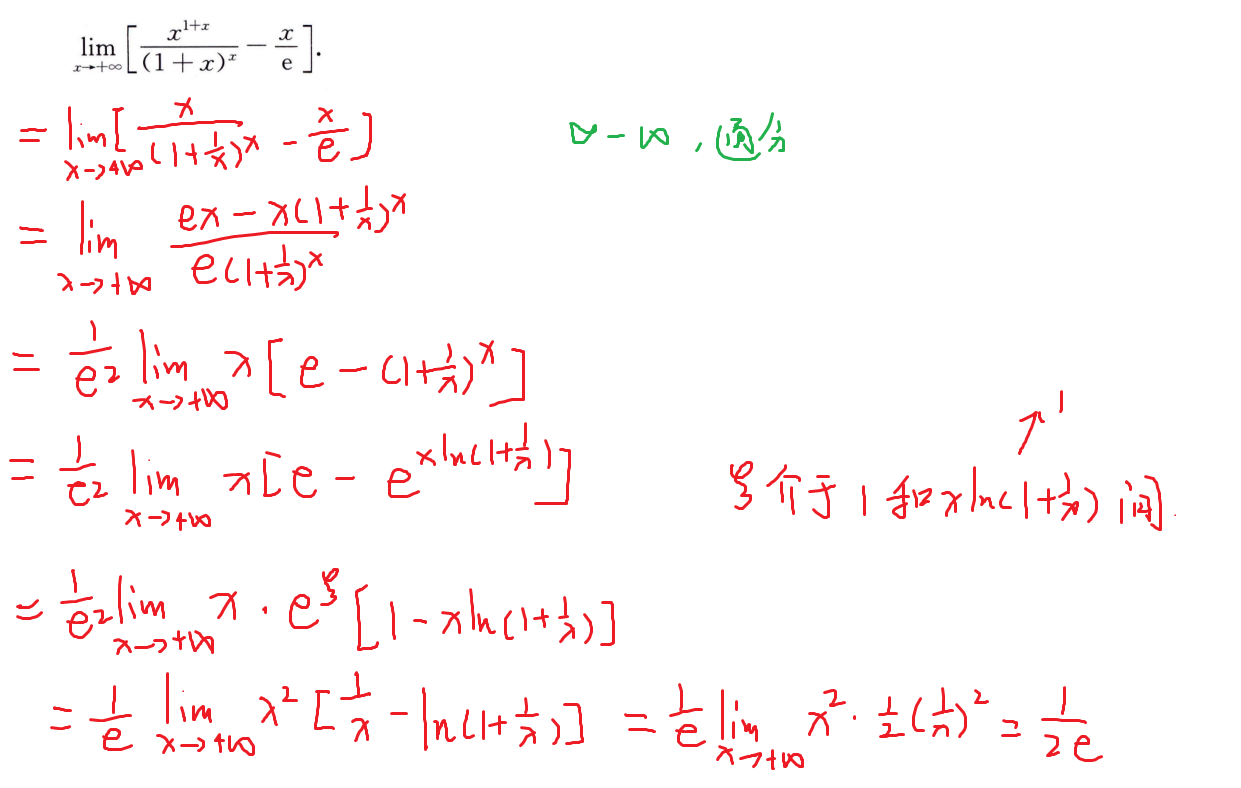
0 * ∞型

常用方法

1. 化为0/0或∞/∞

1^∞型

常用方法

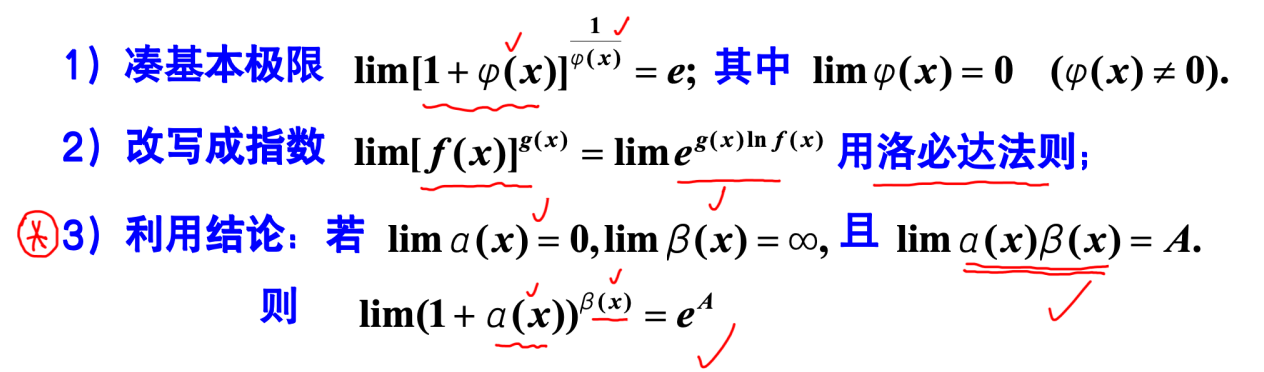
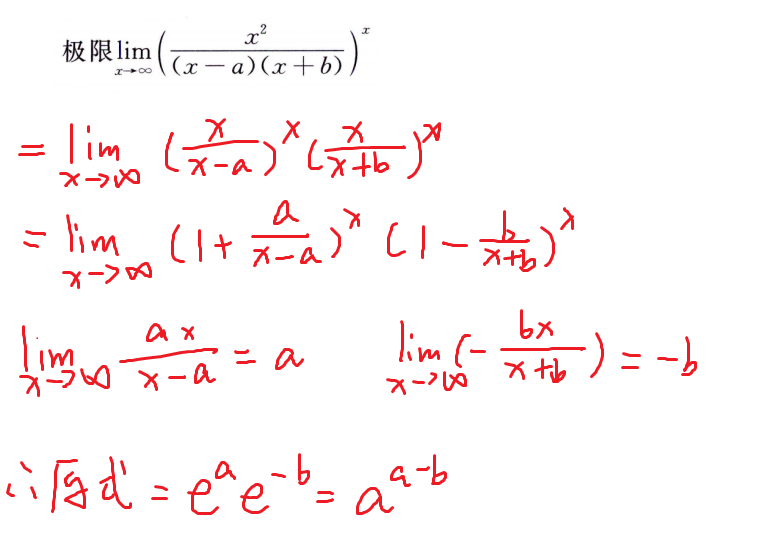
0^0型和∞^0型

常用方法

1. 取对数

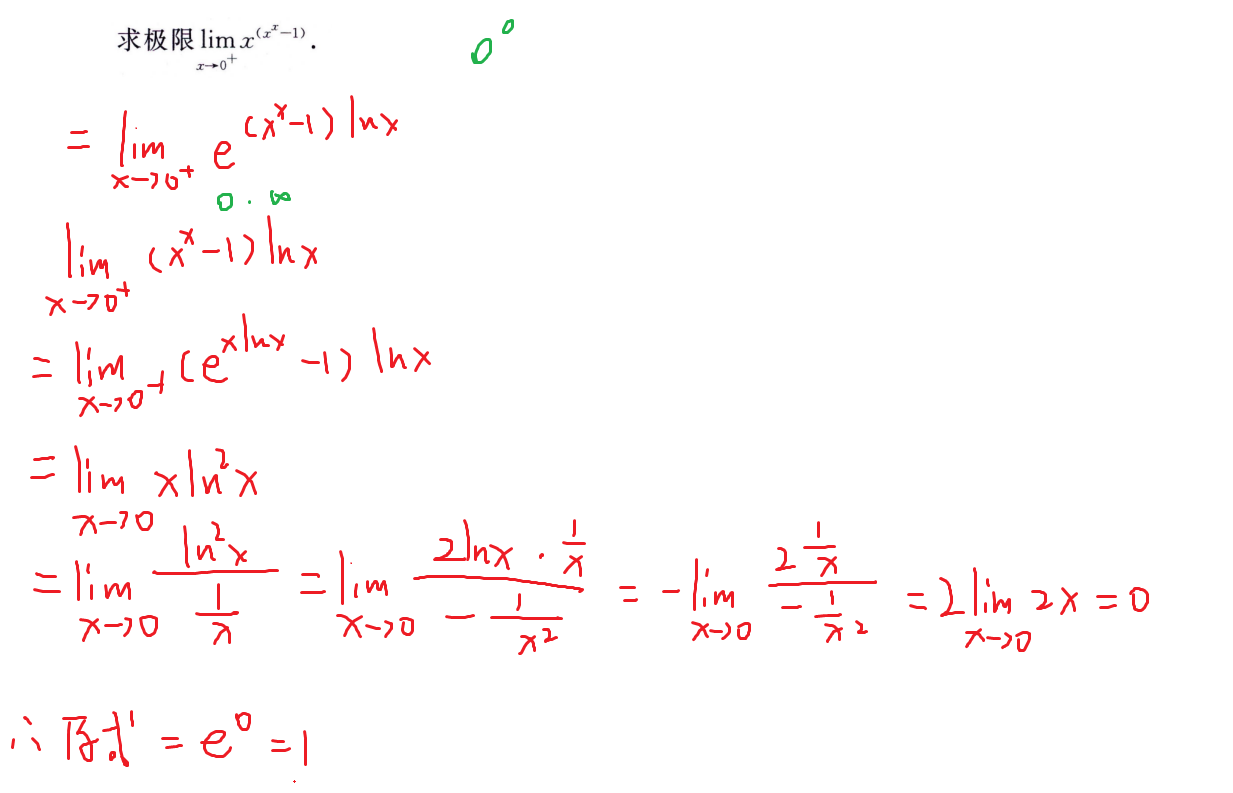
确认极限中参数

强化例题（数列极限）

不定式

n项和的数列极限

常用方法

1. 夹逼原理（变化部分是主体的次量级）
2. 定积分定义（变化部分是主体的同量级）
3. 级数求和

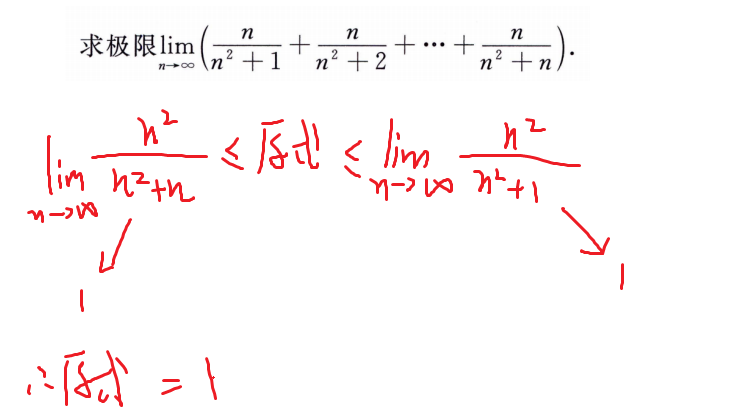
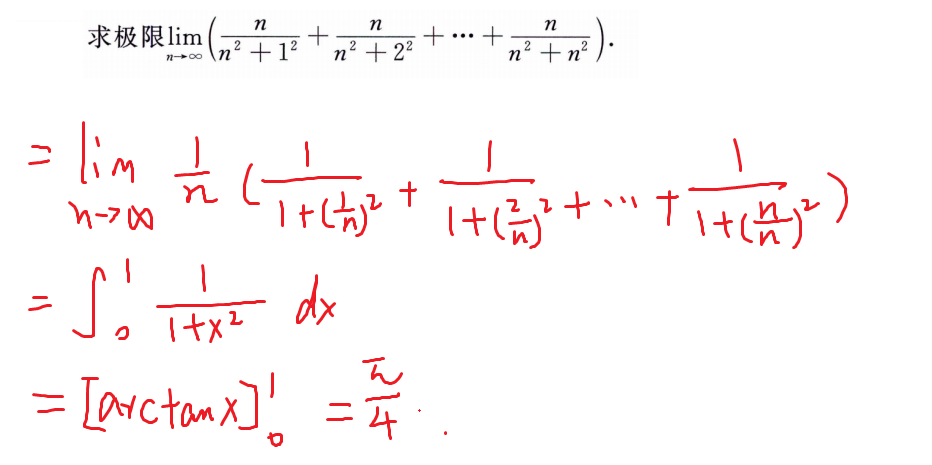
n项乘的数列极限

常用方法

1. 夹逼定理
2. 取对数化为和的形式

递推关系（难点）

常用方法

1. 证数列收敛（单调有界），然后求极限
2. 先令极限为A，然后等式两端取极限解得A，最后证明极限为A

单调性判定常用方法

1. Xn+1 - Xn

2. 同号时，Xn+1 / Xn

3. X1 = a，Xn+1 = f(Xn)

   f(x)单调增，则x1<=x2时，数列单调增

   f(x)单调增，则x1>=x2时，数列单调减

4. f(x)单调减，数列不单调

强化例题（无穷小量的比较）

比较两个无穷小的常用方法

1. 洛必达
2. 等价无穷小代换
3. 泰勒公式

强化例题（连续）

概念

连续：极限值等于这个点函数的值

左（右）连续：左（右）极限等于函数值

定理：f(x)连续 <==> f(x)左连续且右连续

间断点：f(x)在x0某去心邻域有定义，但在x0处不连续，则x0为间断点

间断点分类：

1. 第一类间断点：左右极限均存在

   可去间断点：左右极限相等

   跳跃间断点：左右极限不等

2. 第二类间断点：左右极限至少有一个不存在

   无穷间断点

   振荡间断点

零点定理：f(x)在[a, bn]上连续，且f(a)f(b)<0，则存在一点∈(a, b)使f=0

讨论连续性及间断点类型

介值定理、最值定理和零点定理的证明题

强化例题（导数）

概念

导数：

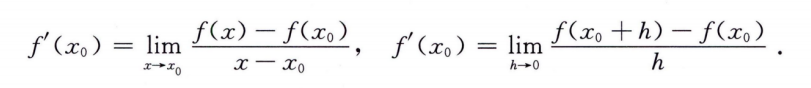
可导 <==> 左右导数存在且相等

微分：

几何意义：

1. 导数：切线斜率
2. 微分：切线上的增量

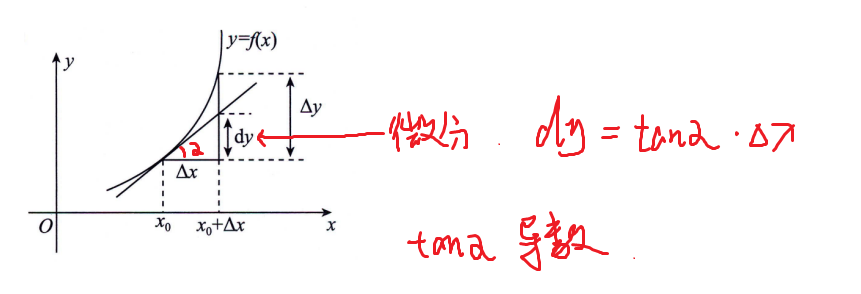
f(x)n阶可导 ==> 洛必达能用到n-1次导数

f(x)n阶连续且可导 ==> 洛必达能用到n次导数

导数定义求极限

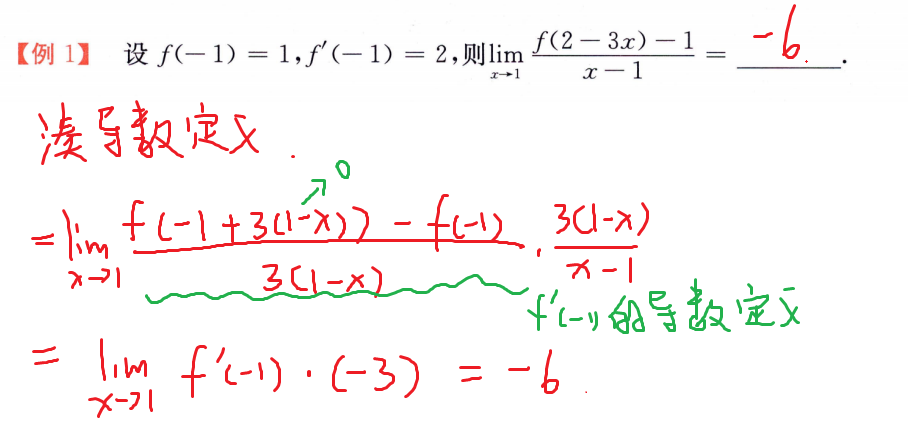
导数定义求导数

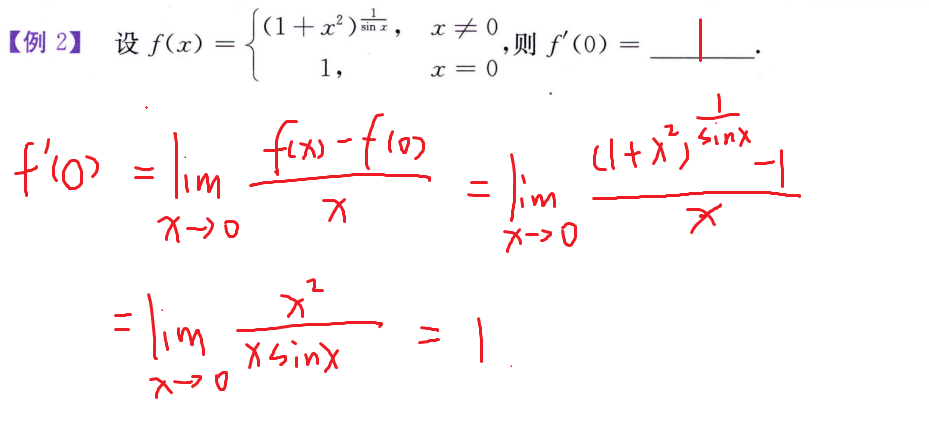
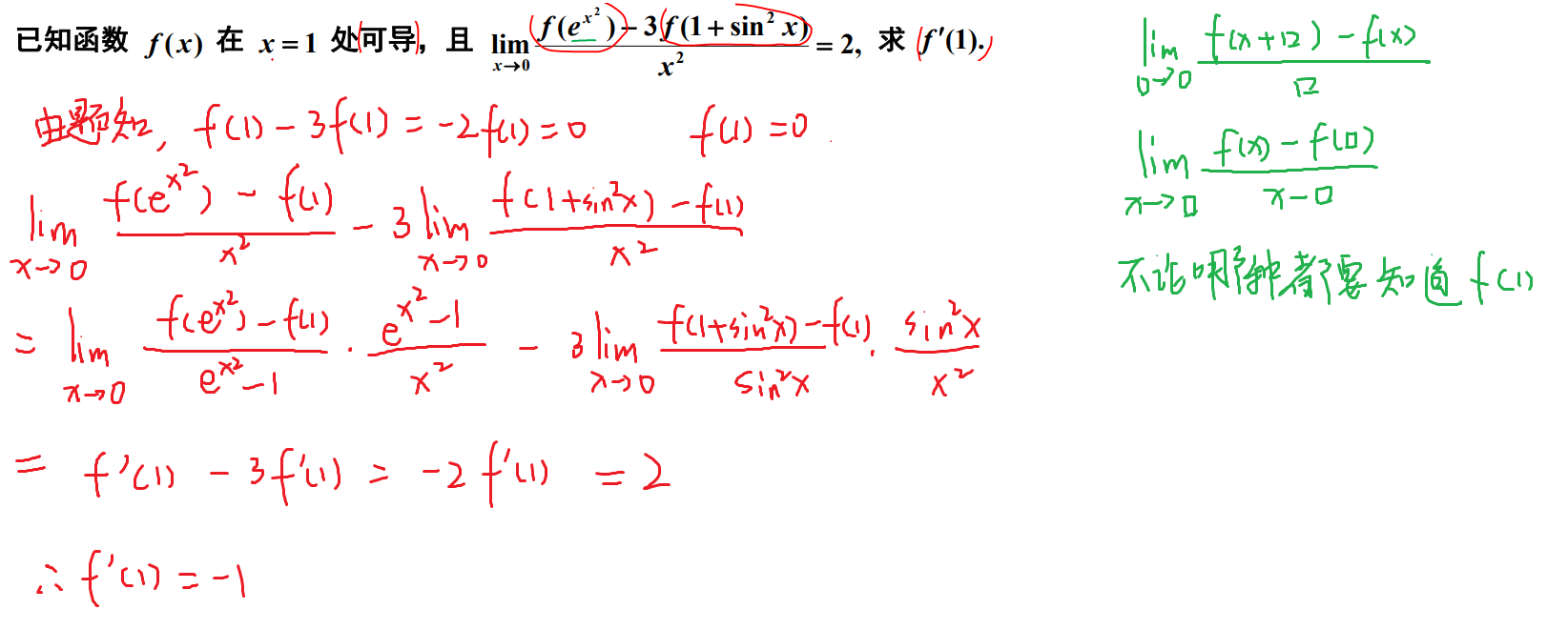
导数定义判断可导性✨

导数几何意义

重点在求dy/dx

求导计算✨

复合函数求导

重点在链式求导

隐函数求导

重点在左右分别求导

参数方程求导

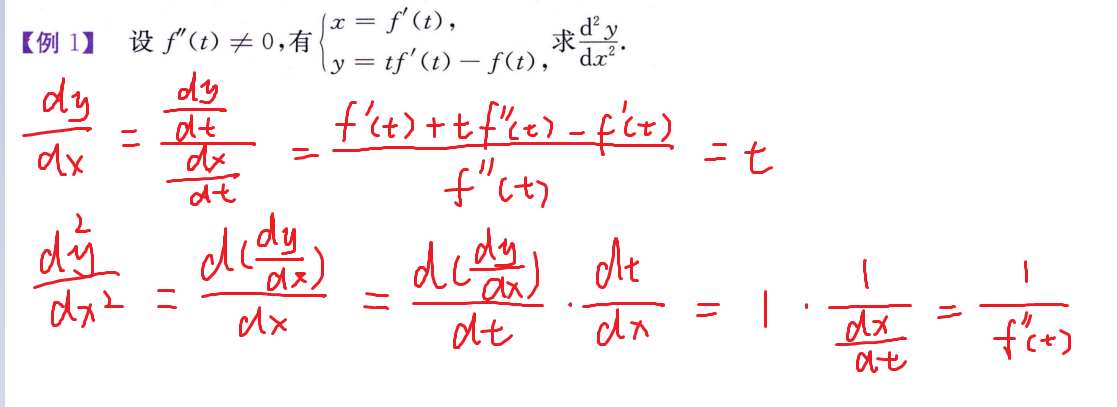
反函数求导

函数和反函数的导数互为倒数

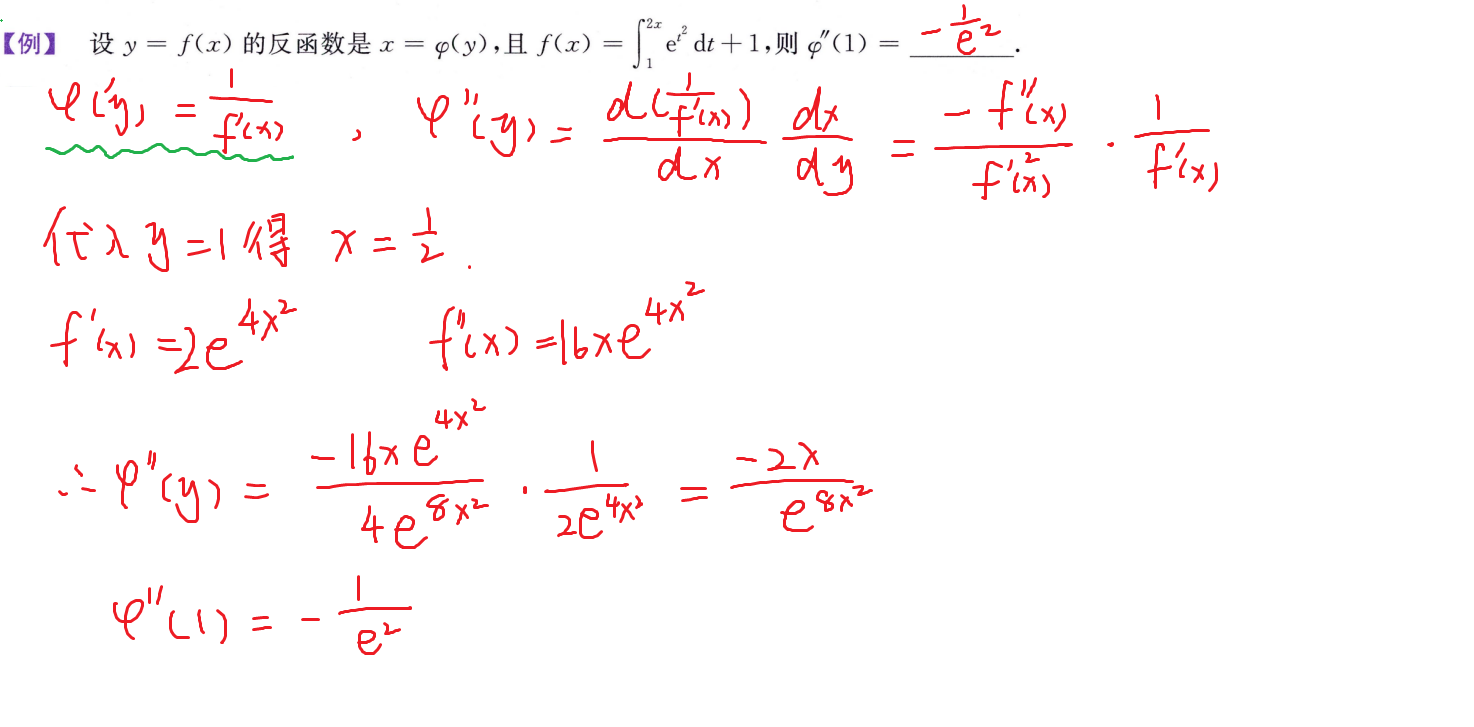
对数求导

适用于幂指函数，连乘，连除，开方，乘方

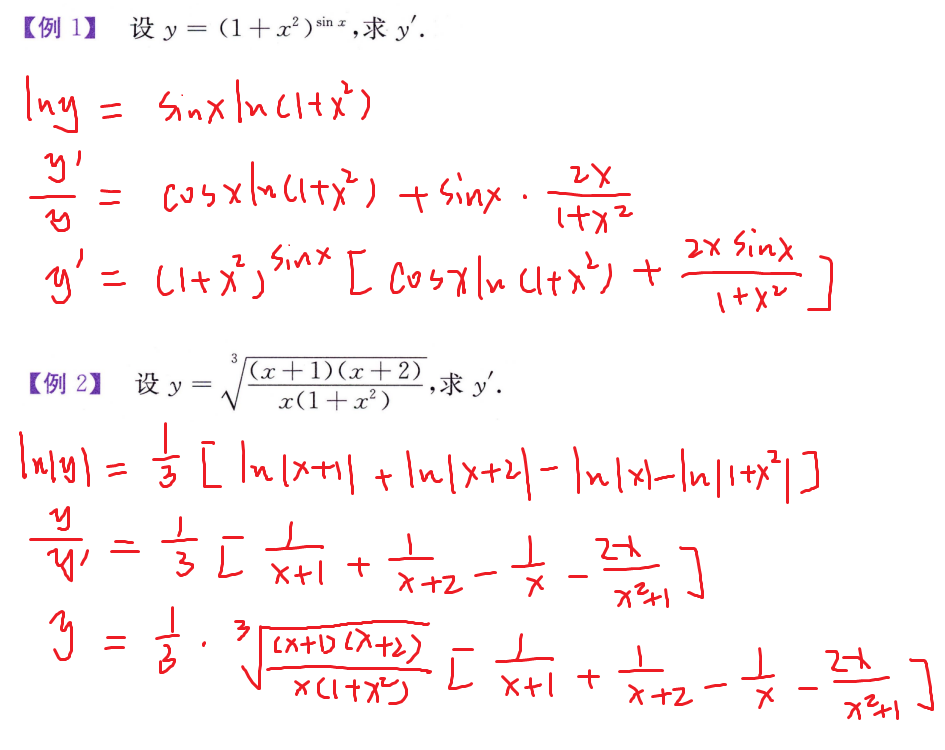
高阶导数

常用方法

1. 归纳
2. 泰勒公式

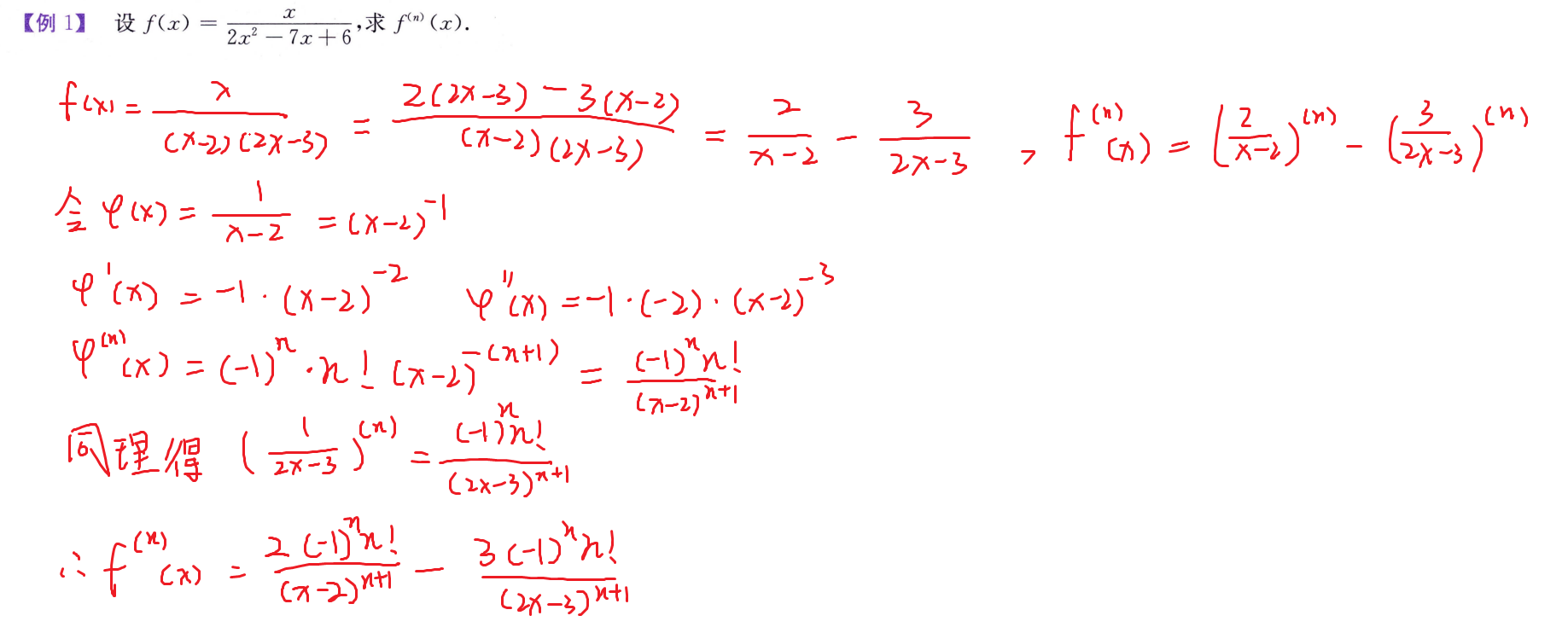
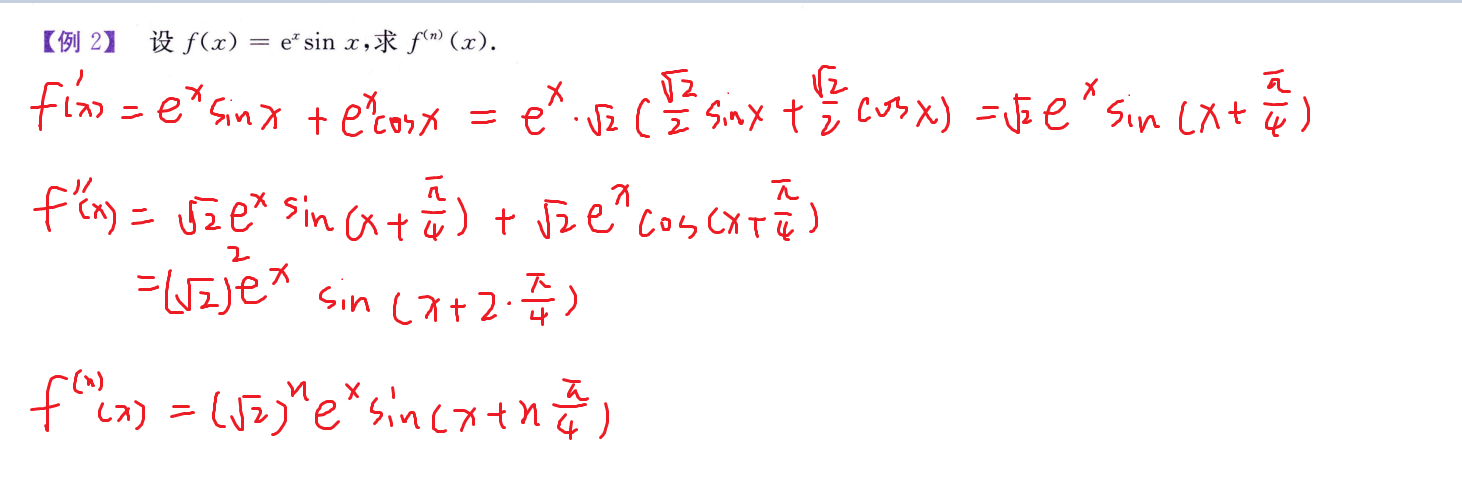
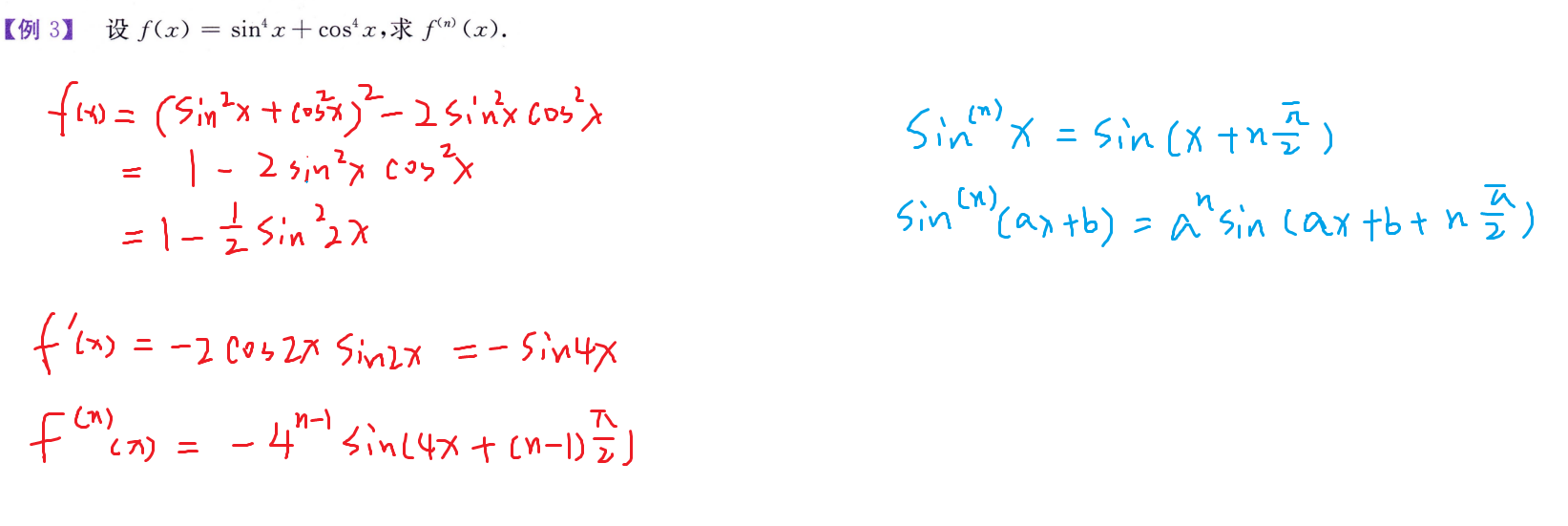
强化例题（导数应用）

概念

四个微分中值定理：

找极值：在驻点和不可导点上找

找最值：在驻点、不可导点和端点上找

极值的充分条件：

找凹凸区间：二阶导 > 0，凹；二阶导 < 0，凸；

找拐点：凹凸性相反的点（x0, f(x0)）

判断点左右两边二阶导的正负，

不好判断则看三阶导是否等于0

或判断第一个不为0的高阶导，奇为拐点

渐近线：

曲率：

函数单调性、极值、最值

凹点、拐点、渐近线及曲率

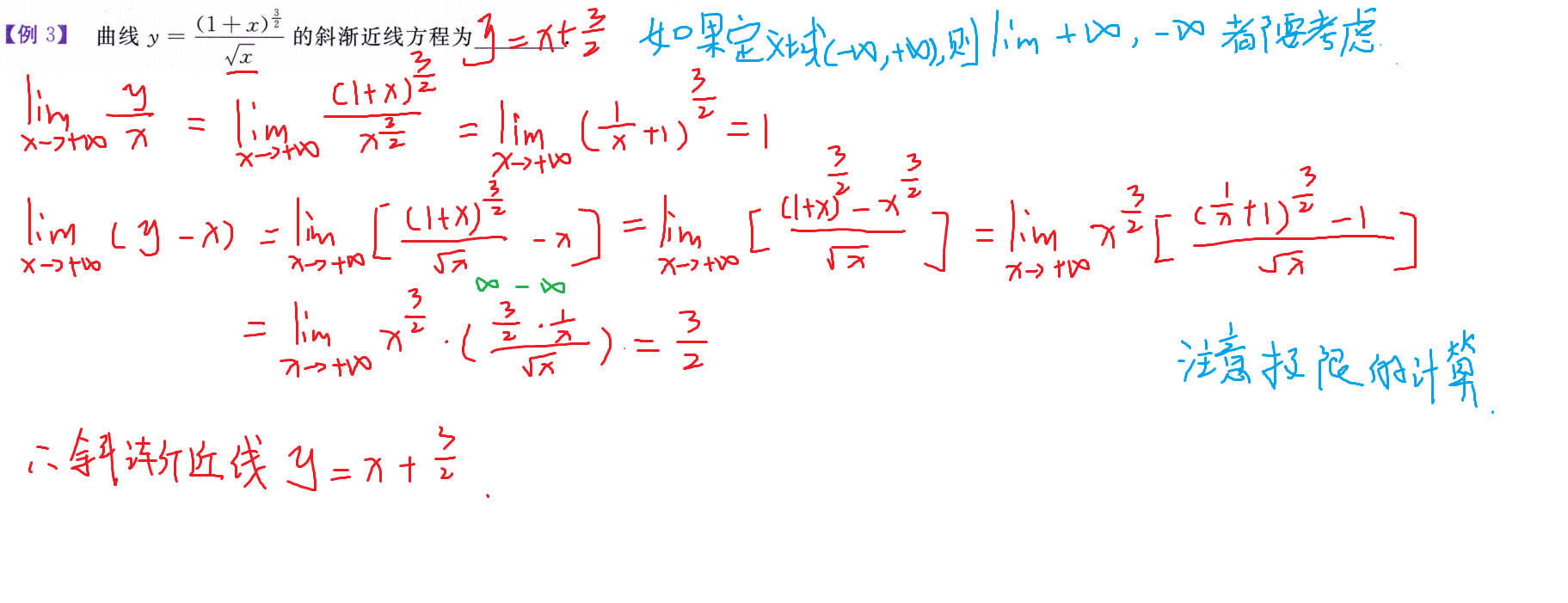
方程根的数量

罗尔定理推论：n阶导不等于0，则f(x) = 0最多有n个实根

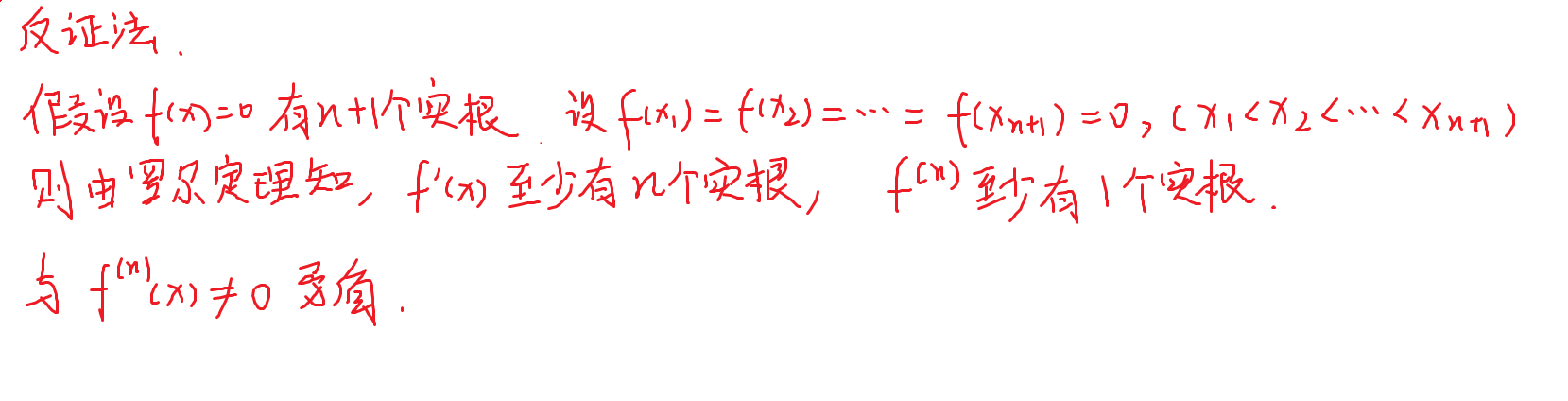
证明不等式

常用方法

1. 单调性
2. 最大最小值
3. 拉格朗日中值定理
4. 泰勒公式
5. 凹凸性

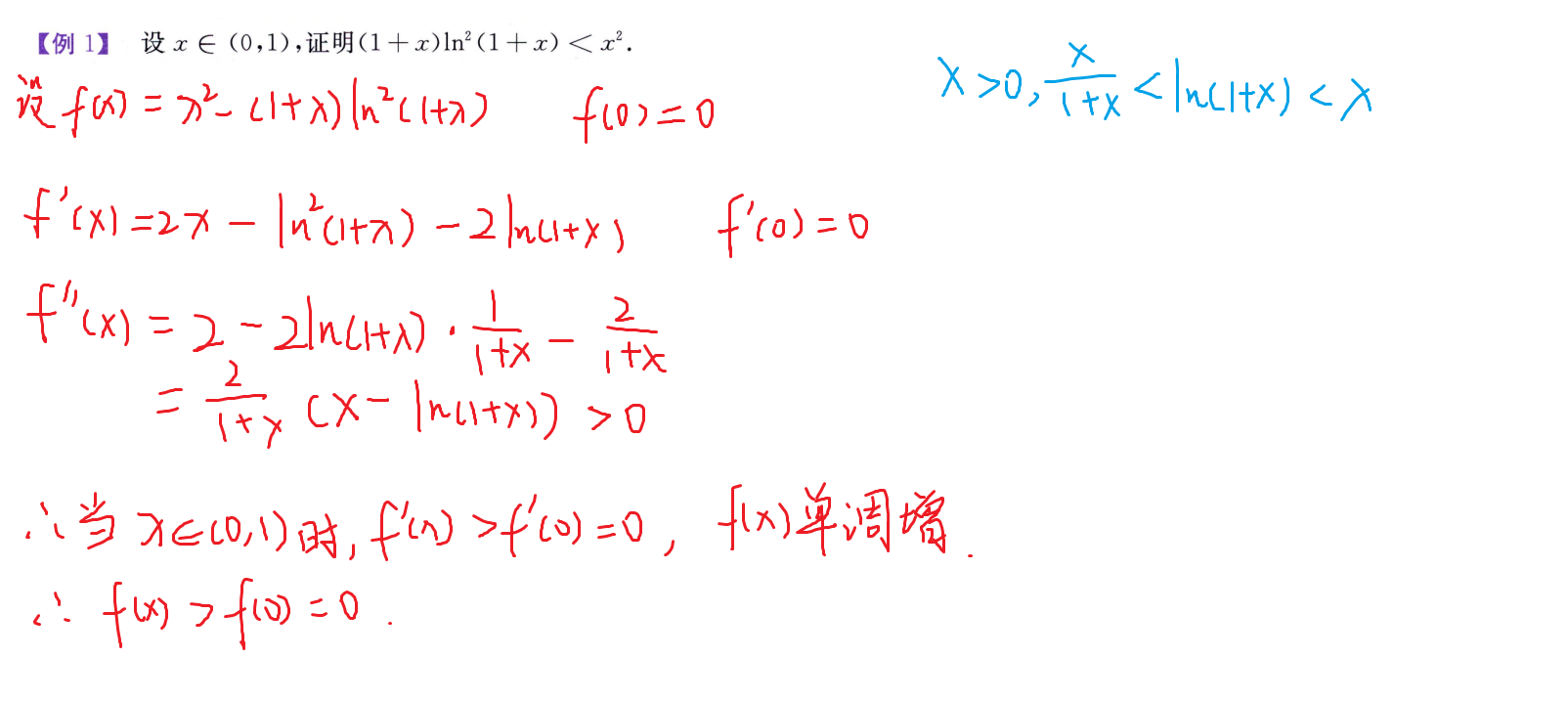
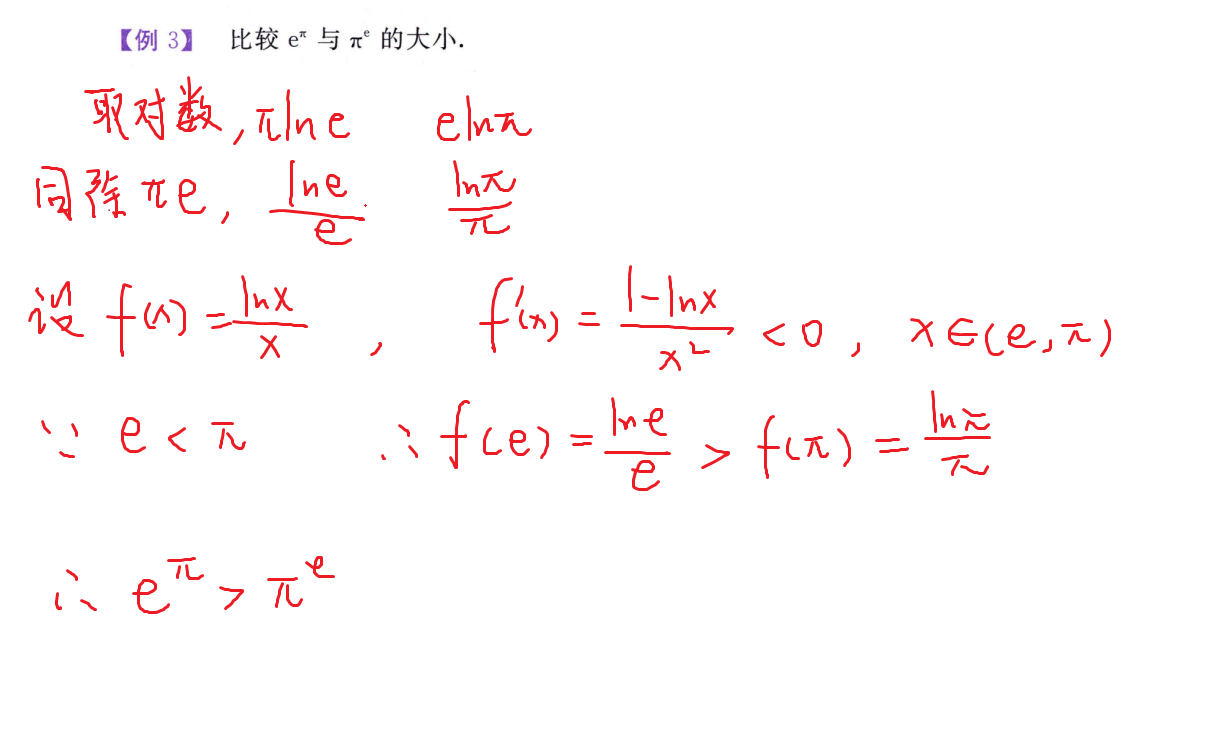
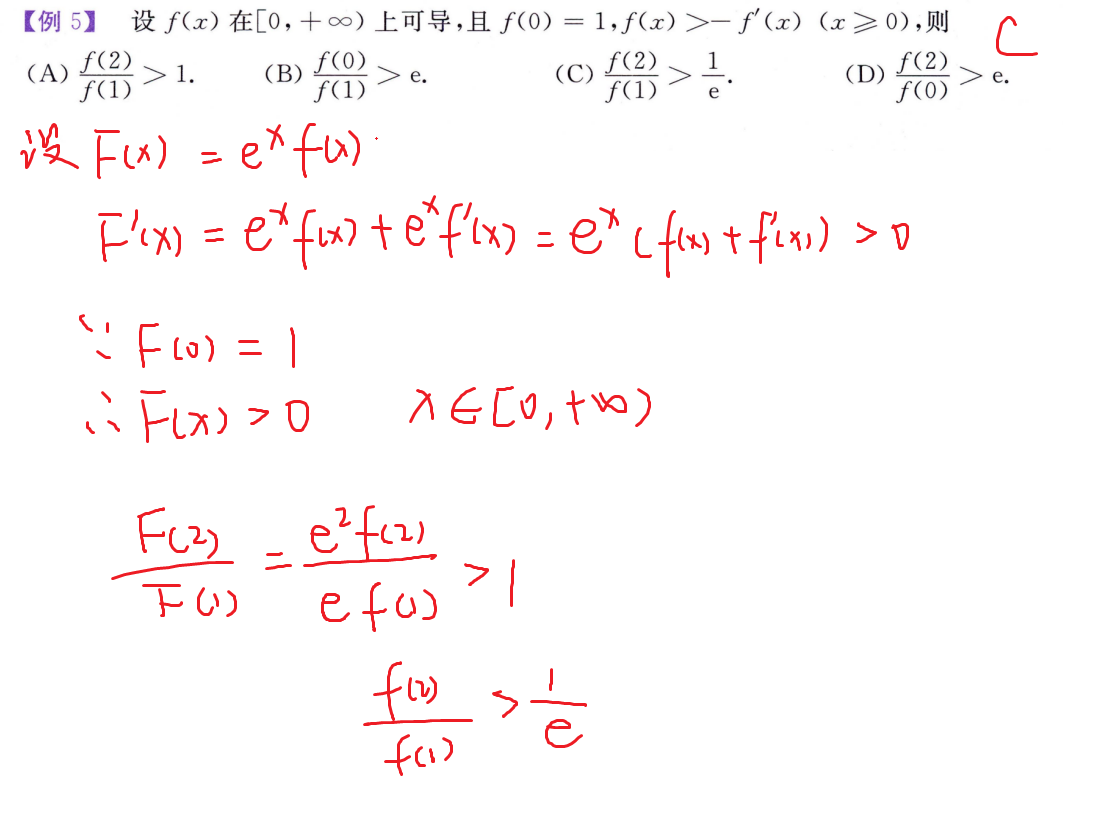
强化例题（微分中值定理证明题）✨

证明存在一点使得F(x, f(x), f’(x)) = 0

构造辅助函数常用方法

1. 分析法：分析找出原方程
2. 微分方程法：求出通解H(x, y) = C，设辅助函数g(x) = H(x, f(x))
3. 

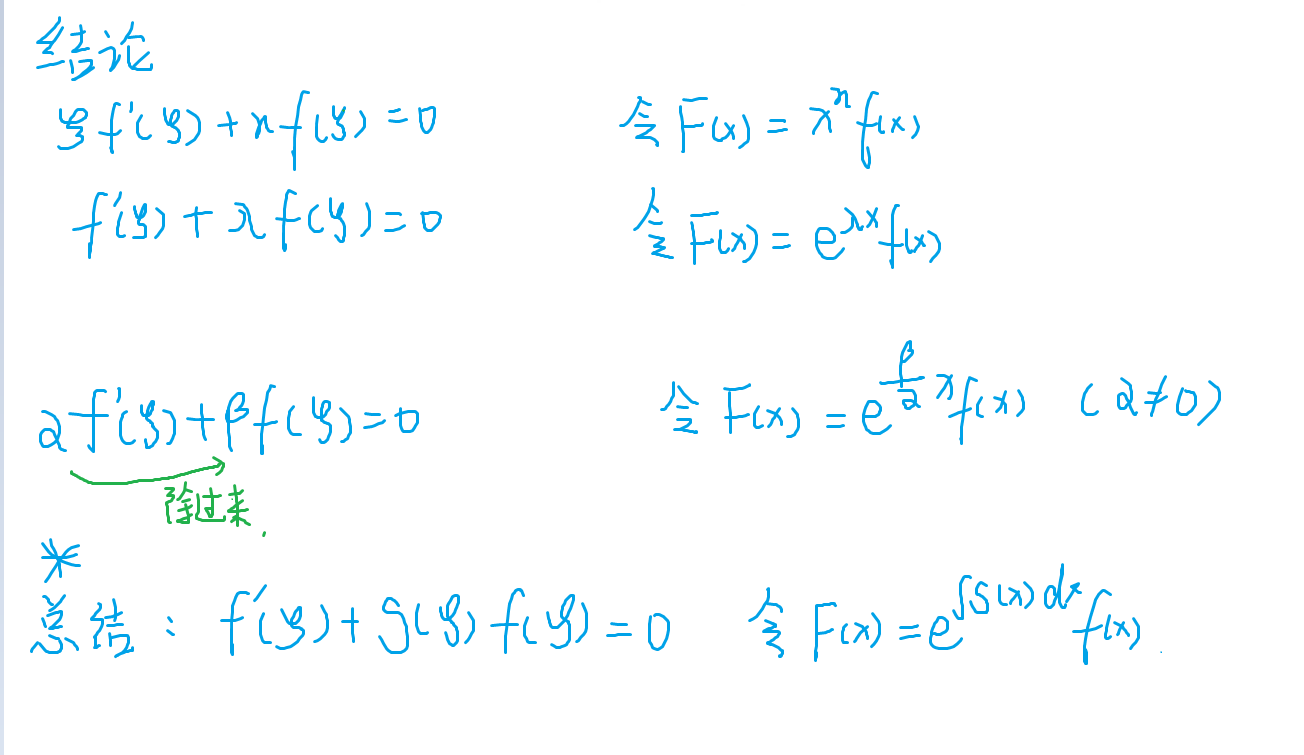
构造辅助函数的过程不用写

证明存在两点使得F(x, y, f(x), f’(x), f(y), f’(y)) = 0

注意双中值类型是两个未知数都在导数里

常用方法：

1. 没说x ≠ y的情况

   用两次中值定理（拉氏、柯西）

2. 说了x ≠ y的情况

   分为两个子区间，分别用拉氏中值定理

   定两个子区间时一般用到逆推法

证明存在一个点使F(x, f^n(x)) >= 0 (n>=2)

（难点，比较玄学）

常用方法

1. 用带拉格朗日余项的泰勒公式，在题目中提供信息多的点展开

强化例题（积分）

强化例题（不定积分）

概念

原函数存在性：

1. f(x)在区间I上连续，则在区间I上必有原函数
2. 在区间I上有第一类间断点（可取、跳跃），则在区间I上没有原函数

基本积分公式：

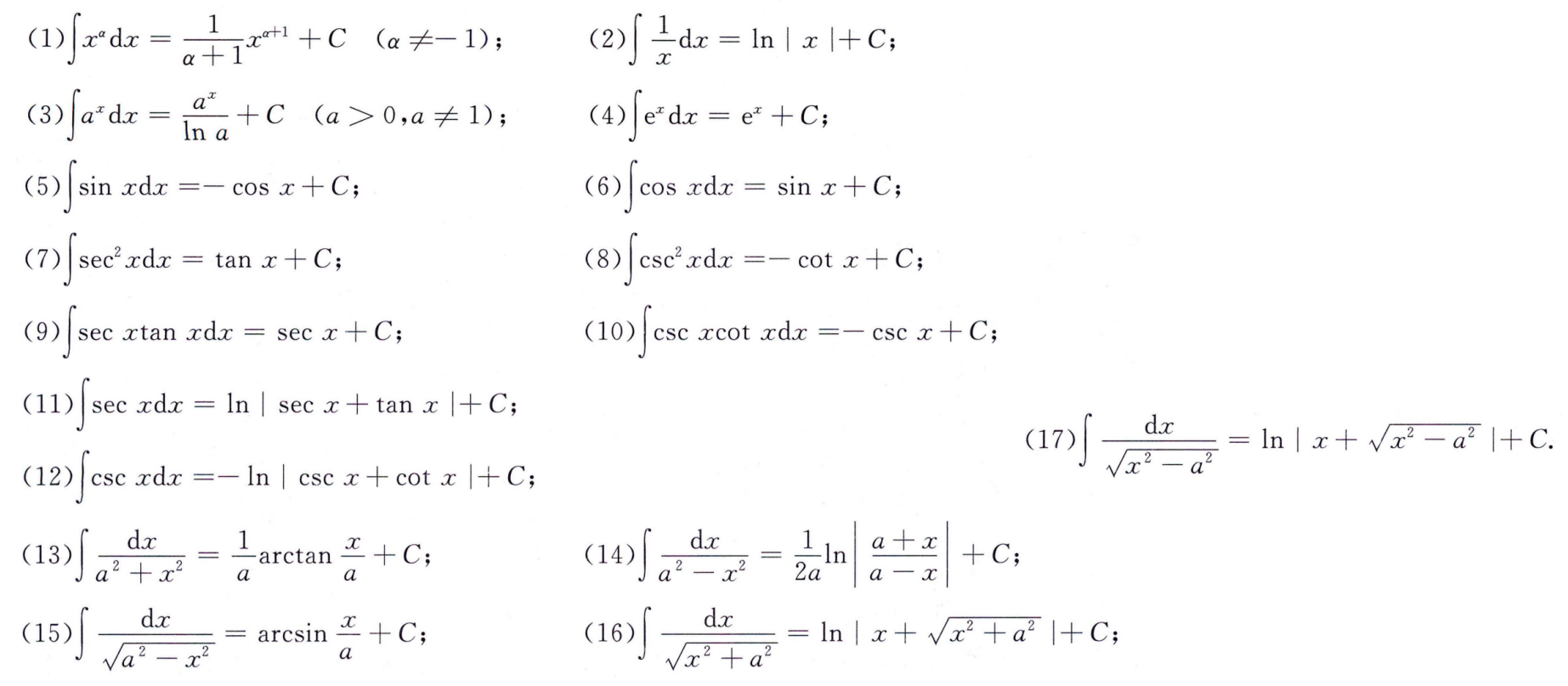
三种主要积分法：

三类常见可积函数积分：

不定积分例题

例题比较杂，不好分类

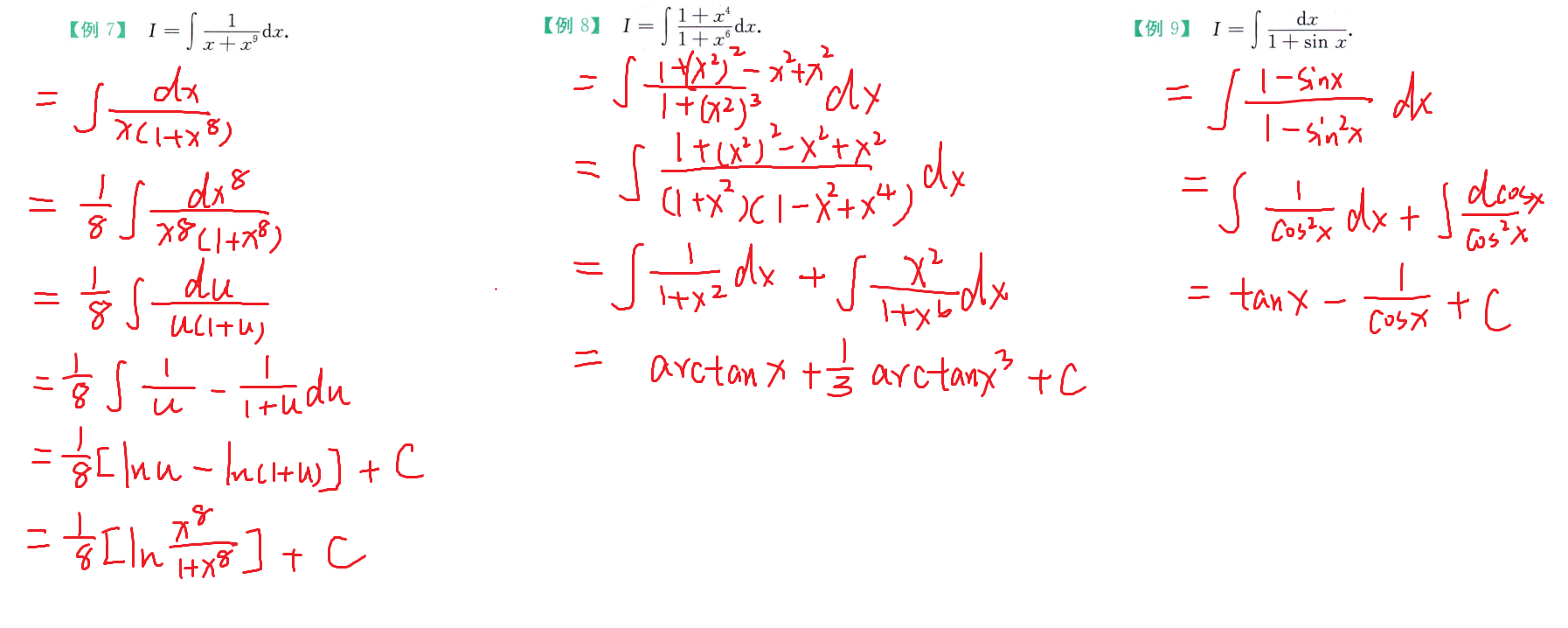
强化例题（定积分）

定积分性质

例题

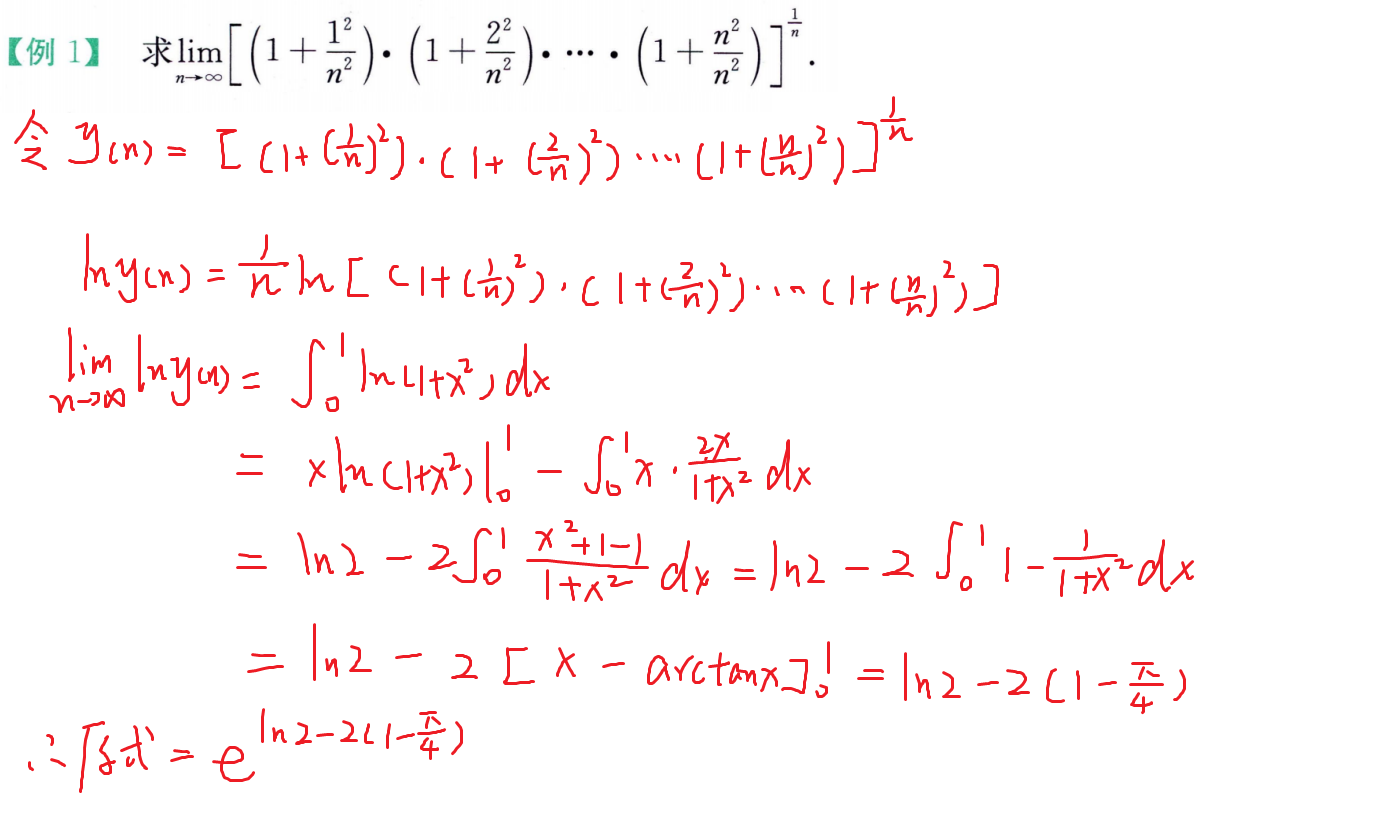
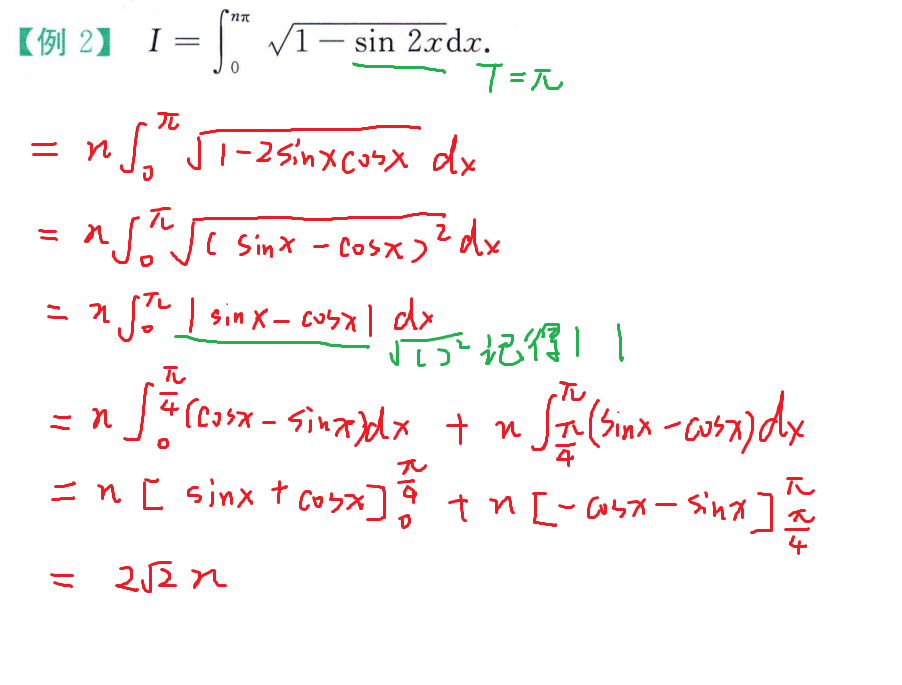
强化例题（变上限积分）

考点

连续性

若f(x)在[a, b]上可积，则∫(x, a) f(t) dt 在[a, b]上连续

可导性

奇偶性

例题

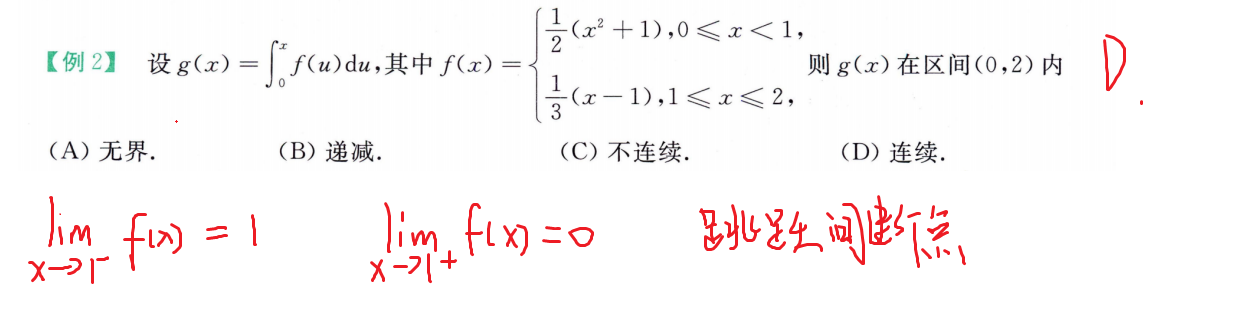
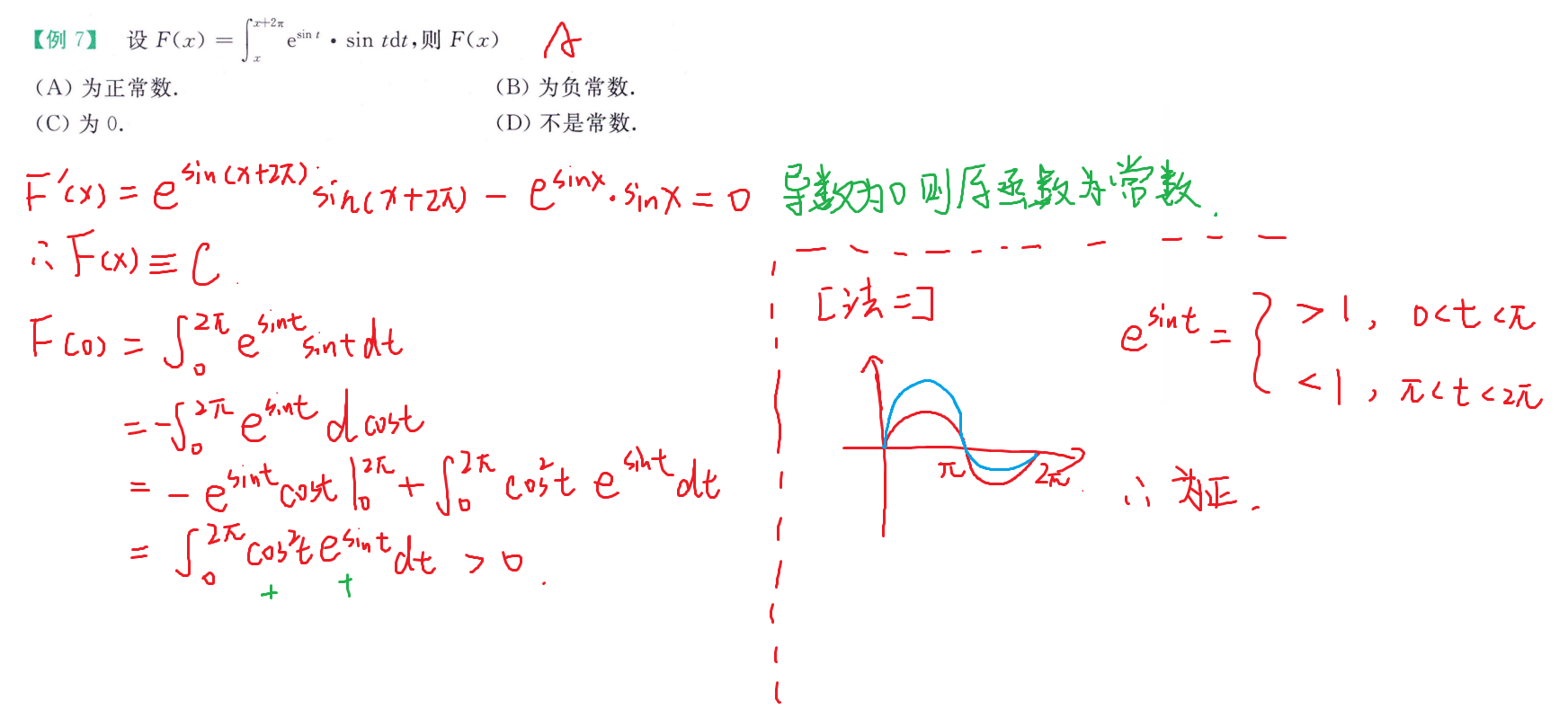
强化例题（积分不等式）

常用方法：

1. 定积分不等式

2. 变量代换

3. 积分中值定理

4. 变上限积分

5. 柯西积分不等式

   

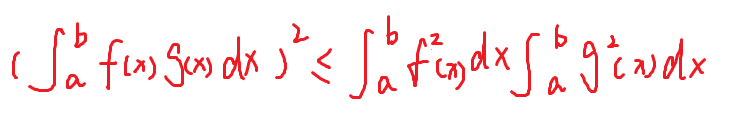
例题

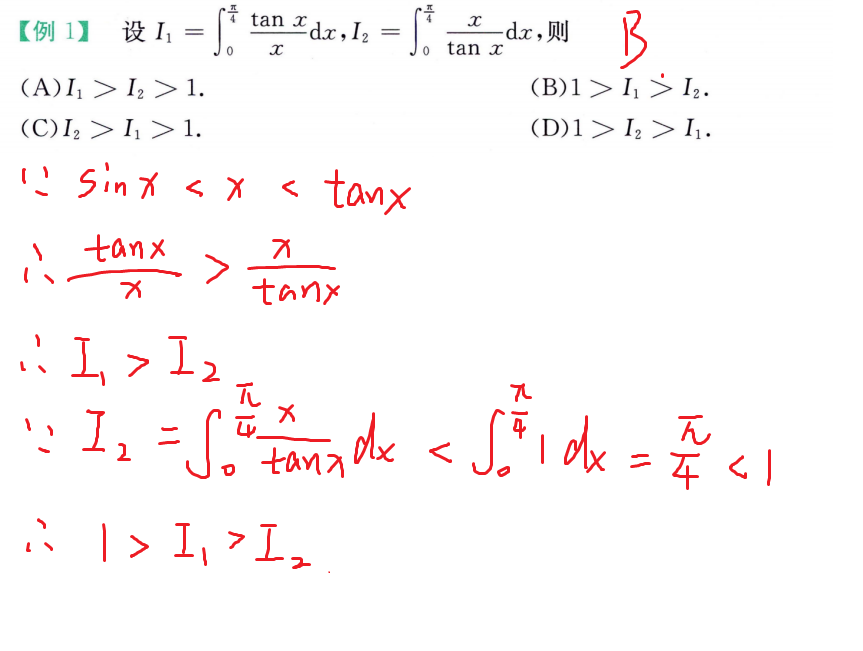
强化例题（反常积分）

考点

无穷区间上的反常积分

无界函数的反常积分

伽马函数

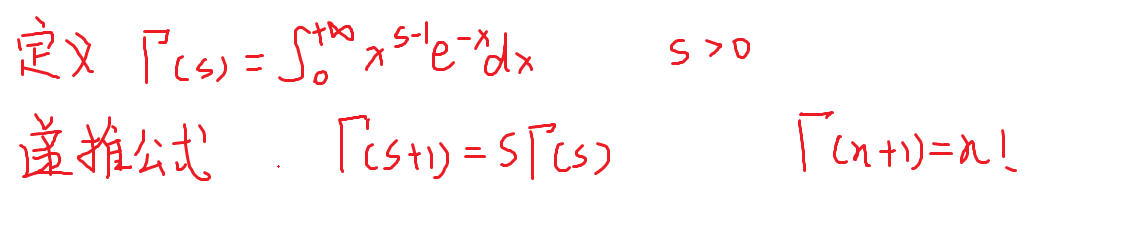
例题

判断敛散性

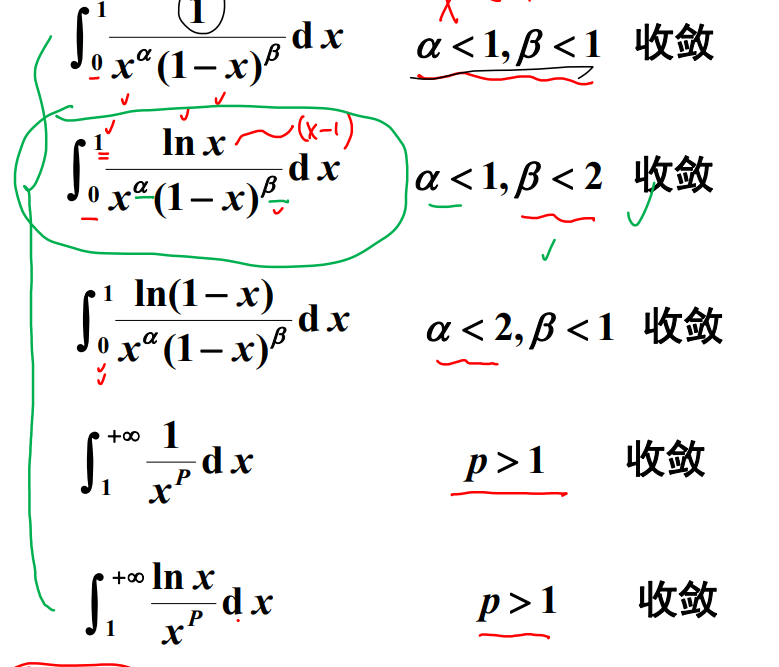
反常积分计算

强化例题（定积分应用）

例题

几何应用

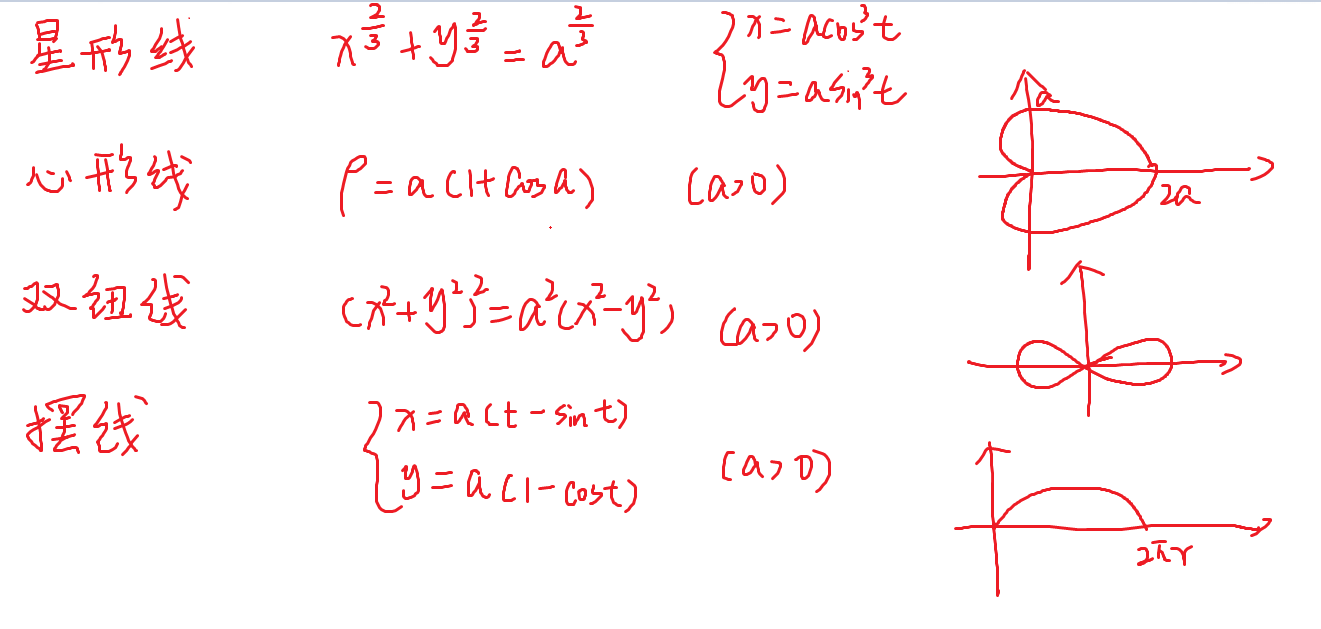
物理应用

强化例题（常微分方程）

强化例题（一阶微分方程）

常见题型

可分离变量方程

形式：y’ = f(x)g(y)

解法：分离变量，两端积分。g(y)dy = f(x)dx

齐次方程

形式：dy / dx = φ(y/x)

解法：令u = y/x，y’ = u + xu’，从而化为可分离变量

一阶线性方程

形式：y’ + P(x)y = Q(x)

解法：套公式

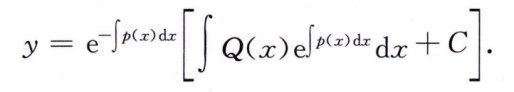
伯努利方程

形式：y’ + P(x)y =Q(x)y^n

解法：令u = y^(1 - n)化为一阶线性方程

全微分方程

形式：du(x, y) = P(x, y)dx + Q(x, y)dy

不是上面的题型，则可尝试x、y对调或变量代换

例题

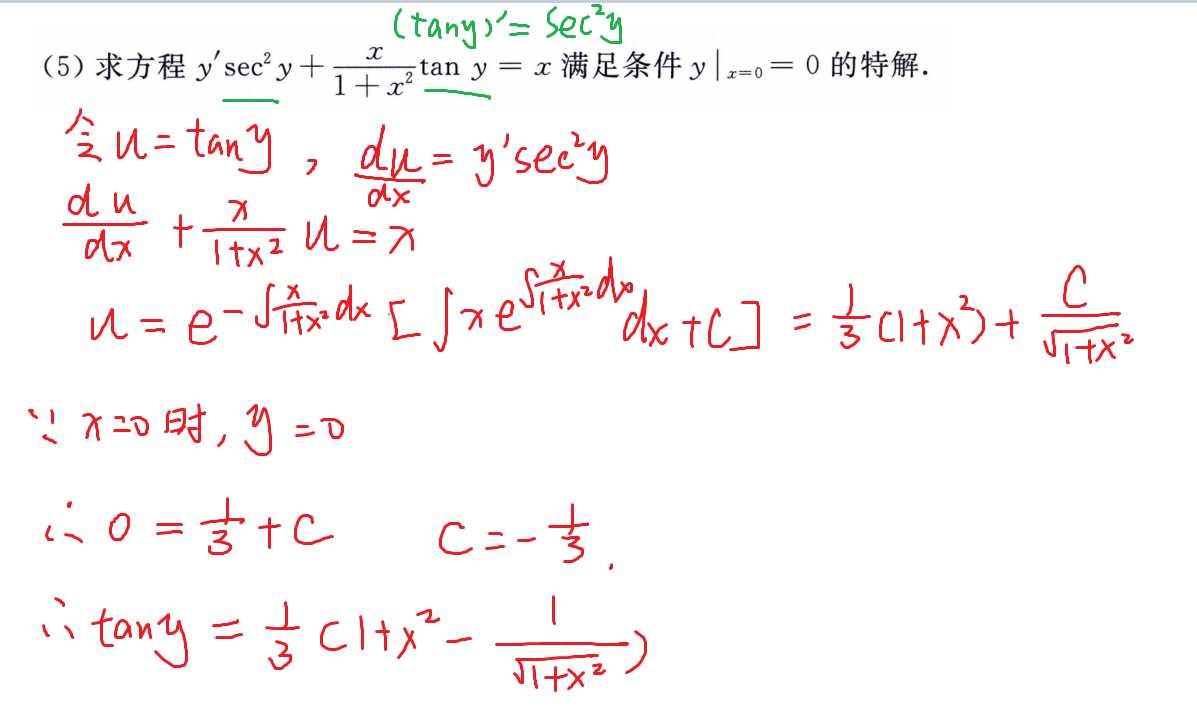
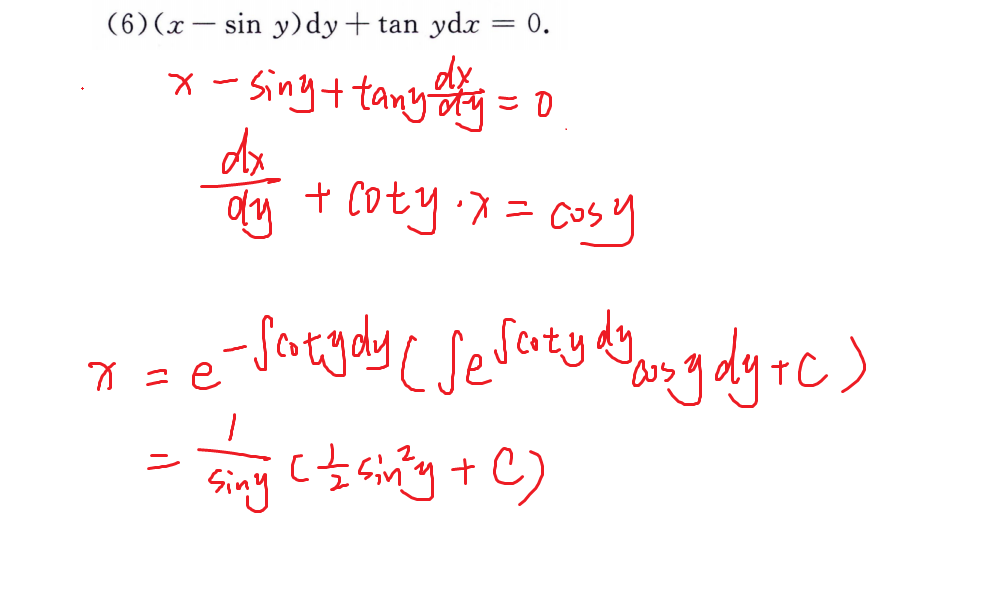
强化例题（可降阶的高阶方程）

常见题型

y’’ = f(x)：两边求积分

y’’ = f(x, y’)：y’ = p, y’’ = dp / dx

y’’ = f(y, y’)：y’ = p, y’’ = p (dp/dy)

例题

强化例题（高阶线性方程）

常见题型

线性微分方程的解的结构

齐次方程：y’’ + p(x)y’ + q(x)y = 0

非齐次方程：y’’ + p(x)y’ + q(x)y = f(x)

两个线性无关特解C1 y1(x) + C2 y2(x) = y 为齐次通解

C1y1(x) + C2y2(x) + y*(x) = y 为非齐次通解

两个非齐次特解y1*(x) - y2 *(x) = y(x) 为齐次的解

常系数齐次线性微分方程通解

常系数非齐次线性微分方程特解

欧拉方程

例题

强化例题（综合题）

强化例题（多元函数微分）

强化例题（概念理论）

考点

重积分

定义：

点(x, y)在区域D内以任意方式趋近于(x0, y0)时，函数趋近于常数A，否则极限不存在

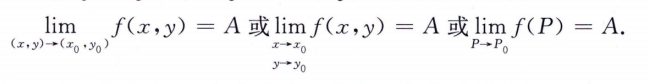
连续性

偏导数

定义：

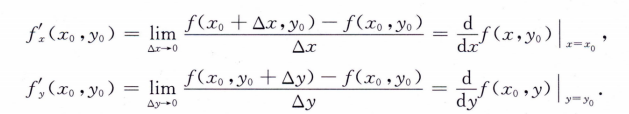
全微分

定义：

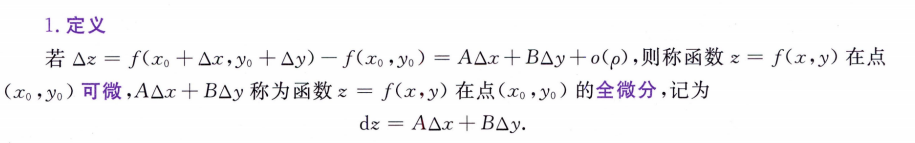
判断是否可微：

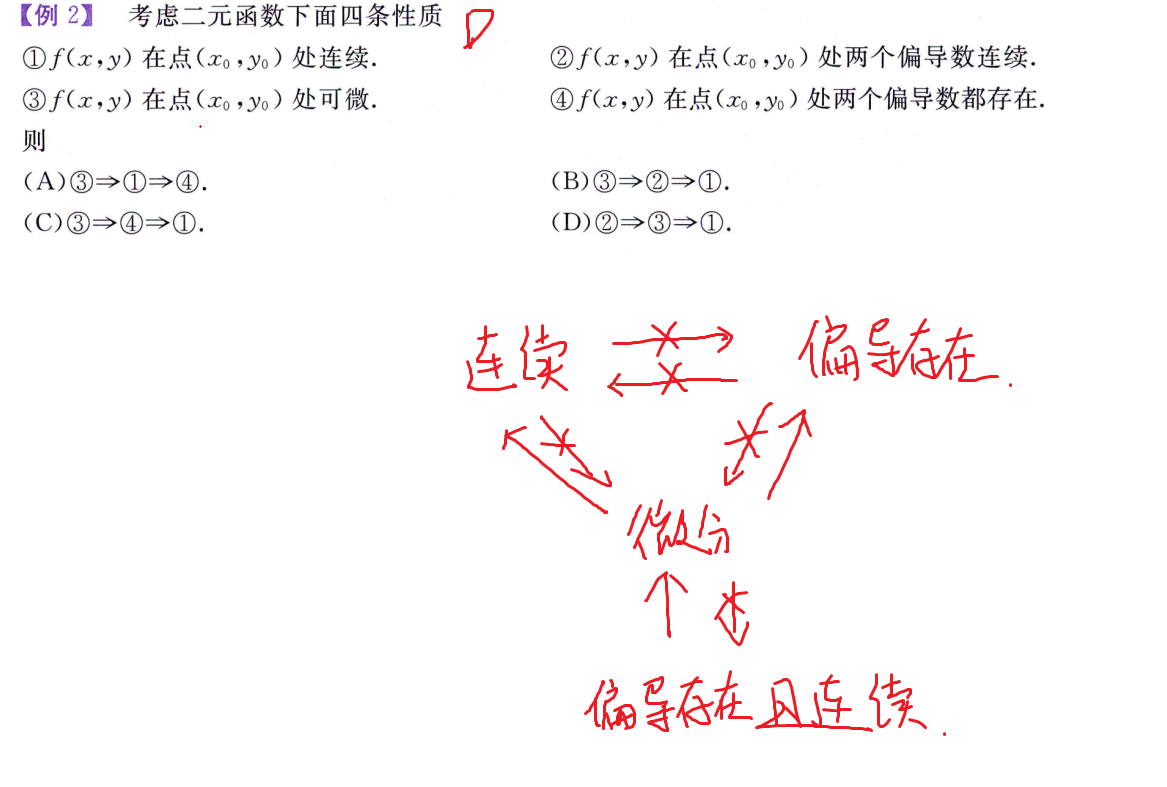
连续、可导、可微的关系：

例题

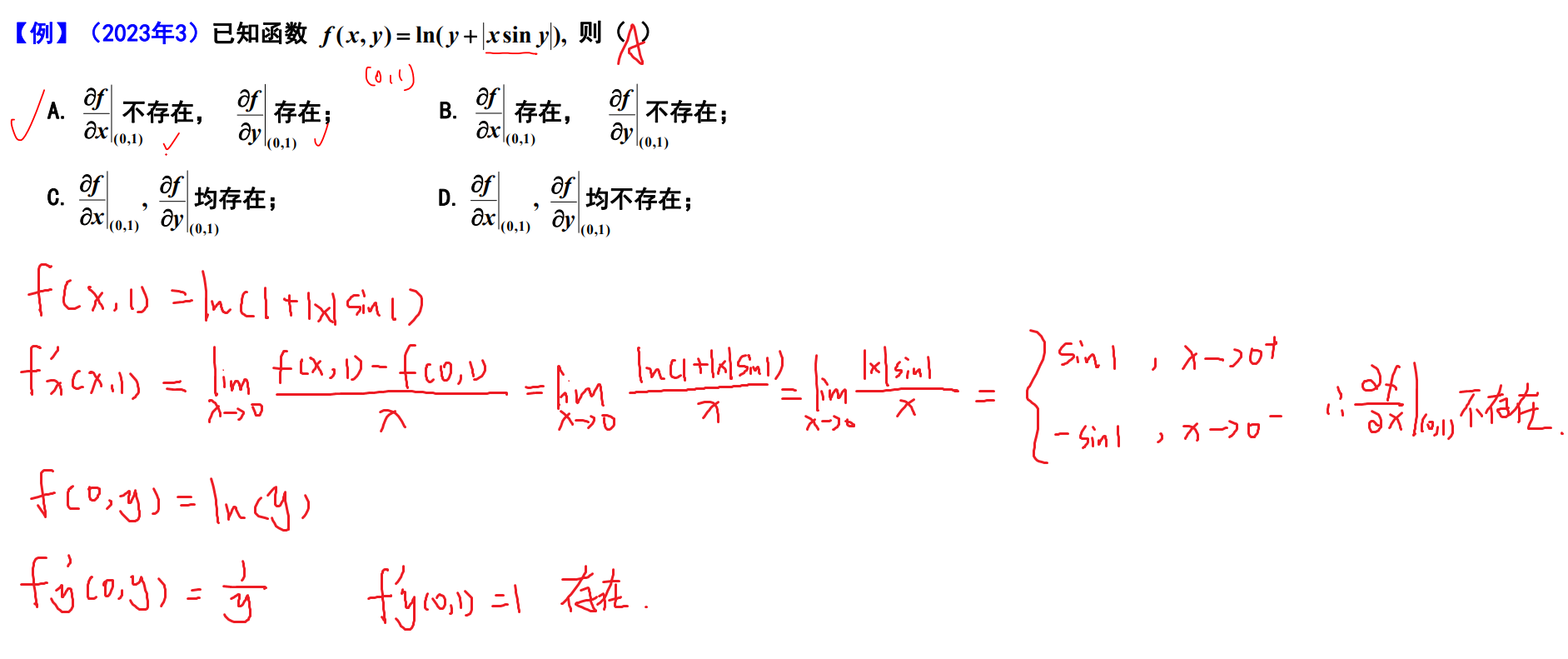
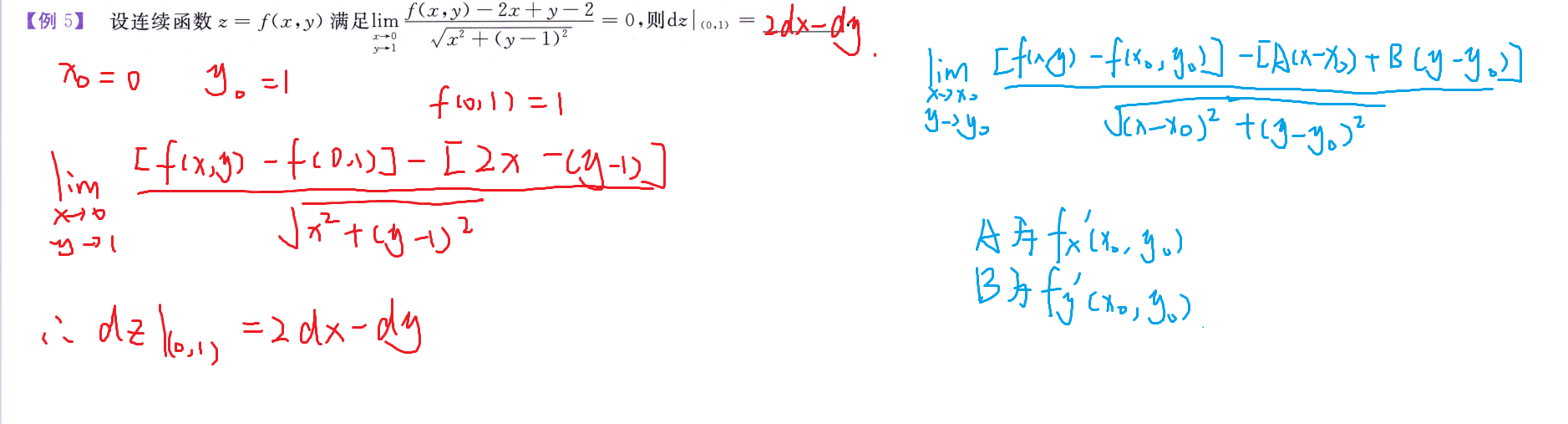
强化例题（计算）

考点

链式求导法

全微分形式不变性

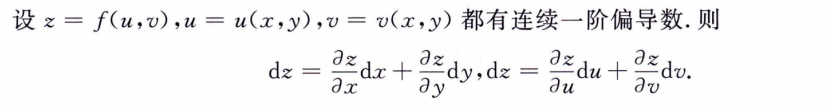
隐函数求导法

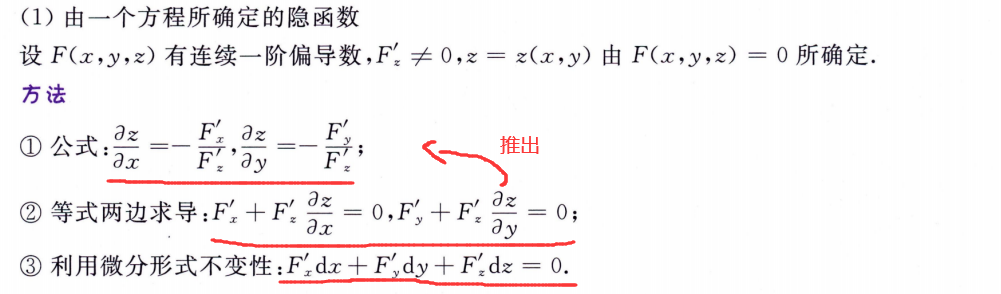
例题

求一点处的偏导数和全微分

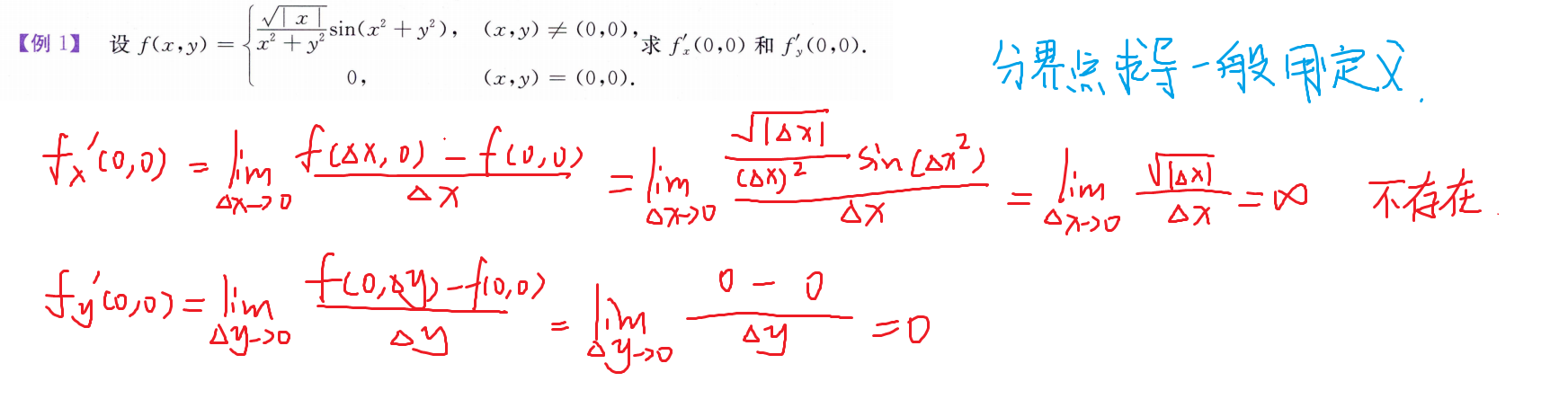
求给出具体函数的偏导数和全微分

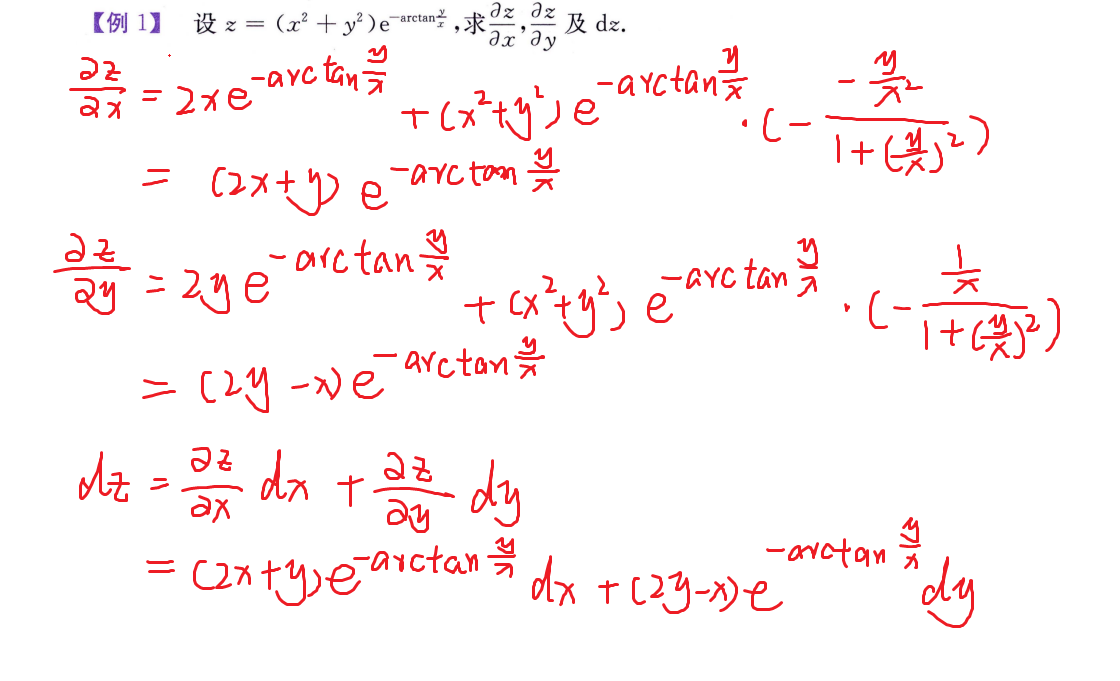
含有抽象函数的复合函数的偏导数和全微分

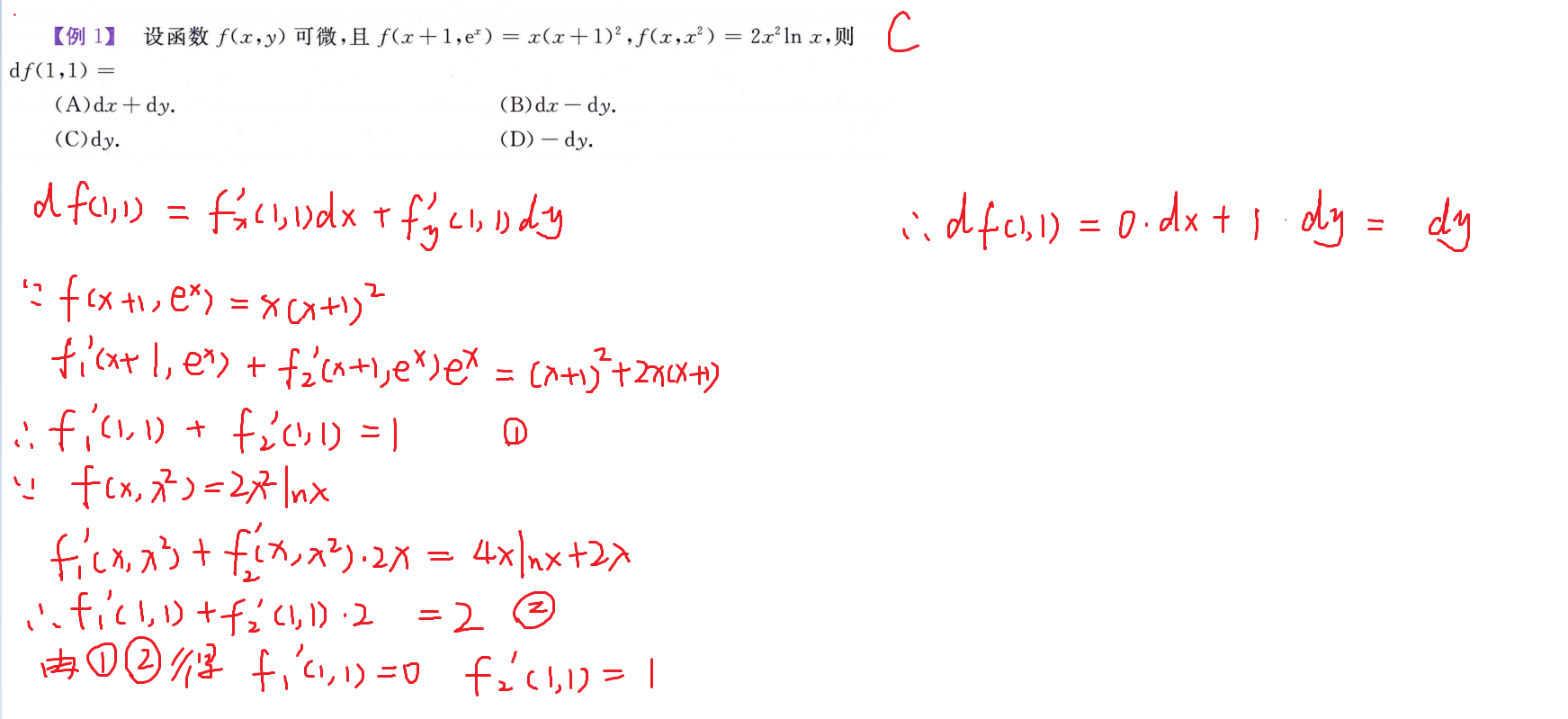
隐函数的偏导数和全微分

强化例题（极值最值）

考点

无条件极值

条件极值

最值

找最值方法：

1. 找出区域D内部可能的极值点
2. 找出区域D边界上可能的极值点
3. 比较

例题

无条件极值

最大最小值

强化例题（二重积分）

例题

二重积分计算

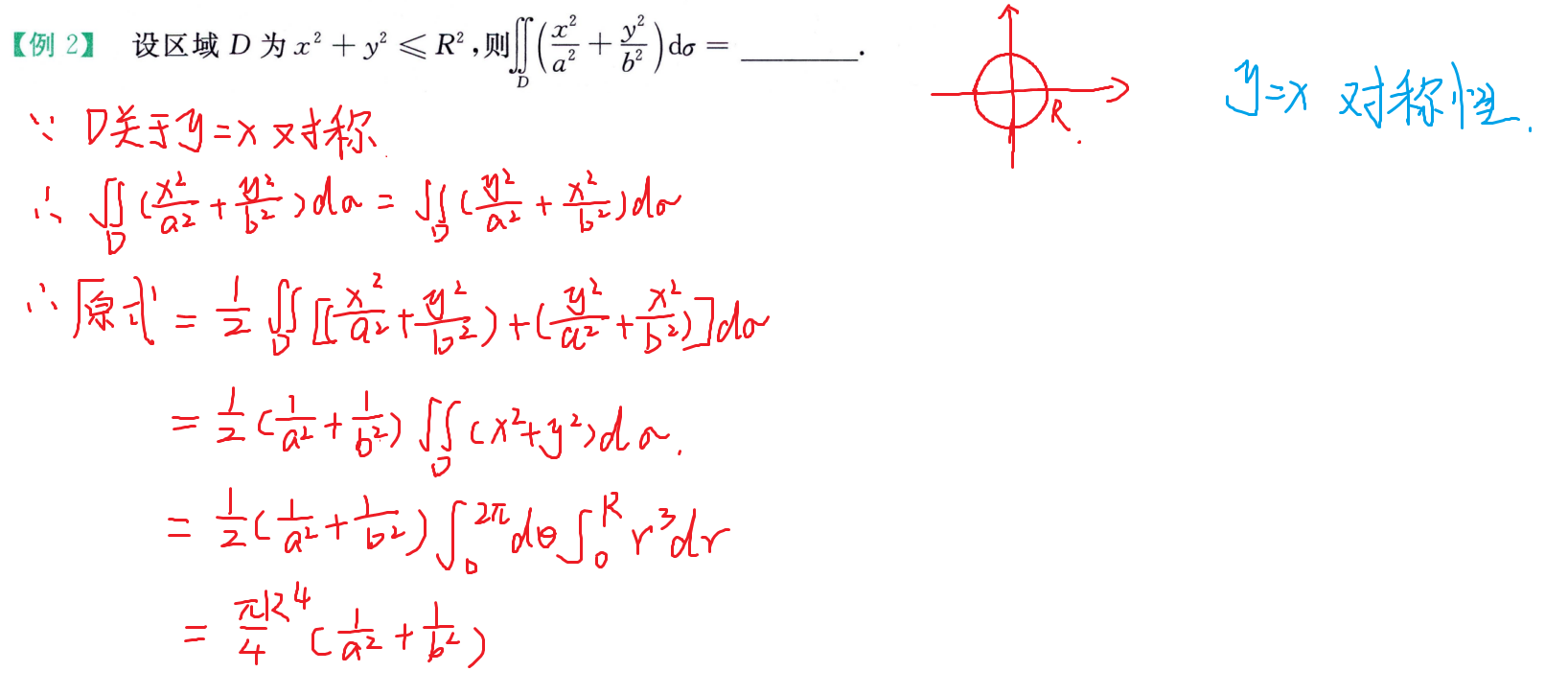
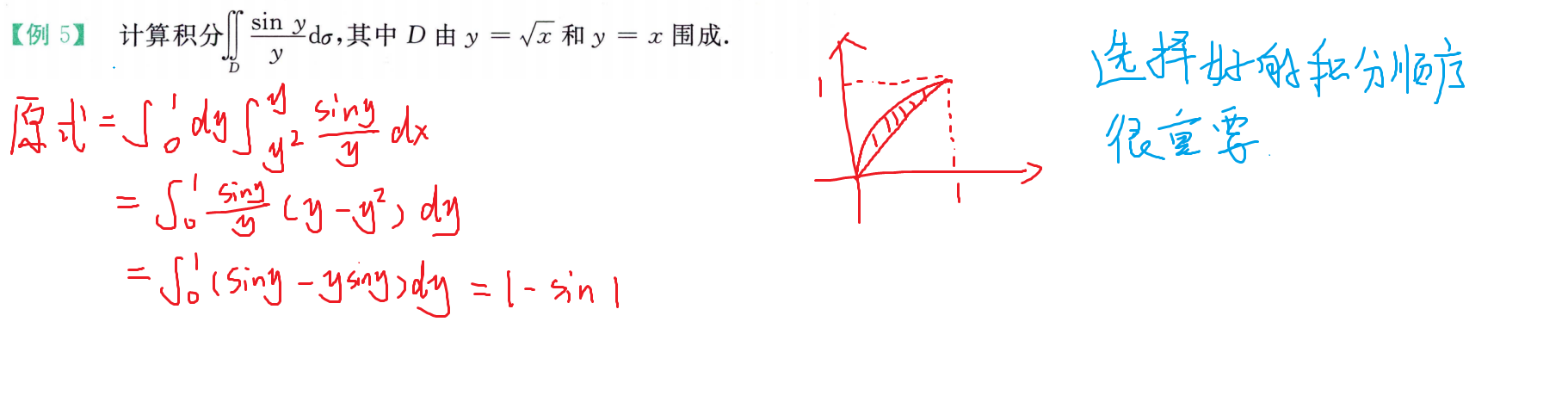
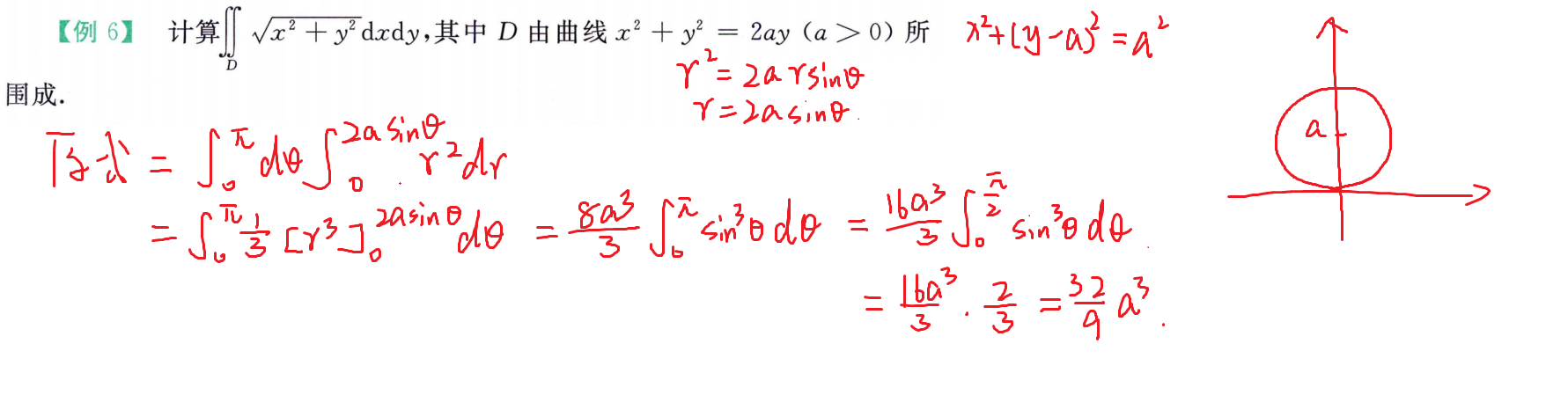
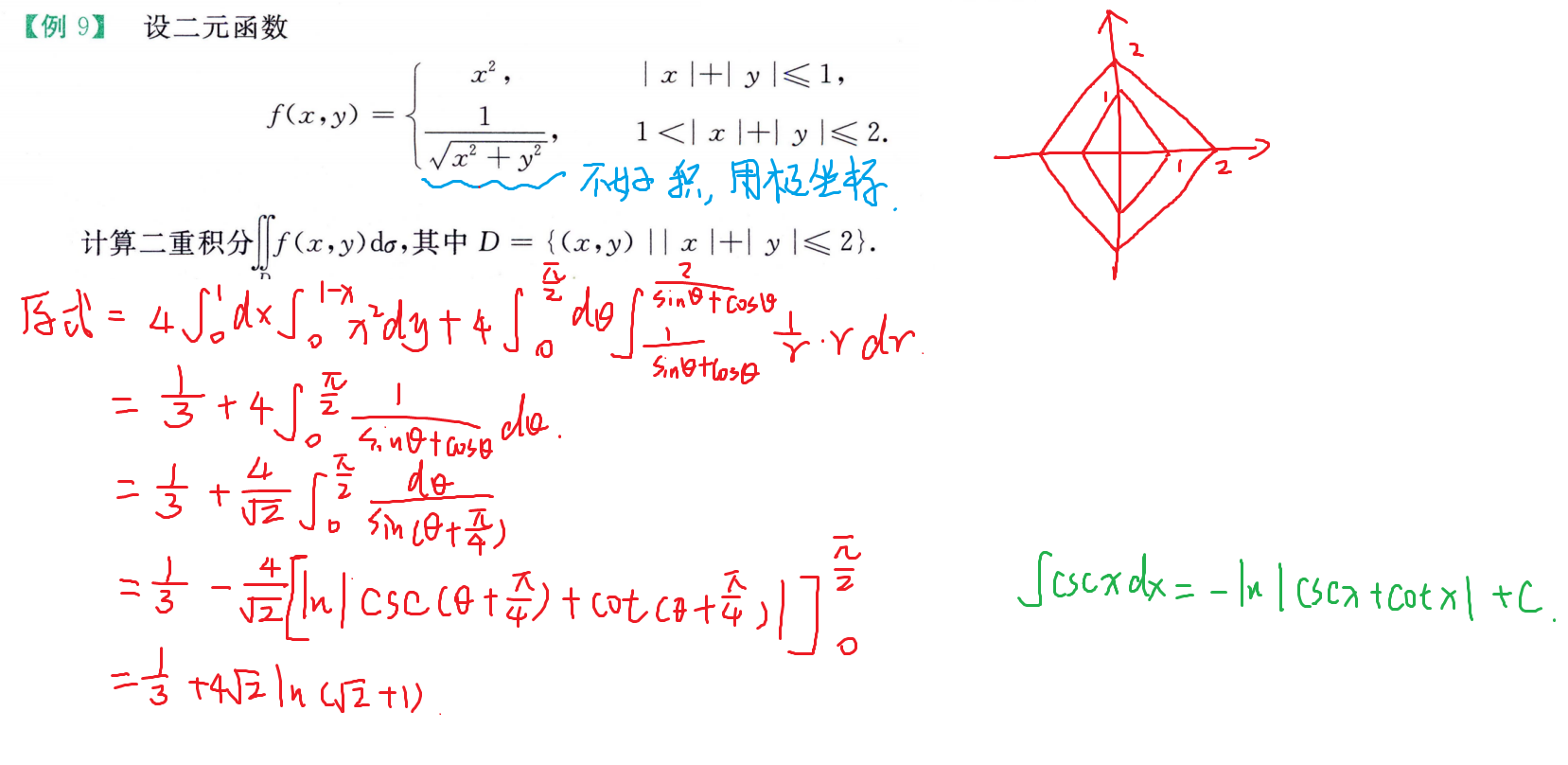
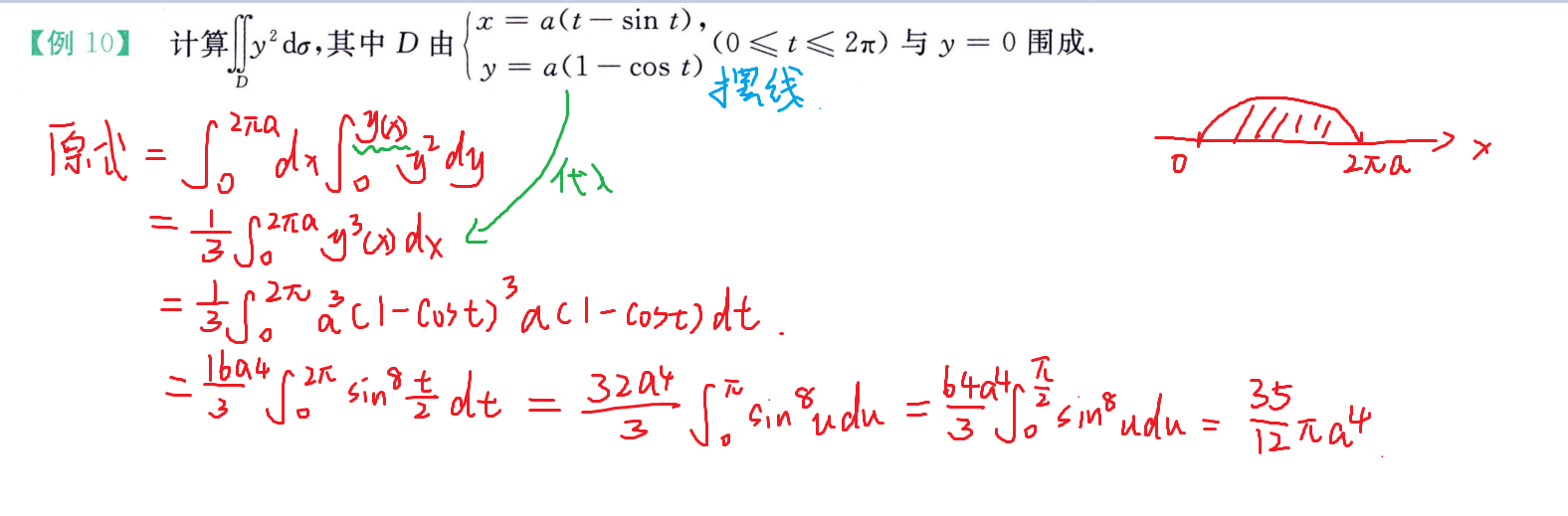
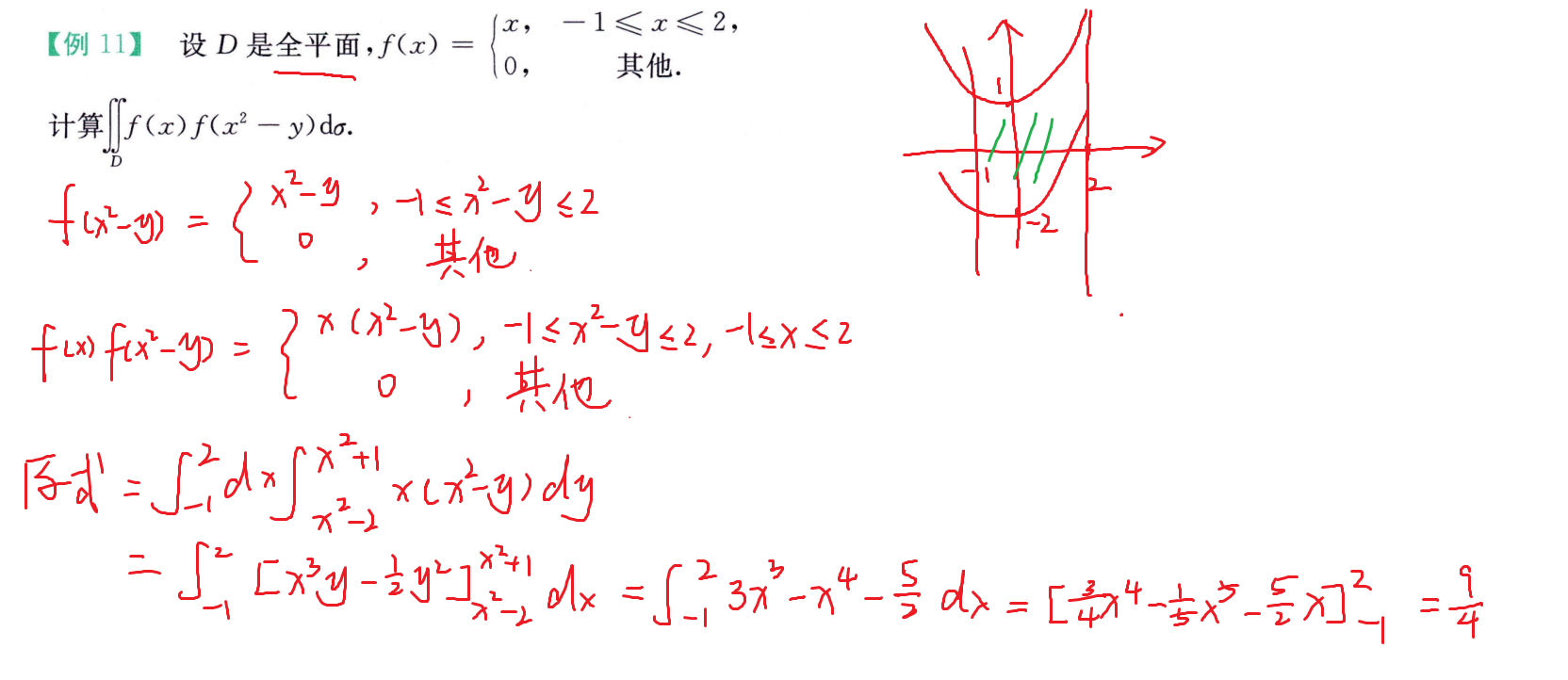
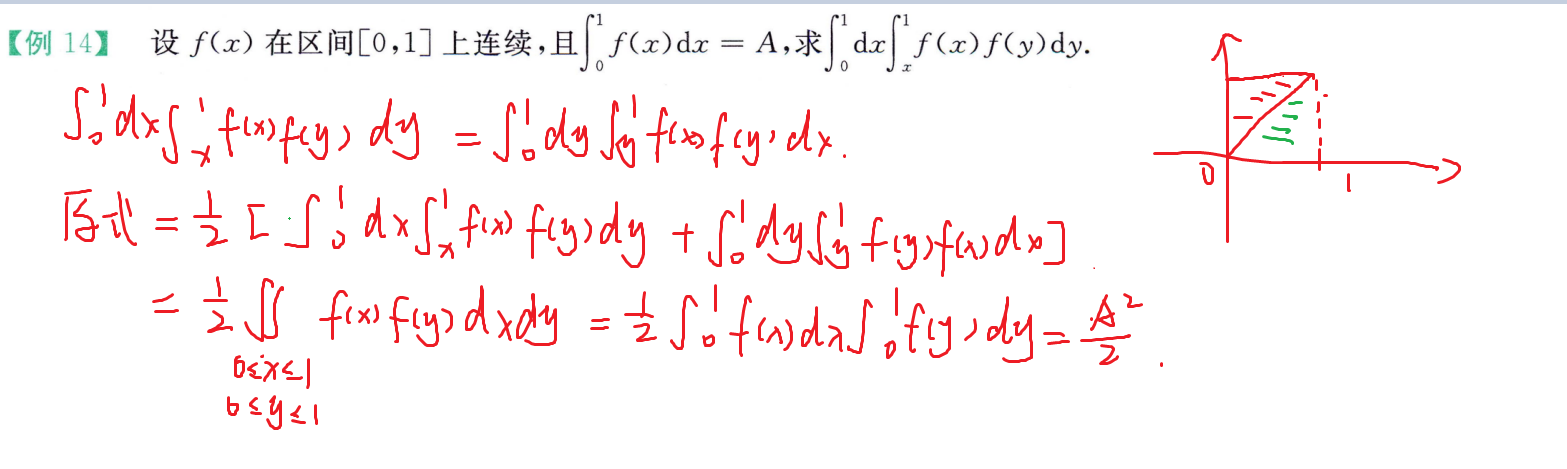
交换积分次序

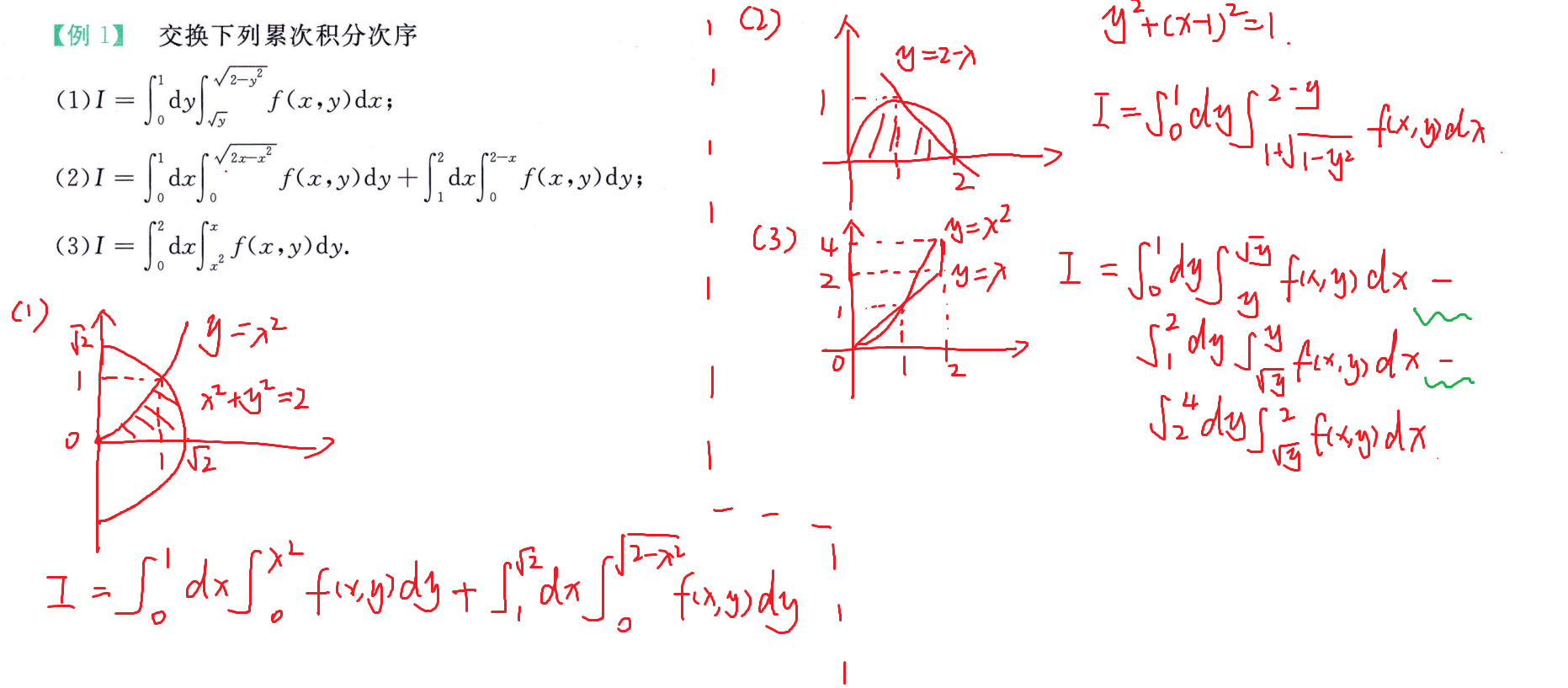
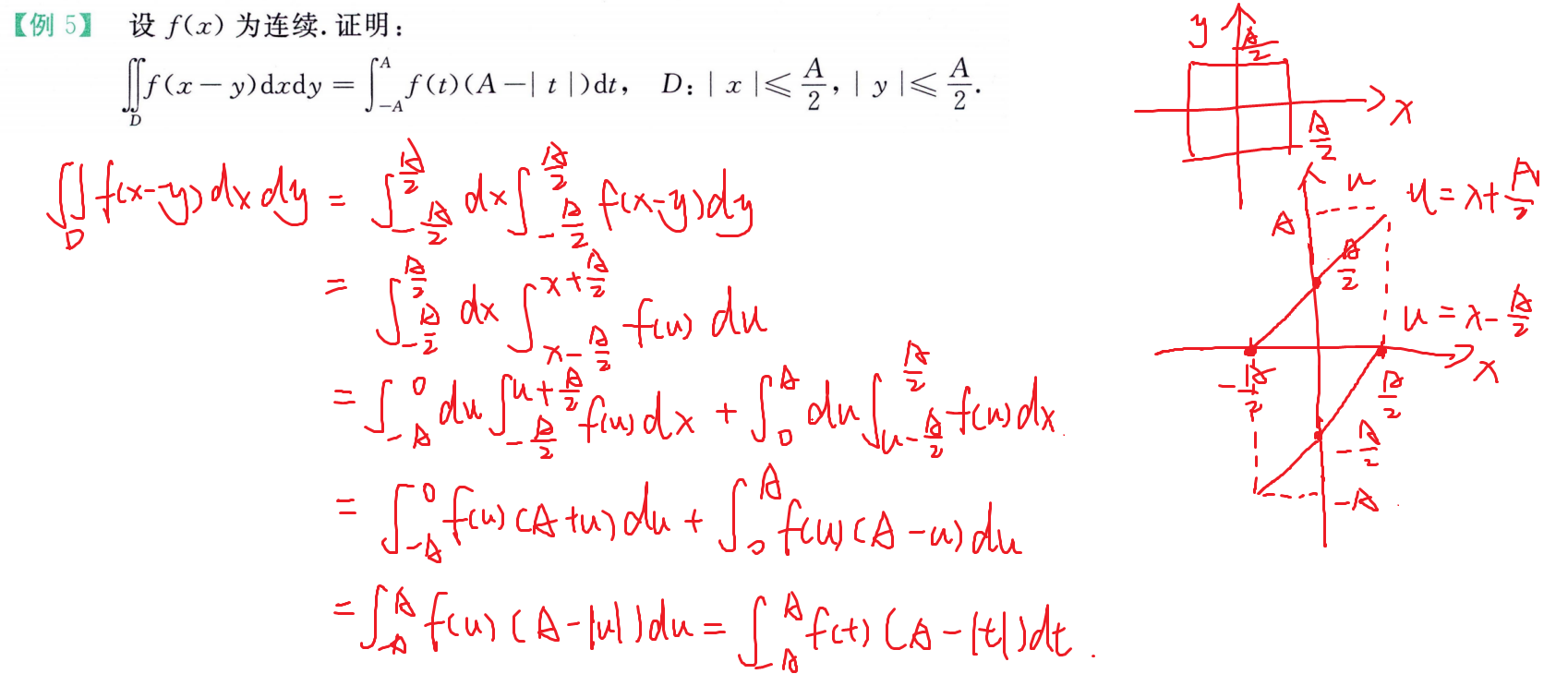
综合题

不等式问题

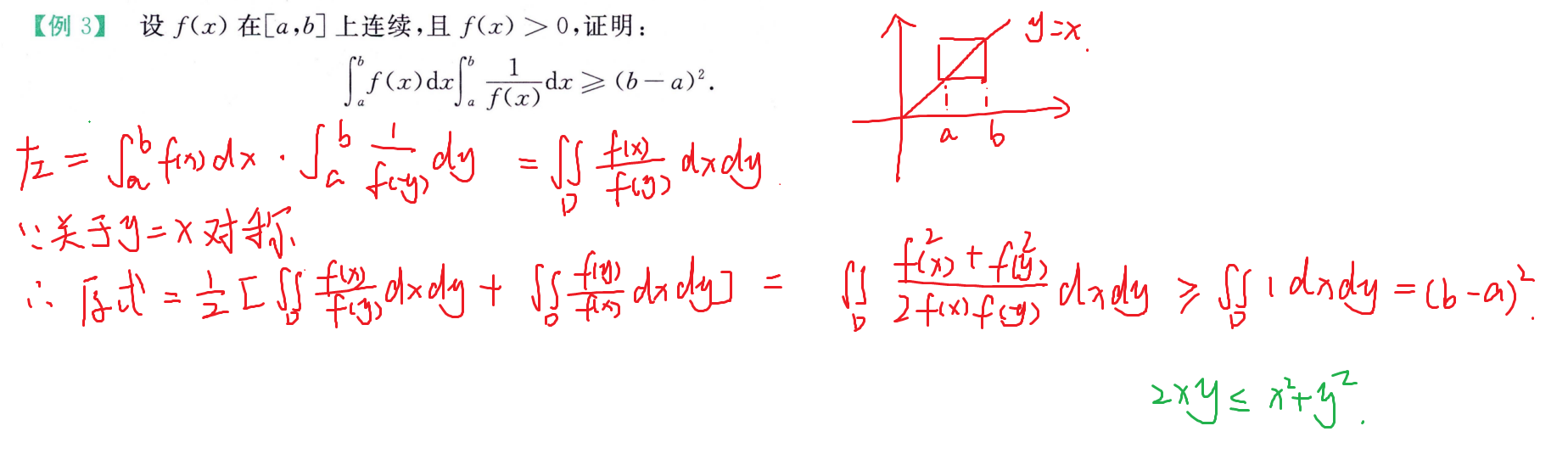
强化例题（无穷级数）

概念

级数审敛法✨

正项级数的判别法

正项级数：每项都 > 0

1. 比较判别法

   大的收敛，小的必收敛；小的发散，大的必发散。

2. 比较法极限形式

   

3. 比值法

   

4. 根值法

   

5. 积分判别法

   少部分题好用

   

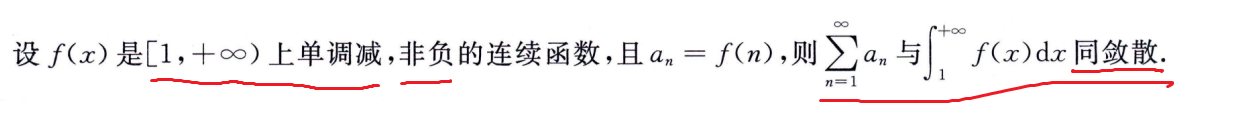
交错级数的判别法

交错级数：每项正负交替

1. 莱布尼兹准则

   

任意项级数

任意项级数：每项为任意实数

绝对收敛：加了绝对值收敛，则原函数必收敛

条件收敛：原级数收敛，但加了绝对值发散

绝对收敛的条件要求更高

条件收敛的级数的所有正项（负项）构成的级数一定发散

例题

正项级数

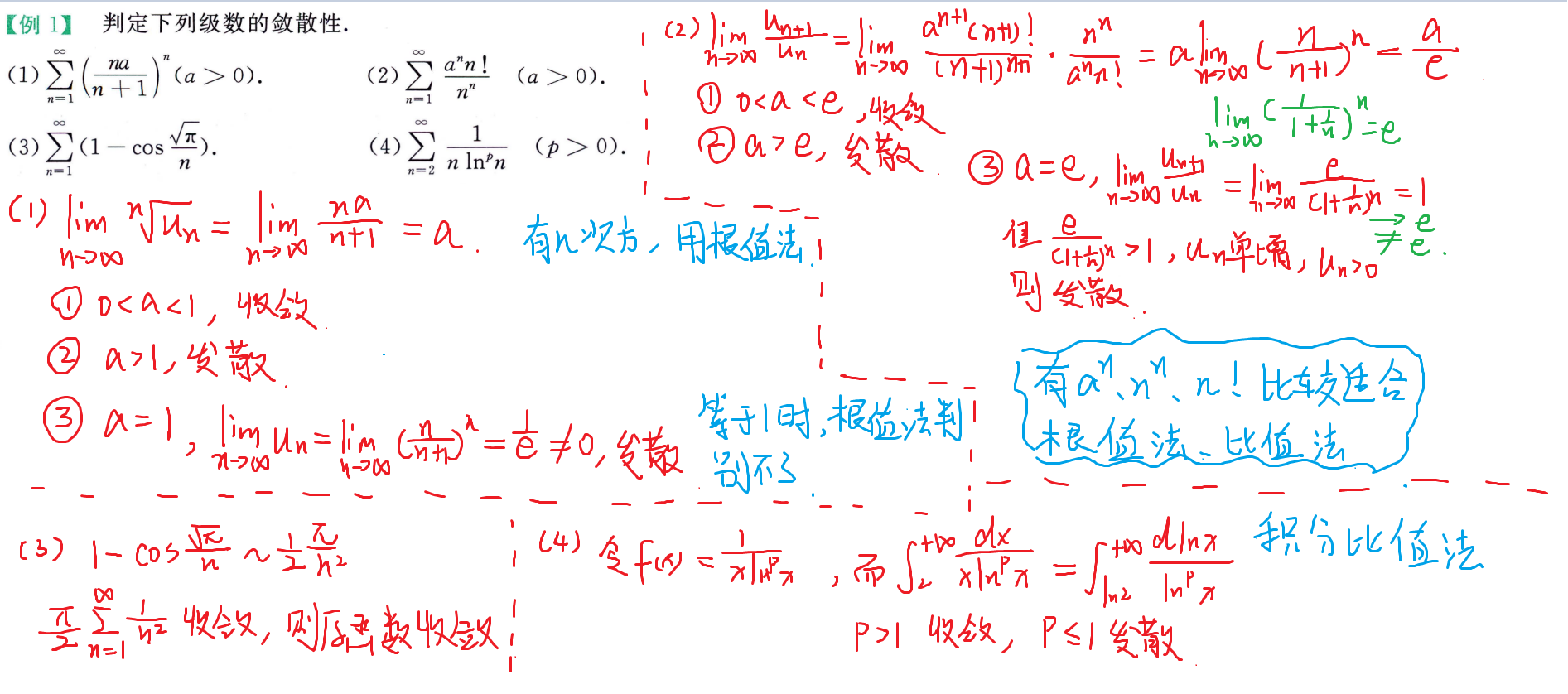
交错级数

任意项级数

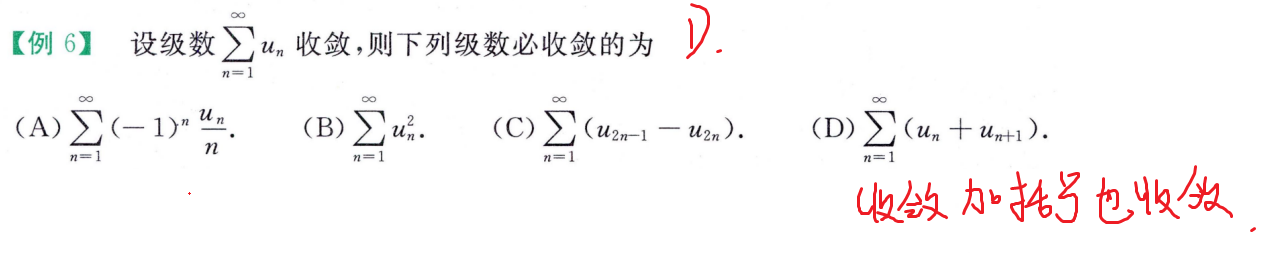
综合题

强化例题（幂级数）

概念

幂级数

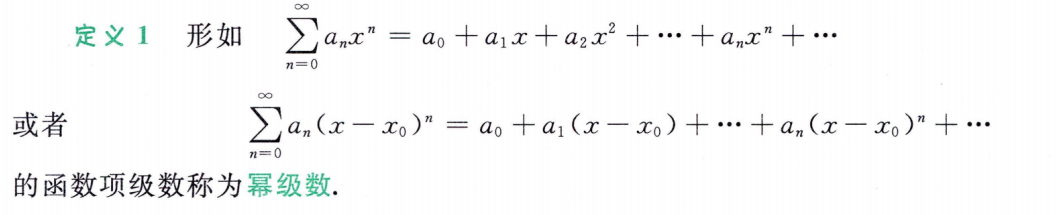
阿贝尔定理

收敛半径、收敛区间和收敛域

幂级数性质

函数的幂函数展开

将函数在收敛半径内展开为幂函数

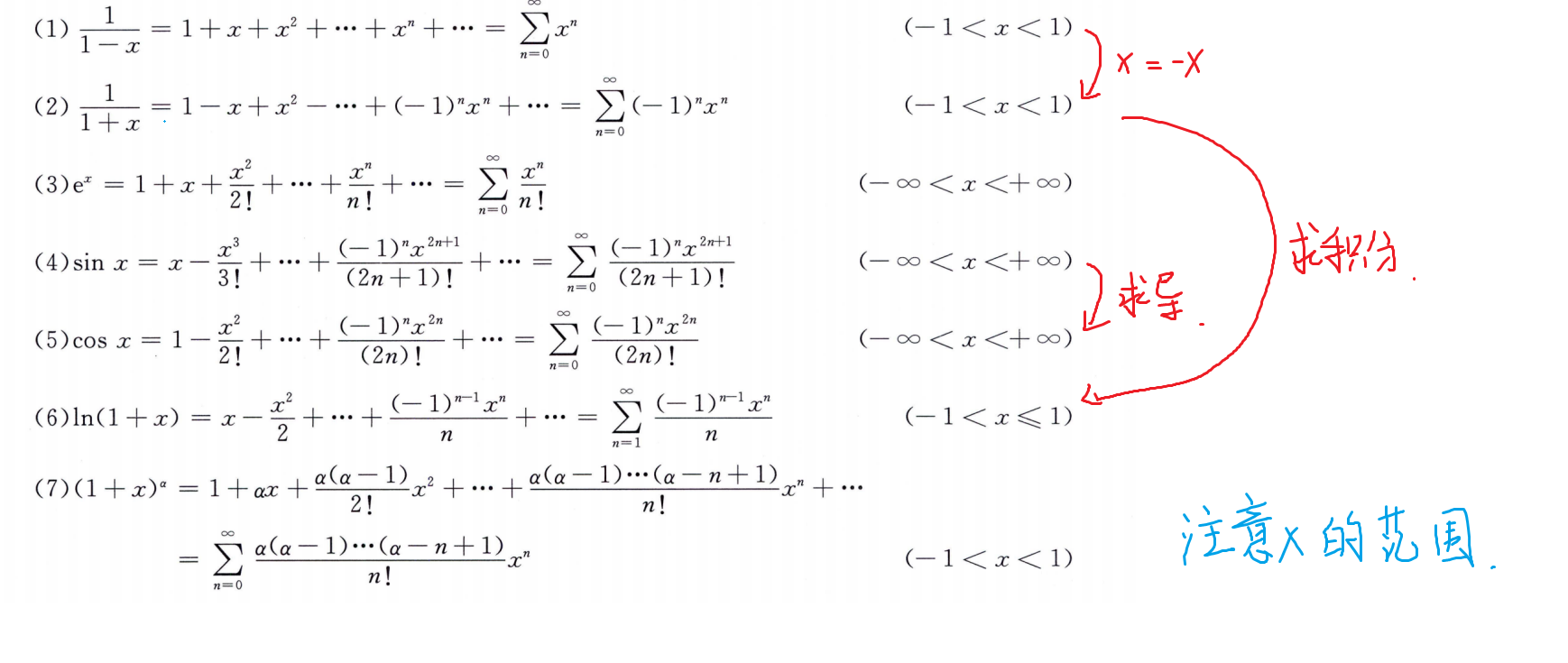
幂函数展开方法：

1. 直接法：求出各阶导数，泰勒级数，再判断余项是否为0
2. 间接展开法：向已有的展开式的形式靠近

例题

求收敛区域和收敛域

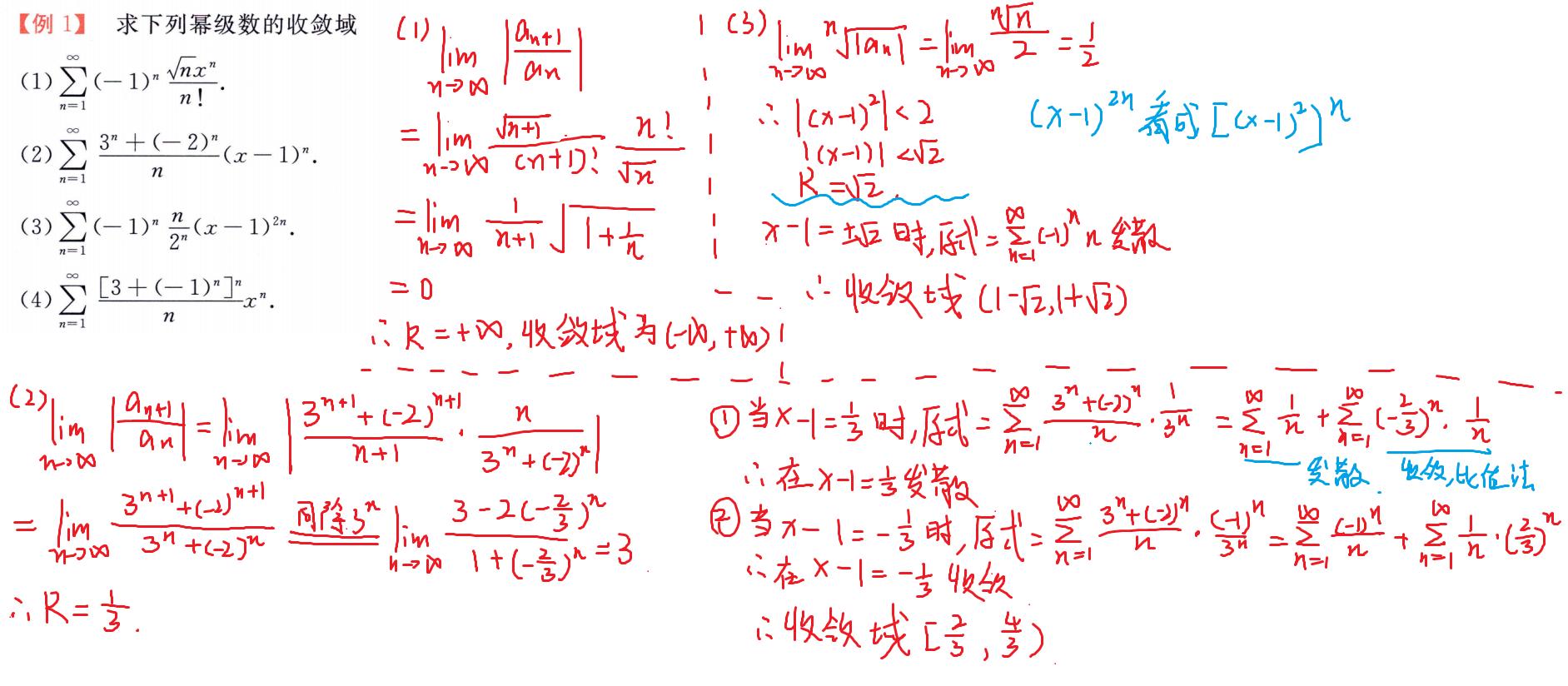
函数展开为幂级数

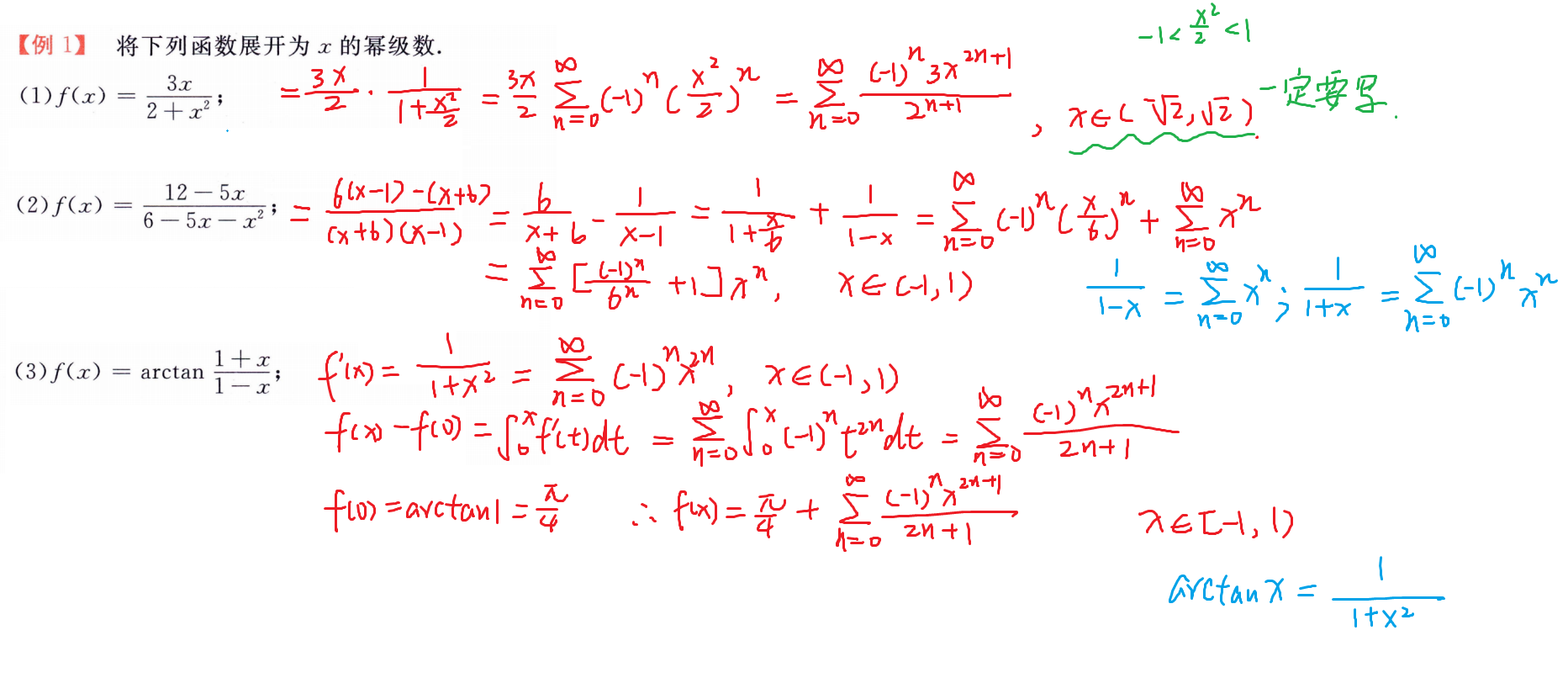
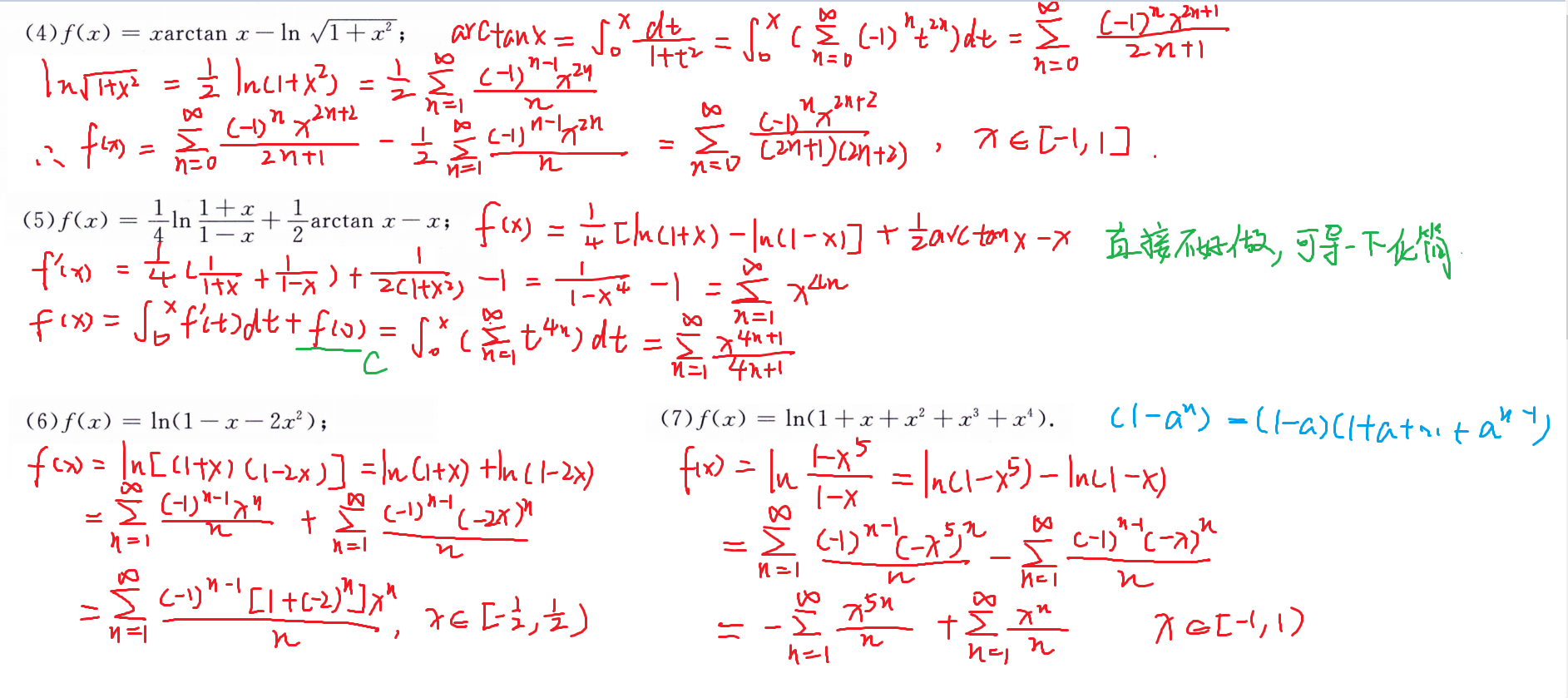
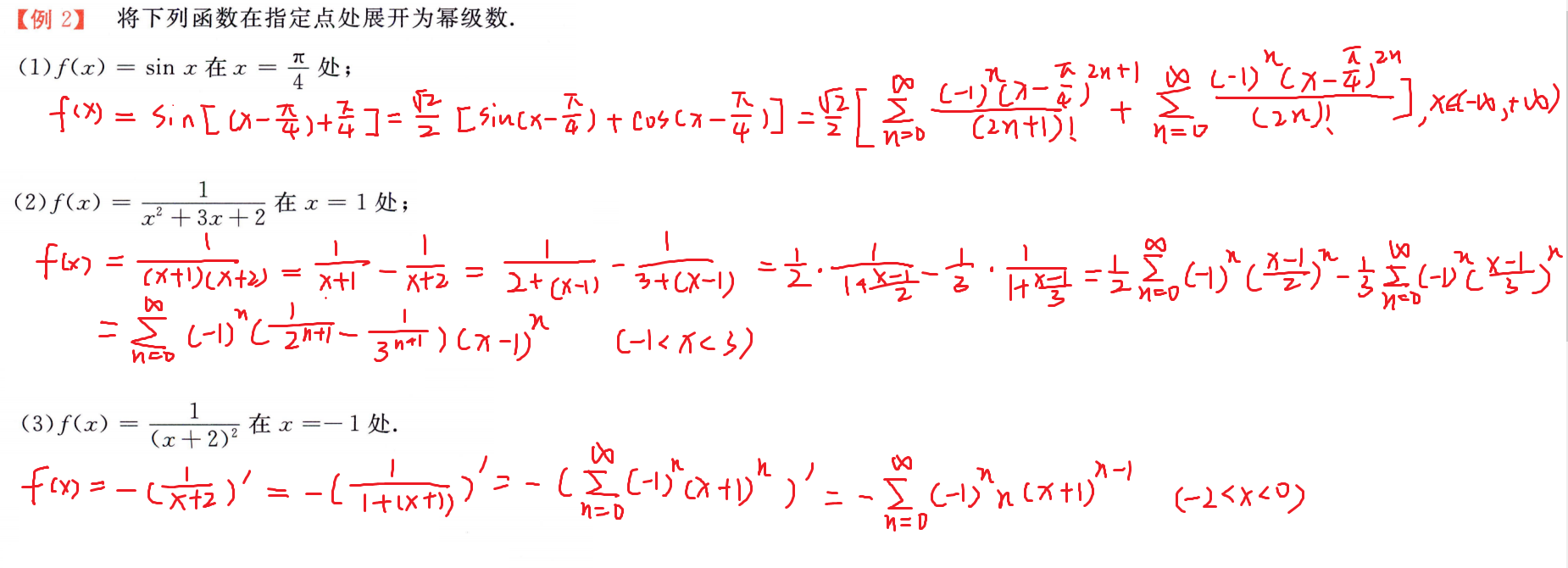
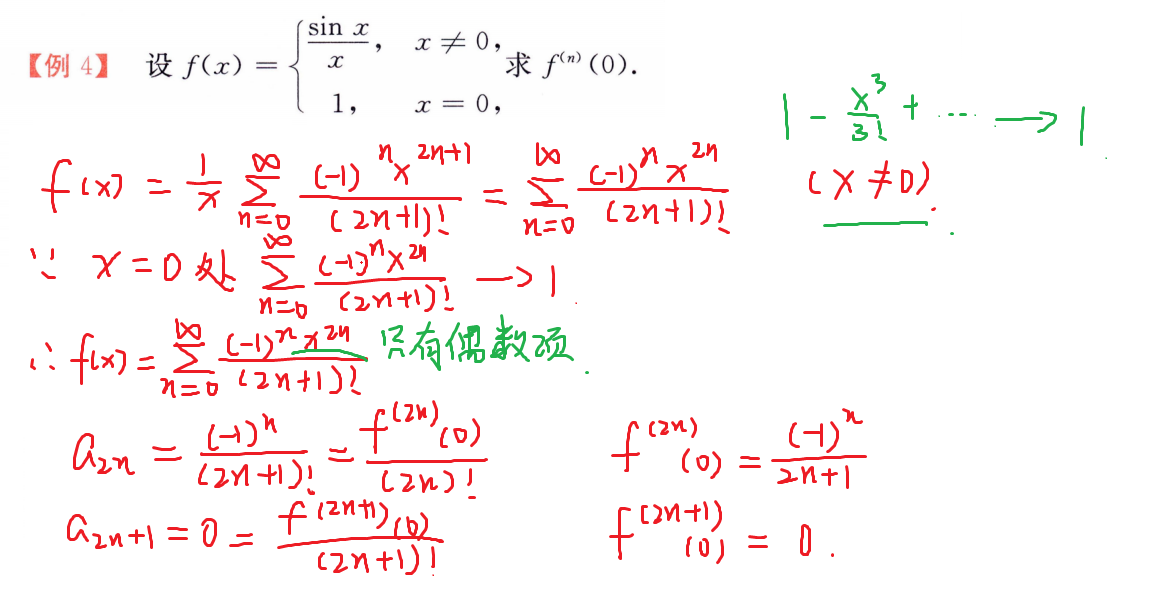
级数求和

强化例题（傅里叶级数）

概念

傅里叶系数和傅里叶级数

收敛定理

周期为2π的函数展开为傅里叶级数

周期为2l的函数展开为傅里叶级数

例题

收敛定理

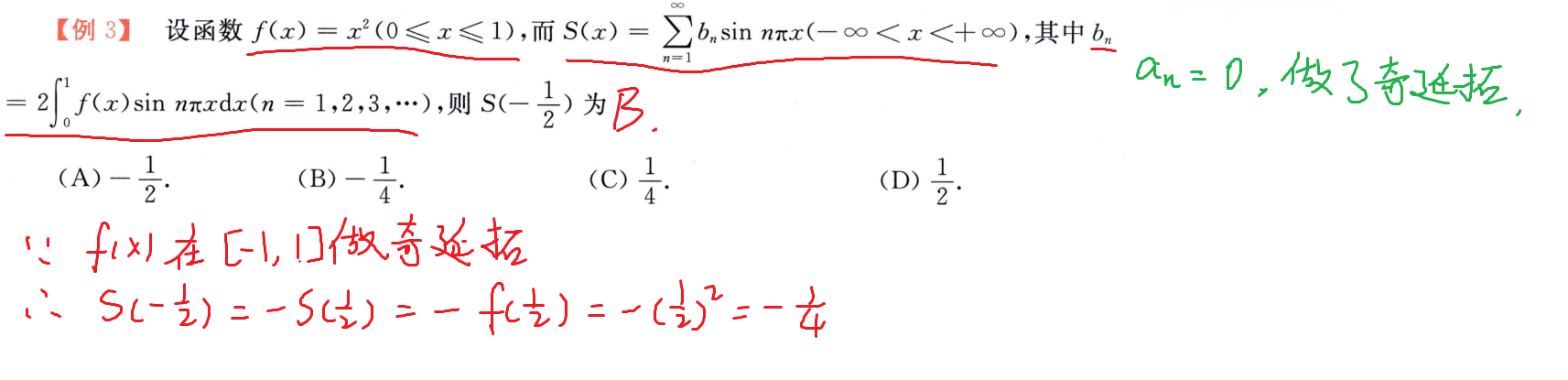
函数展开为傅里叶级数

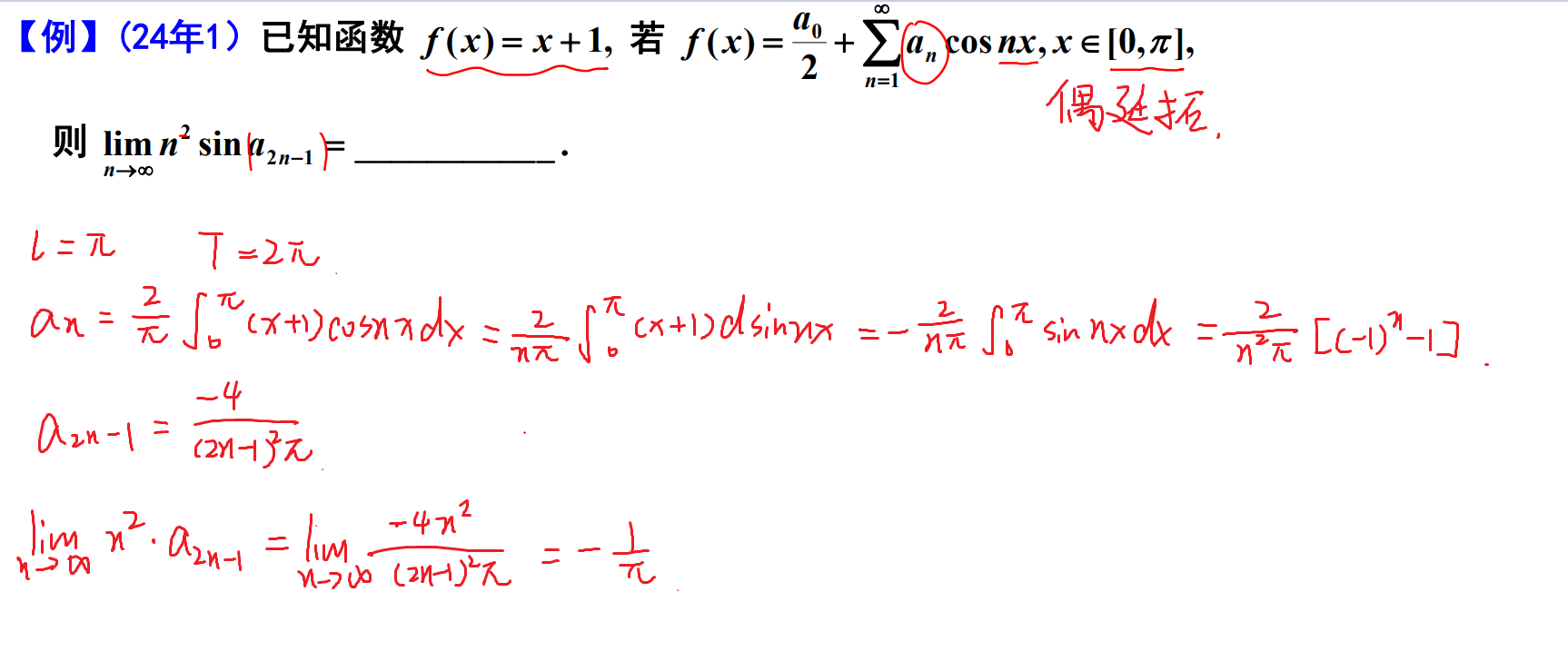
强化例题（空间几何）

概念

向量代数

数量积

a ・ｂ = |a| |b| cosθ

a ・ｂ = axbx +ayby + azbz

判定两向量垂直：a ・ｂ = 0

向量积

|a x b| = |a| |b| sinθ

判定两向量平行：a x b = 0

混合积

(abc) = (a x b)・c

几何上表示六面体体积

判定三向量共面：(abc) = 0

轮换对称性：(abc) = (bca) = (cab)

交换变号：(abc) = -(acb)

空间直线和平面

曲面与空间曲线

多元函数微分在几何上的应用

方向导数和梯度

例题

向量代数

向量运算

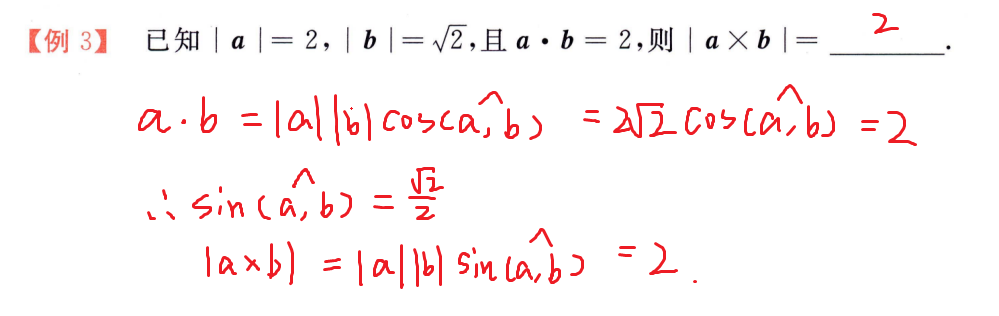
向量运算的应用

空间直线和平面

重点在直线的方向向量和平面的法向量

建立直线方程

建立平面方程

曲面与空间曲线

多元函数微分在几何上的应用

方向导数和梯度

强化例题（多元函数积分）

概念

三重积分

三种坐标轴

1. 直角坐标

2. 柱面坐标

   

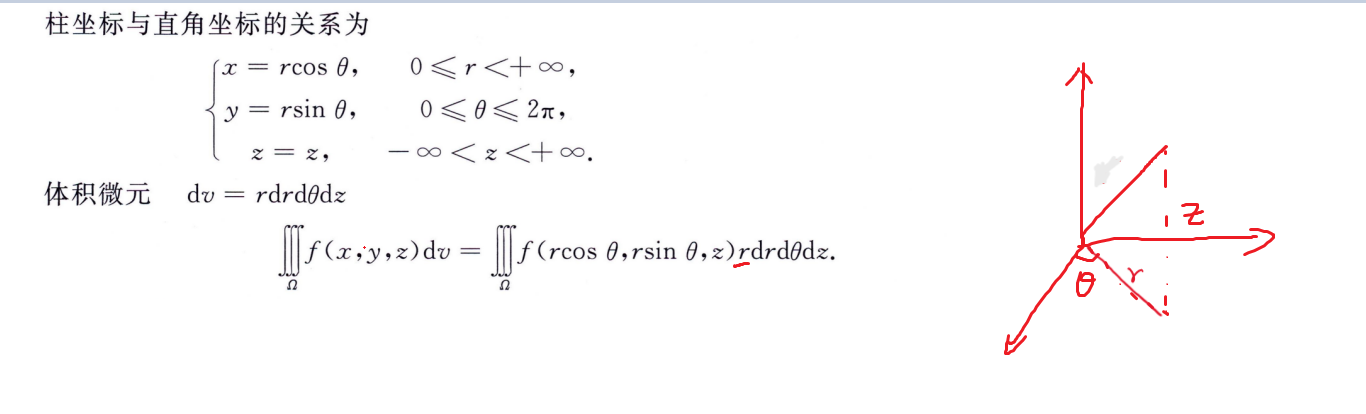
3. 球坐标

   

对弧长的线积分（第一类积分）

求弧的质量，与积分路径无关

计算方式

对坐标的线积分（第二类积分）

求变力在弧线上做功，与积分路径有关

计算方法

线积分与路径无关的判定

对面积的面积分（第一类面积分）

值与积分曲面的方向无关

计算：

1. 直接法

   

2. 奇偶性

3. 对称性

对坐标的面积分（第二类面积分）

值与积分曲面的方向有关

计算：

1. 直接法

   

2. 高斯公式

   

3. 补面用高斯公式

两类面积分的联系

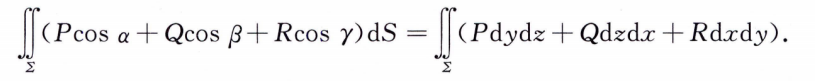
例题

三重积分计算

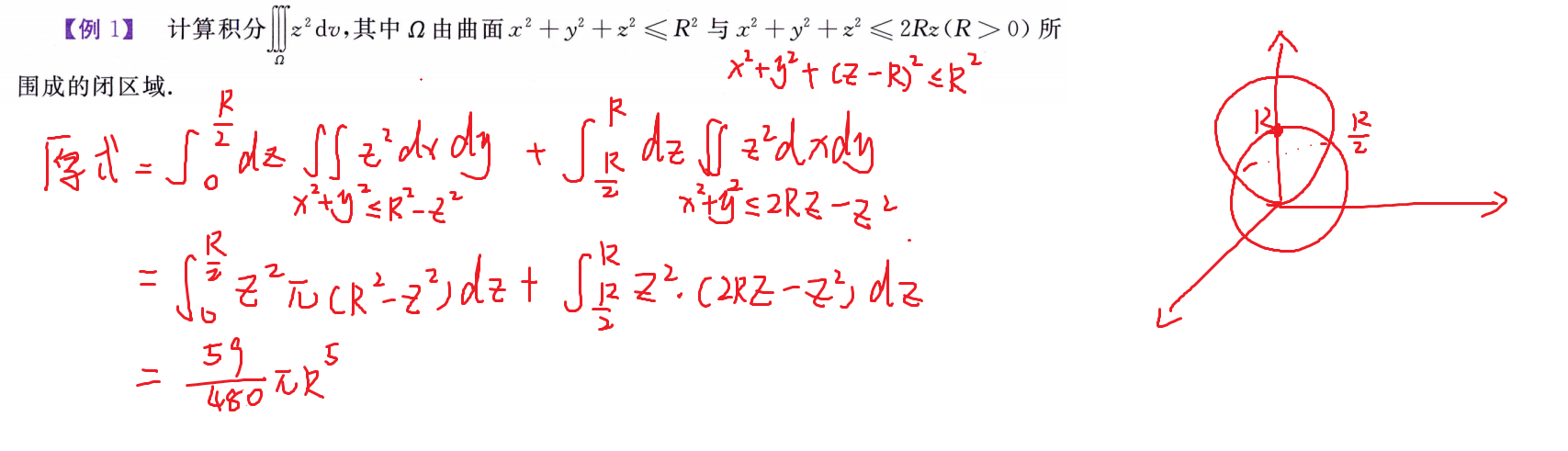
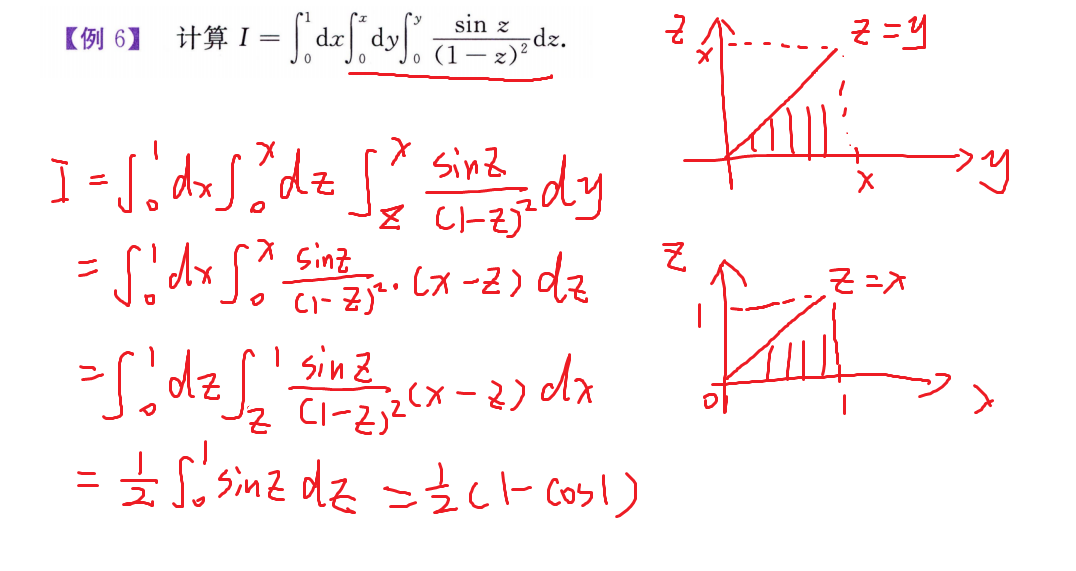
对弧长的线积分计算（第一类）

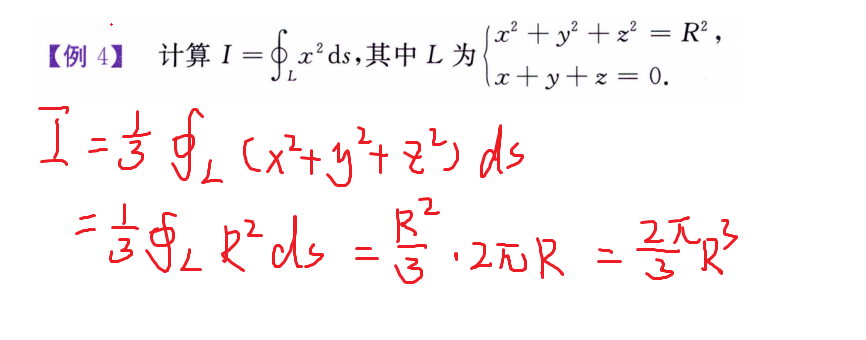
对坐标的线积分计算（第二类）

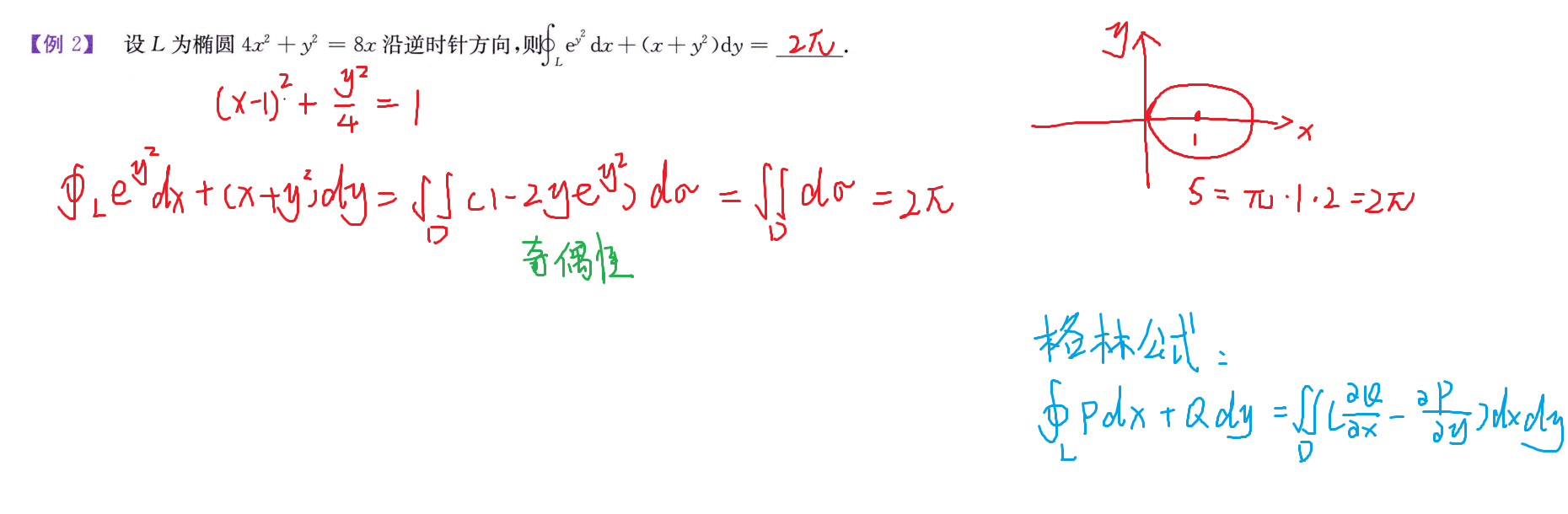
对面积的面积分计算（第一类）

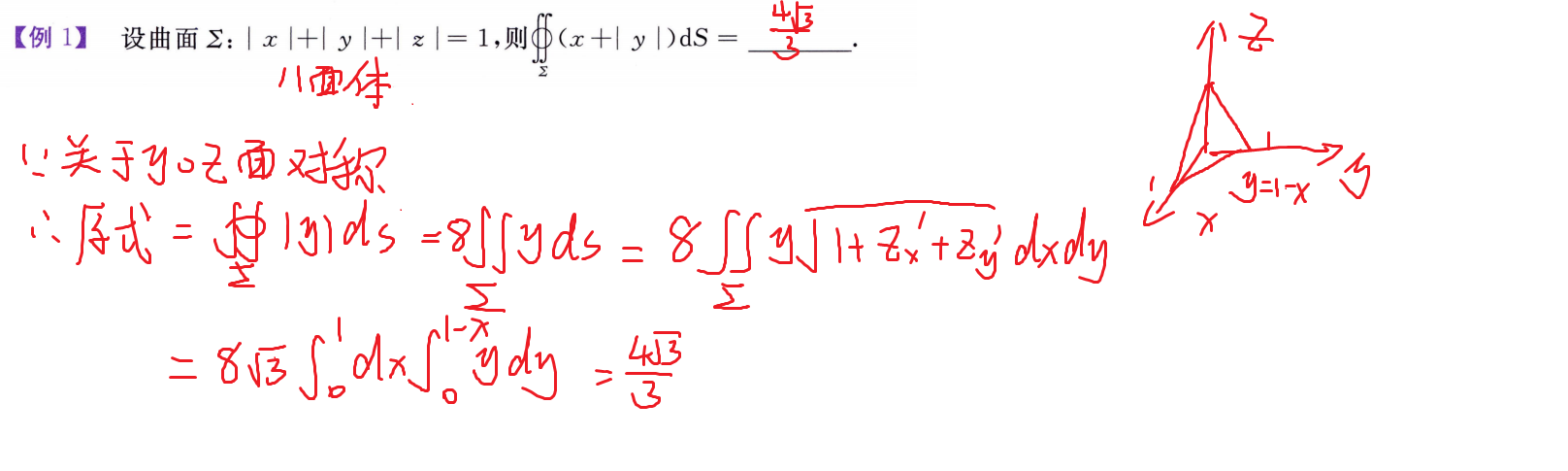
对坐标的面积分计算（第二类）

强化例题（多元积分应用）

考点

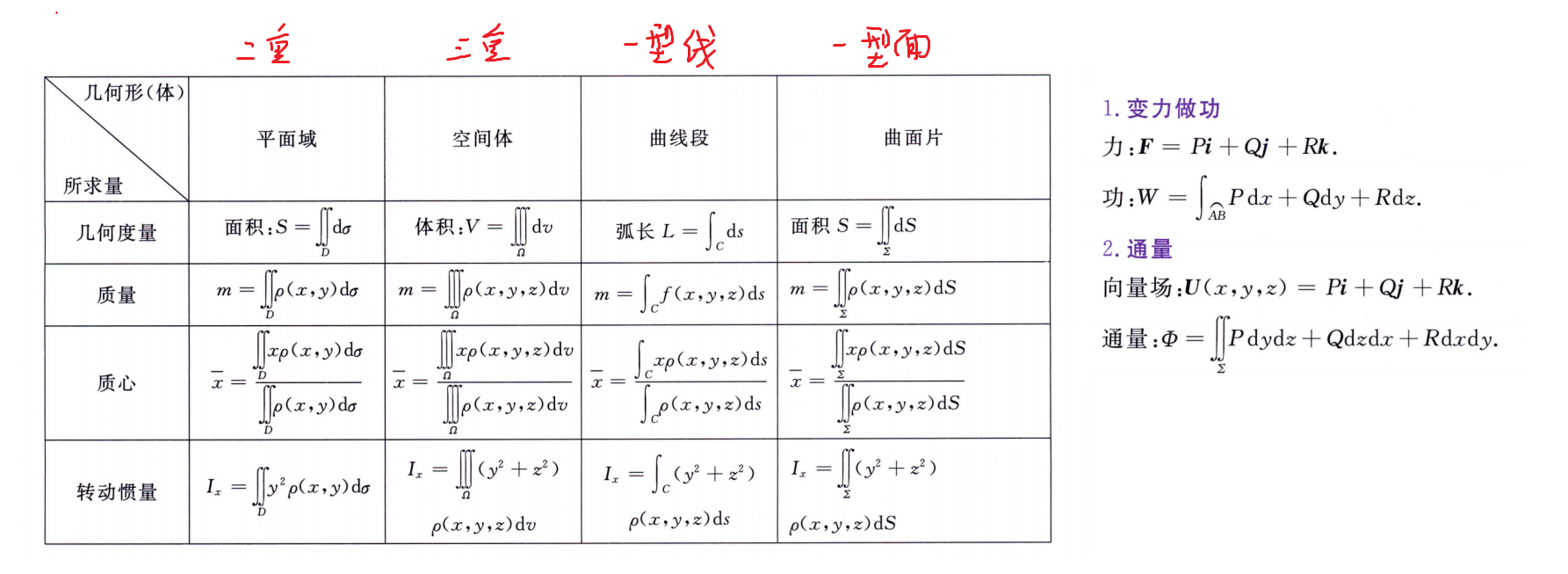
例题