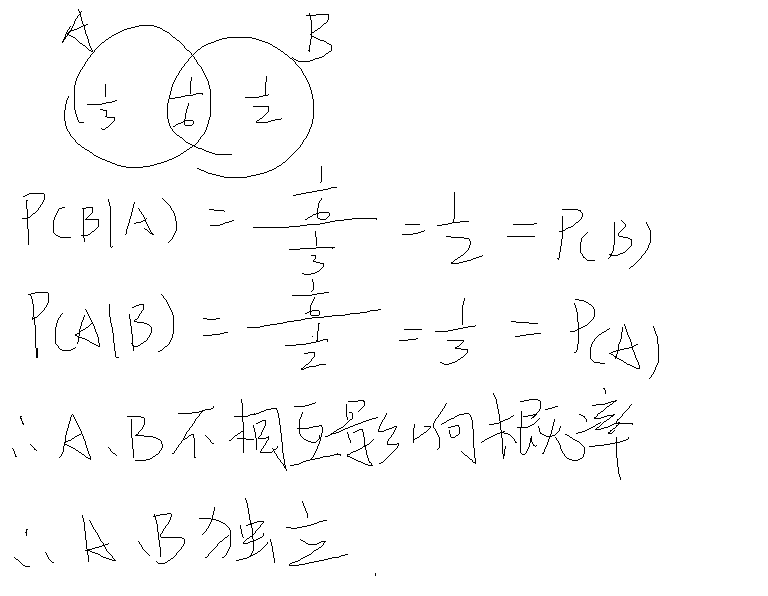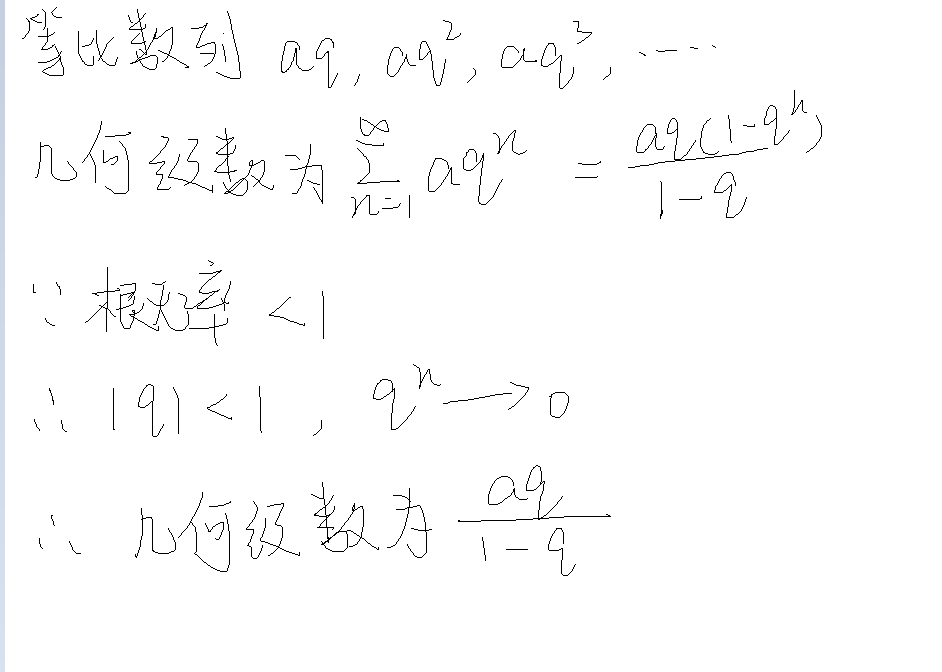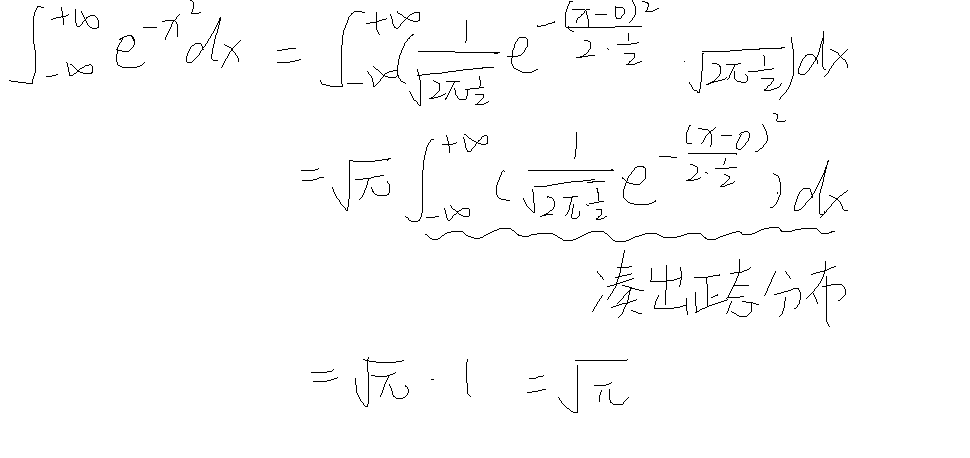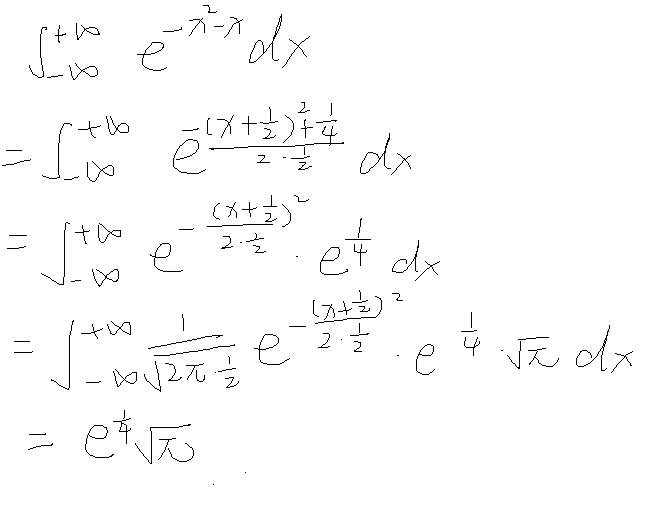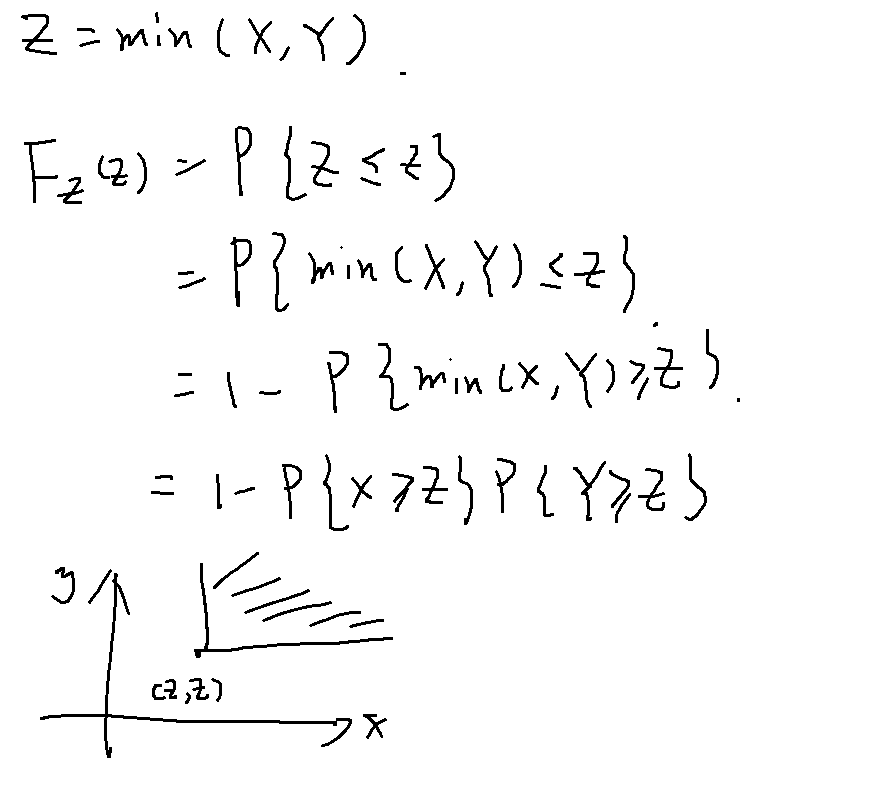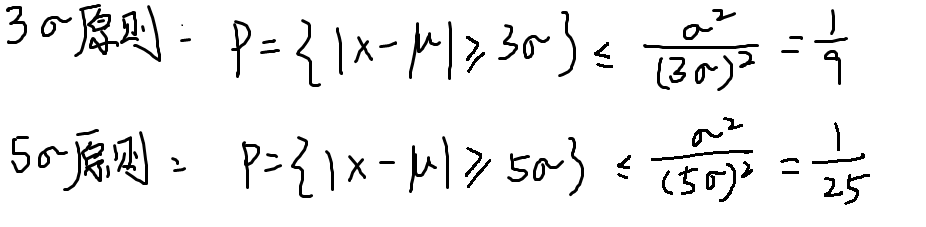概率论基础

事件和概率

事件可以算出概率，概率推不出事件

概念

样本空间：随机试验的所有可能结果组成的集合

样本点：随机试验的每个结果

随机事件：包含若干样本点的集合，某个样本点的出现叫做事件发生

排列和组合：

古典概型

1. 样本空间只包含有限个样本点
2. 每个样本点发生的概率相同

P(A) = A中包含的基础事件数量 / 基础事件的总数

例题

注意点：

1. 分类讨论用加法、分步进行用乘法
2. 有些问题用1减去对立事件发生的概率更好做

实际推断原理：概率很小的事件再一次实验中几乎不发生，如果在一次实验中发生了，有理由怀疑假设的正确性

几何概型

1. 样本空间只包含无限个样本点
2. 每个样本点发生的概率都是“相同的”，为0

P(A) = A的测度（长度、体积、面积） / 总的测度

例题

事件

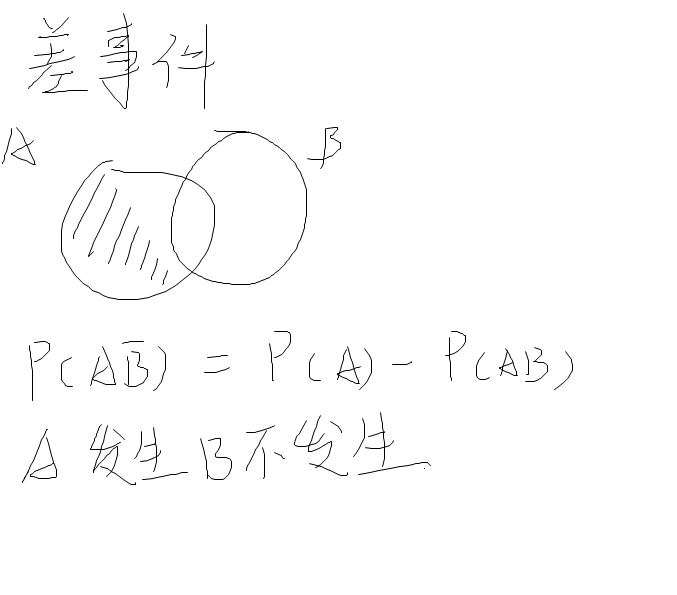
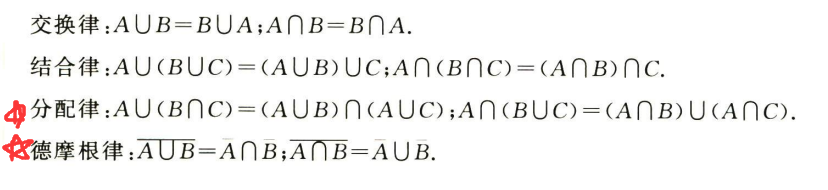
互斥关系：没有交集，AB = ∅，P(AB) = 0

对立关系：AB = ∅，A∪B = Ω

例题

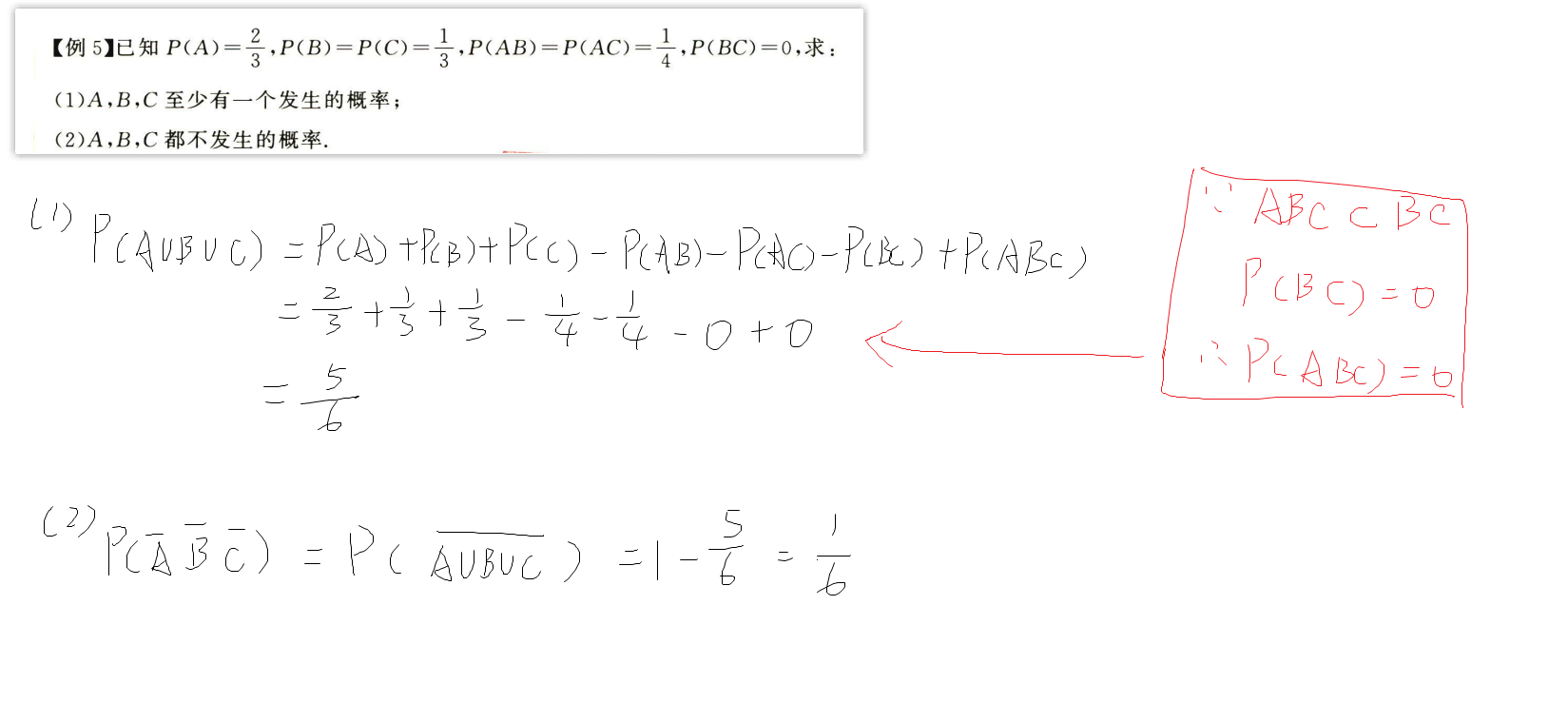
条件概率

P(B|A) = P(AB) / P(A)，在事件A发生的条件下事件B发生的概率

乘法公式：P(AB) = P(B|A)P(A)

例题

全概率公式和贝叶斯公式

全概率公式：

A发生的概率等于在各种条件下A发生的概率之和

P(A) = P(AB1) + P(AB2) + P(AB3) + … + P(ABn)

= P(A | B1)P(B1) + P(A | B2)P(B2) + P(A | B3)P(B3) + … + P(A | Bn)P(Bn)

贝叶斯公式：

在A发生的条件下，是某个条件的概率

P(Bi | A) = P(A | Bi)P(Bi) / P(A)

例题

独立性

A、B事件相互独立，

则 P(B|A) = P(AB) / P(A) = P(B)

∴ P(AB) = P(A)P(B)

因此，一个事件的发生与否不改变另一个事件发生的概率

注意：

• 只要不影响概率就是相互独立的，两件事不一定毫无关系
• P(A)>0，P(B)>0，如果A、B互斥，那么A发生B就不发生，A、B不相互独立
• A包含B，则A、B不相互独立
• 用P(AB) = P(A)P(B)判断独立性，不要凭感觉
• 三个事件相互独立，则两两也独立

例题

一维随机变量及其分布

随机变量

随机试验结果数值化

分类：

1. 离散型
2. 连续性
3. 混合型

离散型随机变量

常见离散型分布

1. (0-1)分布

   X~B(1, 概率)

   

2. 二项分布

   X~B(重复次数, 概率)

   

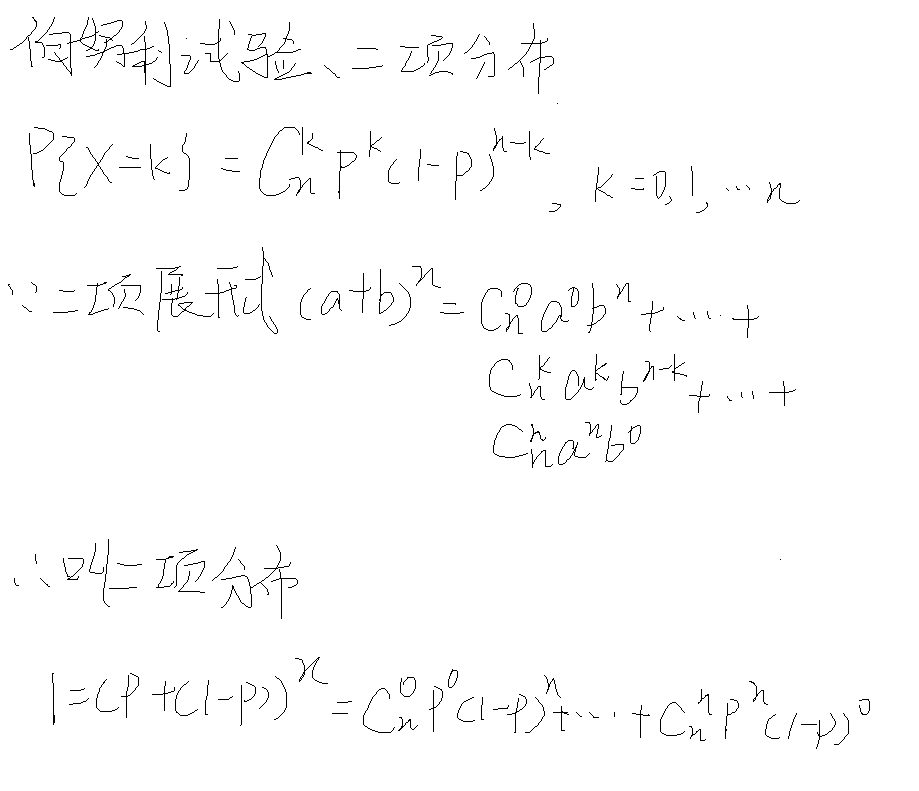
3. 几何分布

   X~G(概率)

   

4. 负二项分布

   

几何级数公式推导↓

5. 泊松分布

   k可以看成粒子流在单位时间内通过的粒子个数，只能是整数

   X~π(λ)

   

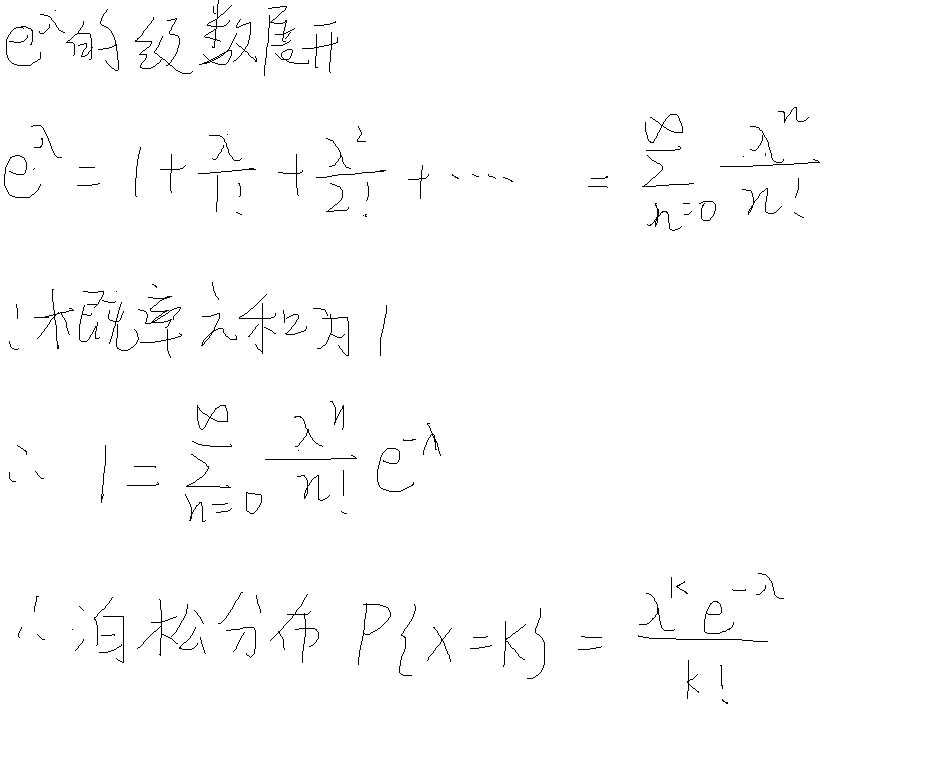
例题

分布函数

X是随机变量，x是任意实数，F(x) = P{X <= x}，称为X的分布函数

用于计算区间上的概率之和

基本性质：

1. F(x) 是一个单调不减的函数
2. 规范性：F(-∞) = 0，F(+∞) = 1
3. F(x + 0) = F(x)，即右连续

例题

连续型随机变量

概率密度：用密度来表示这个点的概率

1. P{X = x} = f(x)dx
2. ∫(+∞, -∞) f(x) = 1
3. f(x) >= 0，X的取值范围为f(x) > 0的区域
4. 分布函数：F(x) = P{X <= x} = ∫(x, -∞) f(t)dt。F’(x) = f(x),不考虑不可导点
5. F(x)连续，因为一个点的概率为0

分类：

1. 均匀分布
2. 指数分布
3. 正态分布

均匀分布

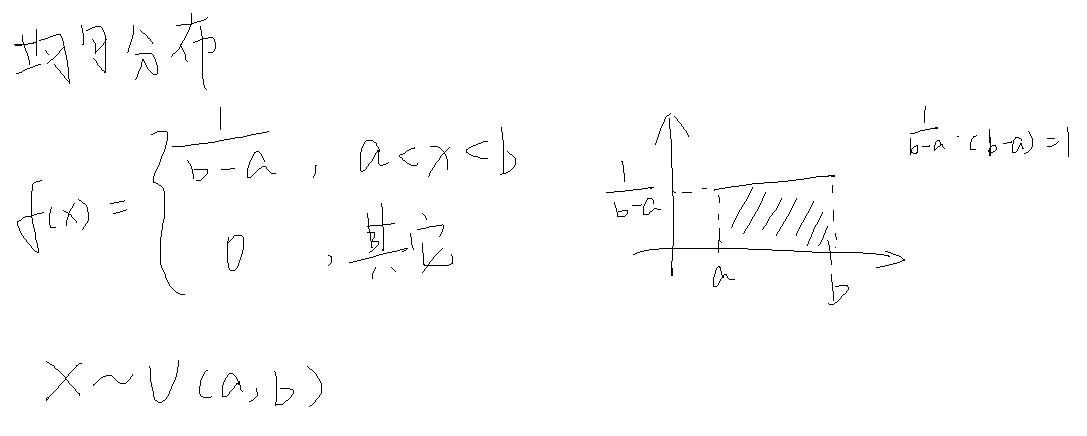
指数分布

λ > 0

X~E(λ)

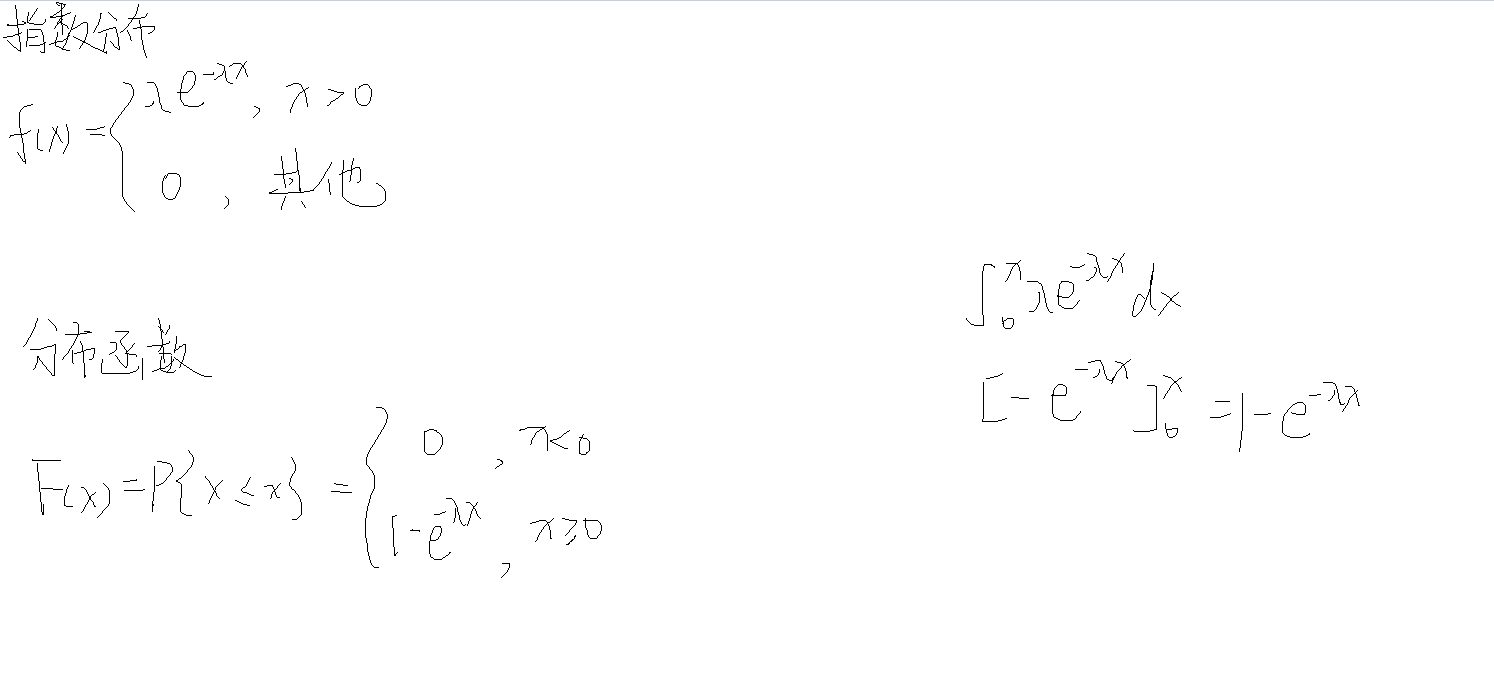
例题

正态分布

利用正态分布计算反常积分

例题

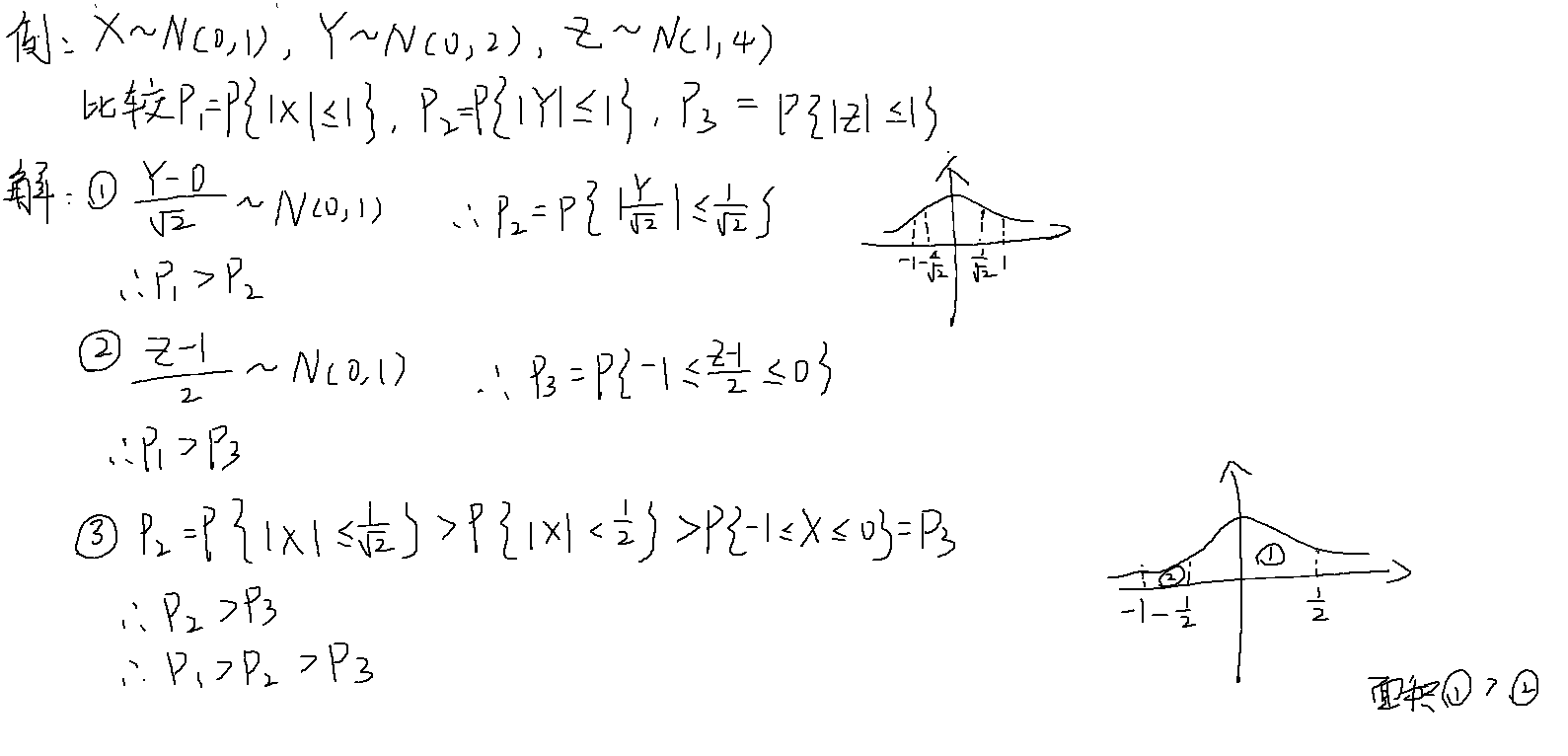
二维随机变量及其分布

离散型

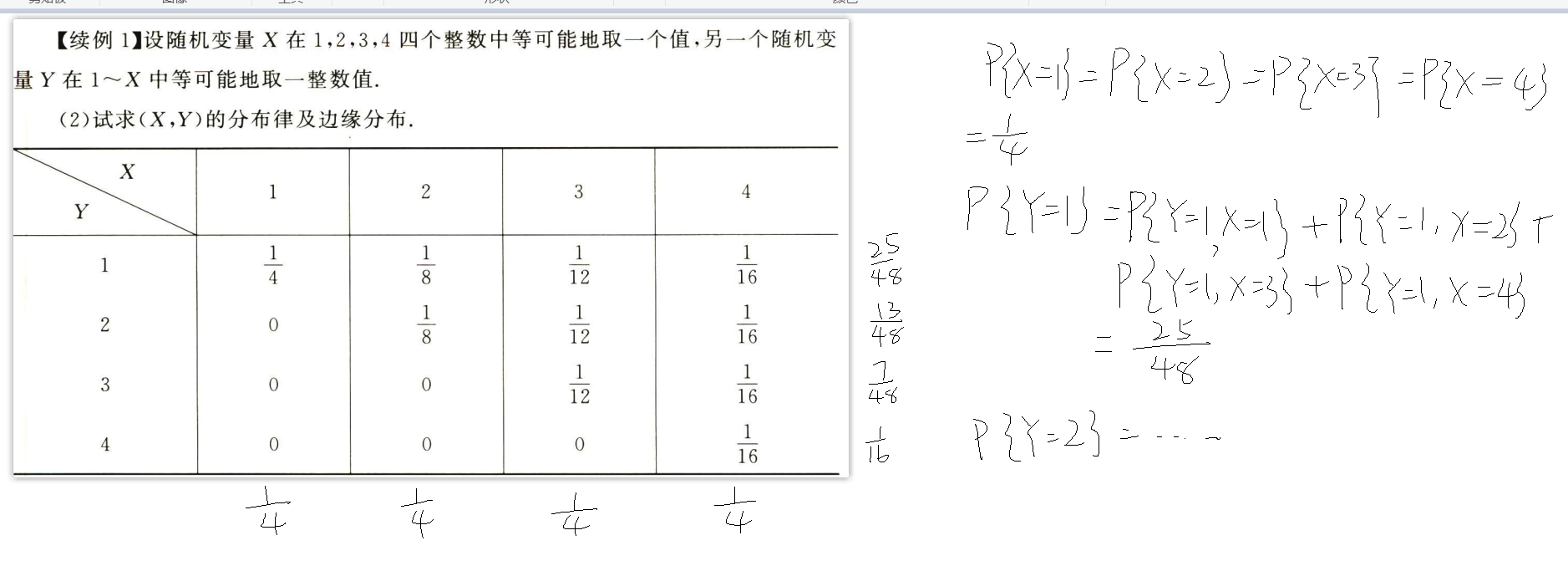
分布律

例题

分布函数

1. 单调不减
2. 右连续
3. 规范型
4. 概率>=0

连续型

概率密度

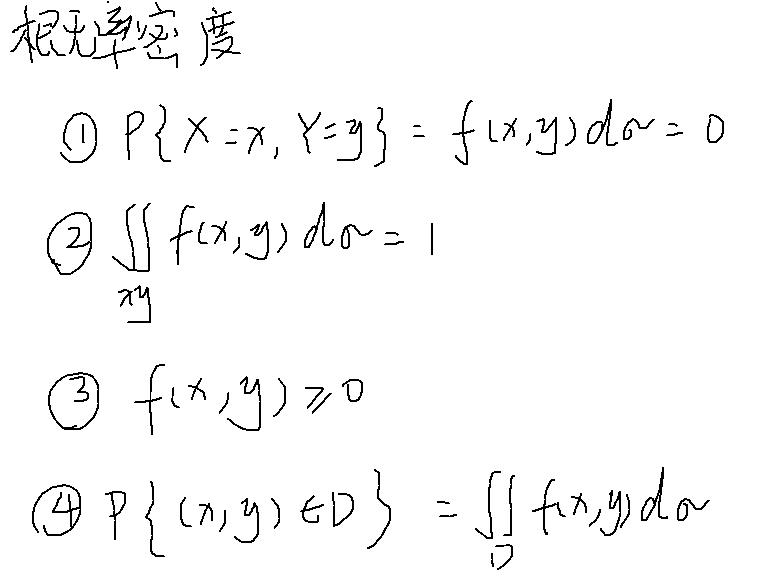
分布函数

例题

二维正态分布

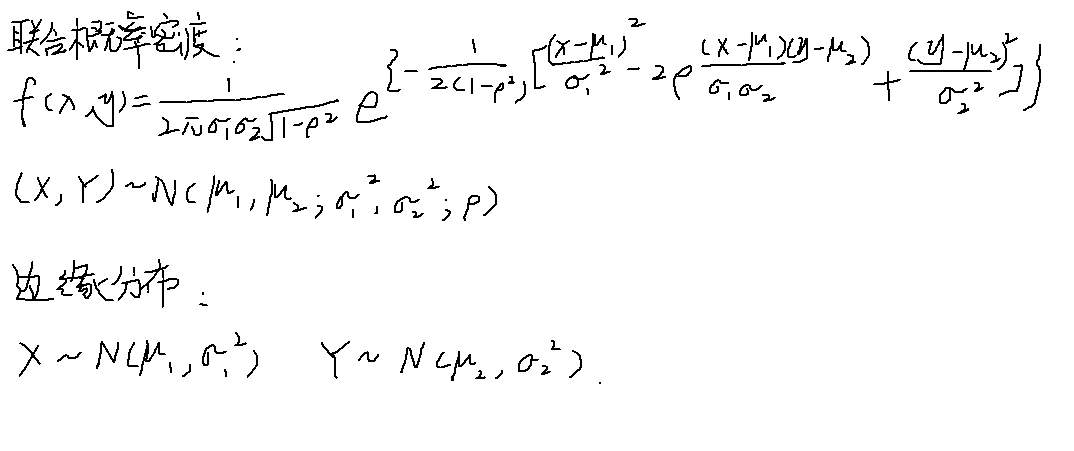
边缘分布

二维随机变量里面只研究一个随机变量

离散型

连续型

做题时一定要画图

条件分布

离散型

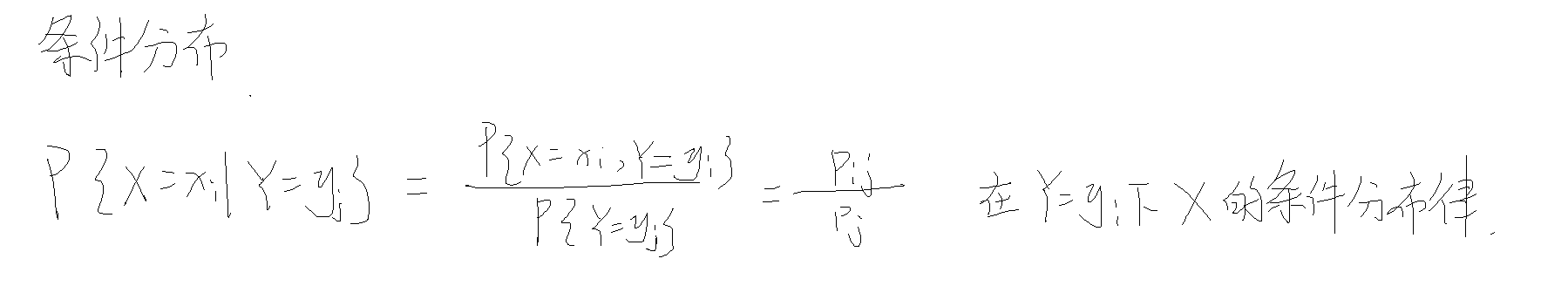
连续型

独立性

1. 连续型判断独立性：概率密度f(x, y) = fX(x)fY(y)
2. 离散型判断独立性：同时发生的概率为各自发生概率的乘积P{X = xi, Y = yj} = P{X = xi}P{Y = yj}

例题

随机变量函数

一维例题

:star:

分布函数法，求导得概率密度

二维例题

如果题目中Z = max(X, Y)或Z = min(X, Y)的情况时

数字特征

期望

期望也就是理论平均值

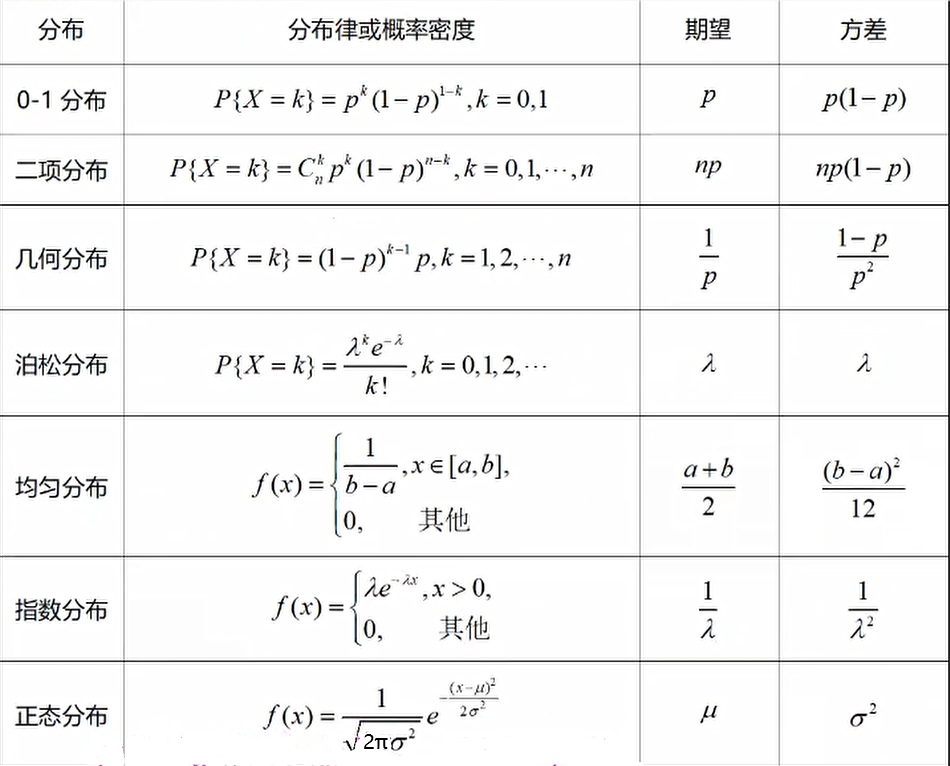
常见分布的期望

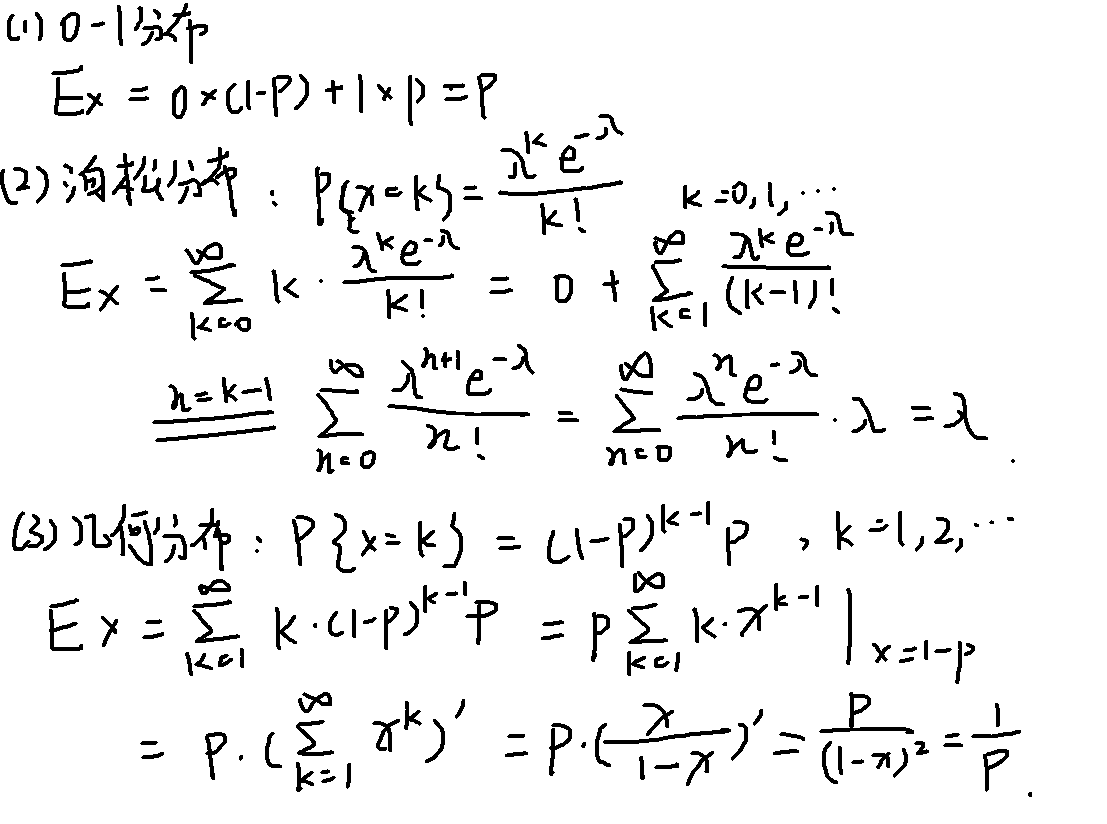
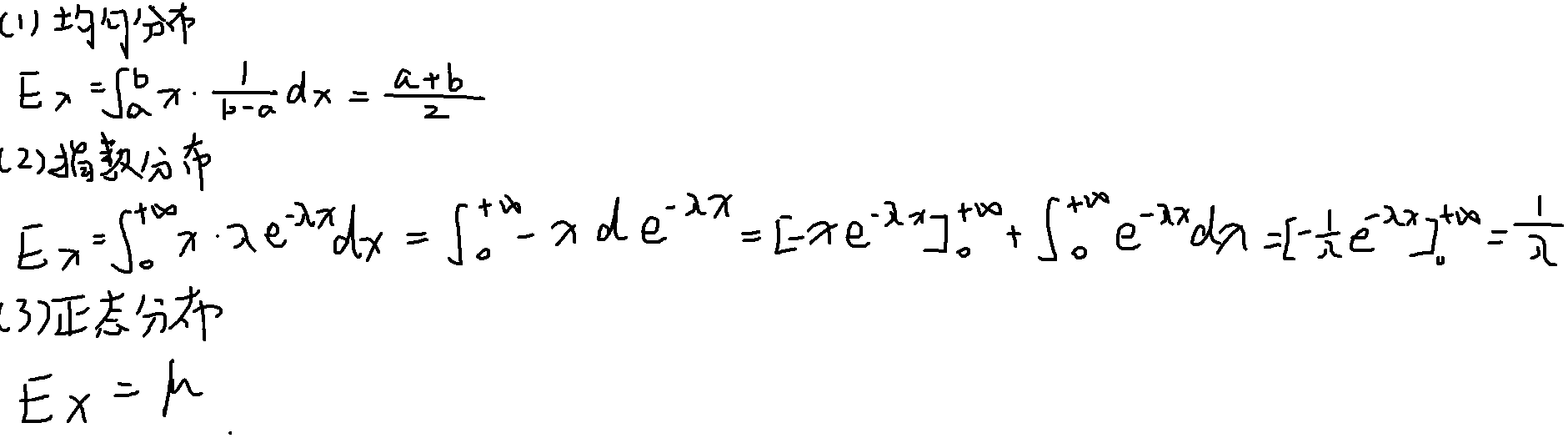
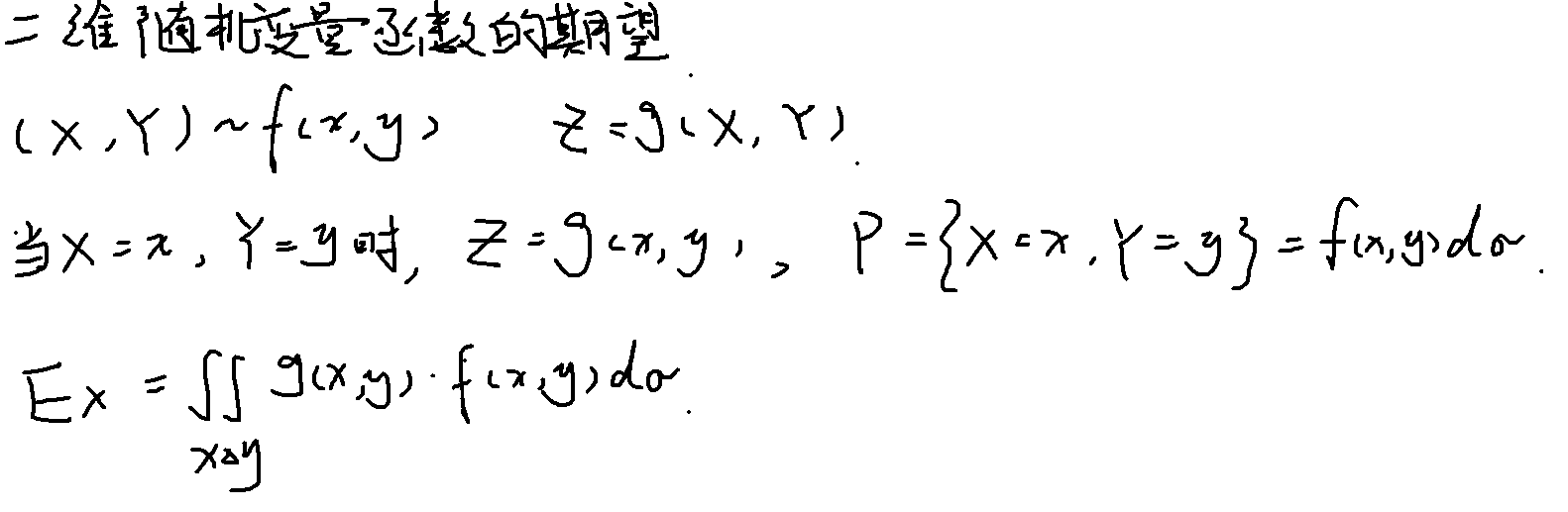
性质

1. 设C是常数，则有E(C) = C
2. X是随机变量，C是常数，则E(CX) = CE(X)
3. X、Y是随机变量，则E(X+Y) = E(X) + E(Y)
4. X、Y是随机变量，且相互独立，则有E(XY) = E(X)E(Y)

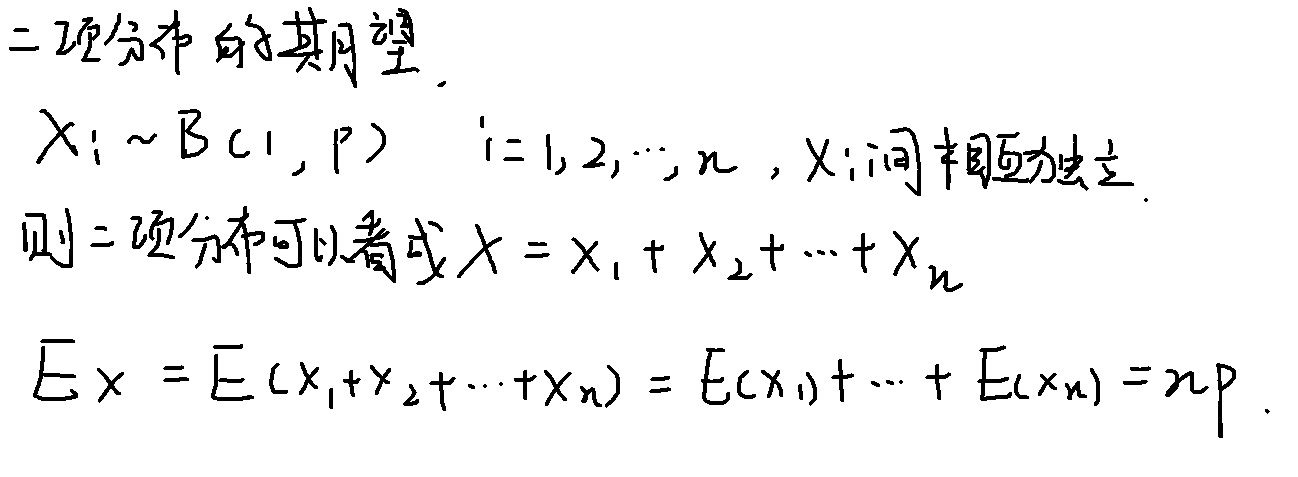
例题

方差

描述了随机变量在期望上下波动的程度

方差为偏离程度的平均值(期望)

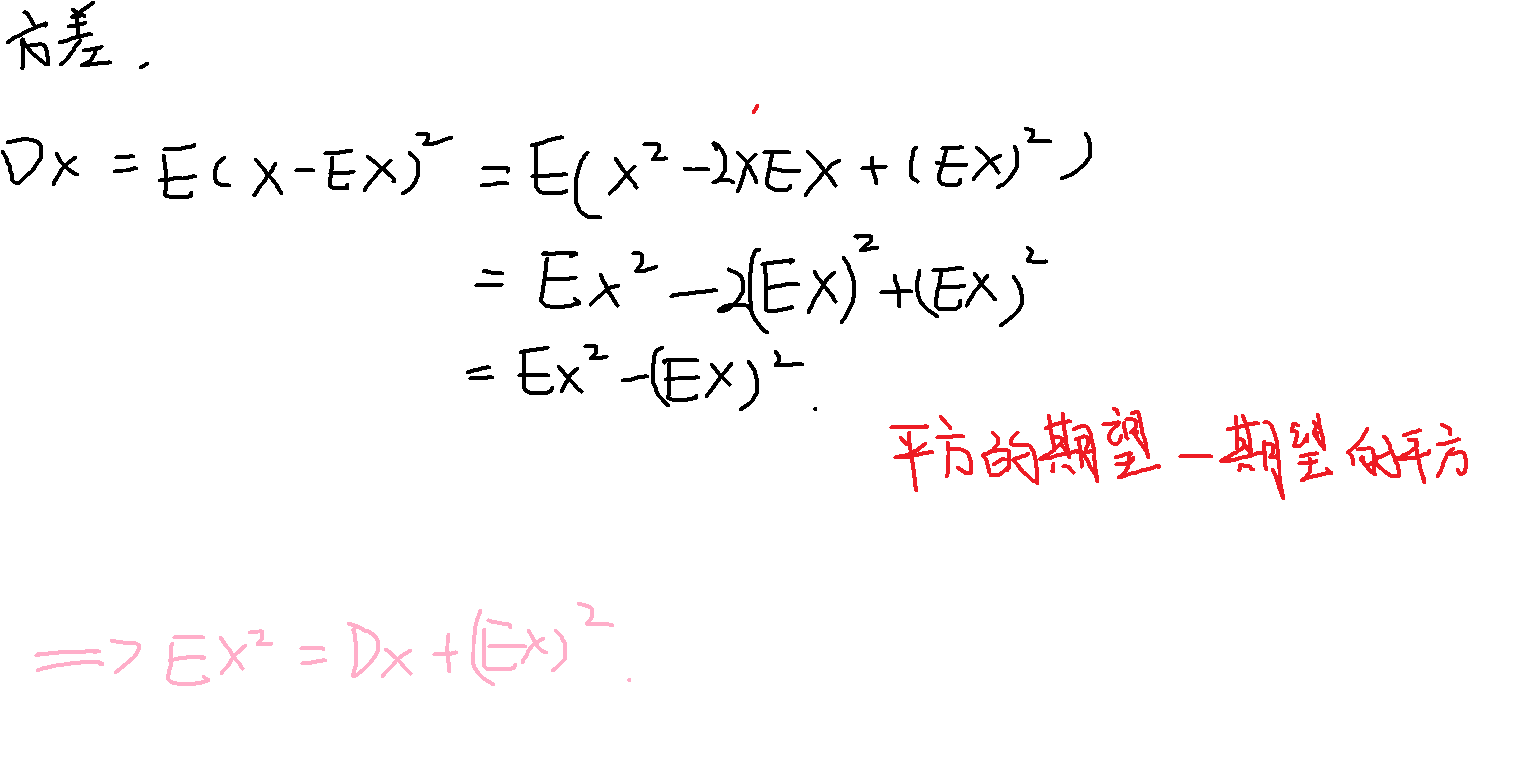
性质

1. C是常数，D(C) = 0

2. C是常数，D(CX) = C²D(X)，D(X + C) = D(X)

3. D(X+Y) = D(X) + D(Y) + 2E{ (X - E(X)(Y - E(Y))) }

   若X、Y相互独立，则D(X+Y) = D(X) + D(Y)

4. D(X) = 0 <==> P{X = E(X)} = 1

常见分布的方差

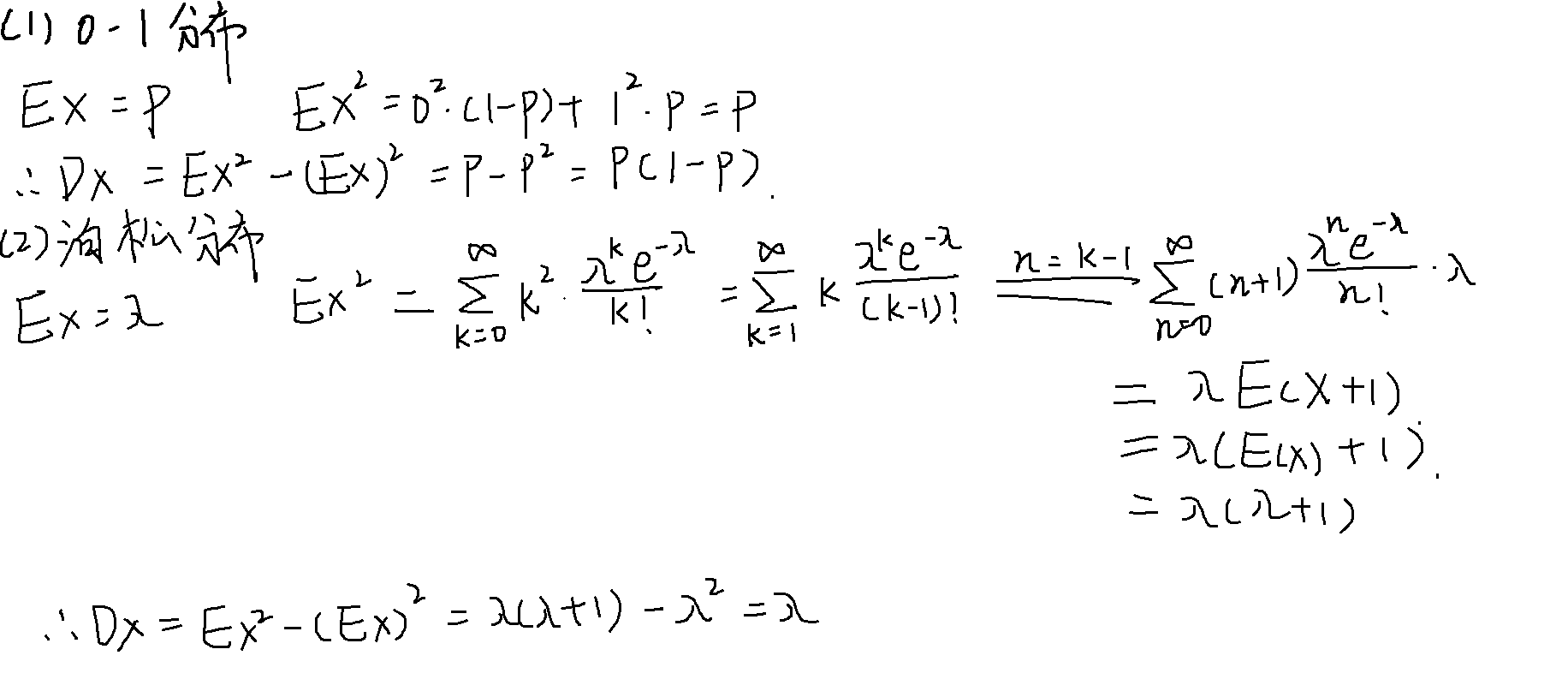
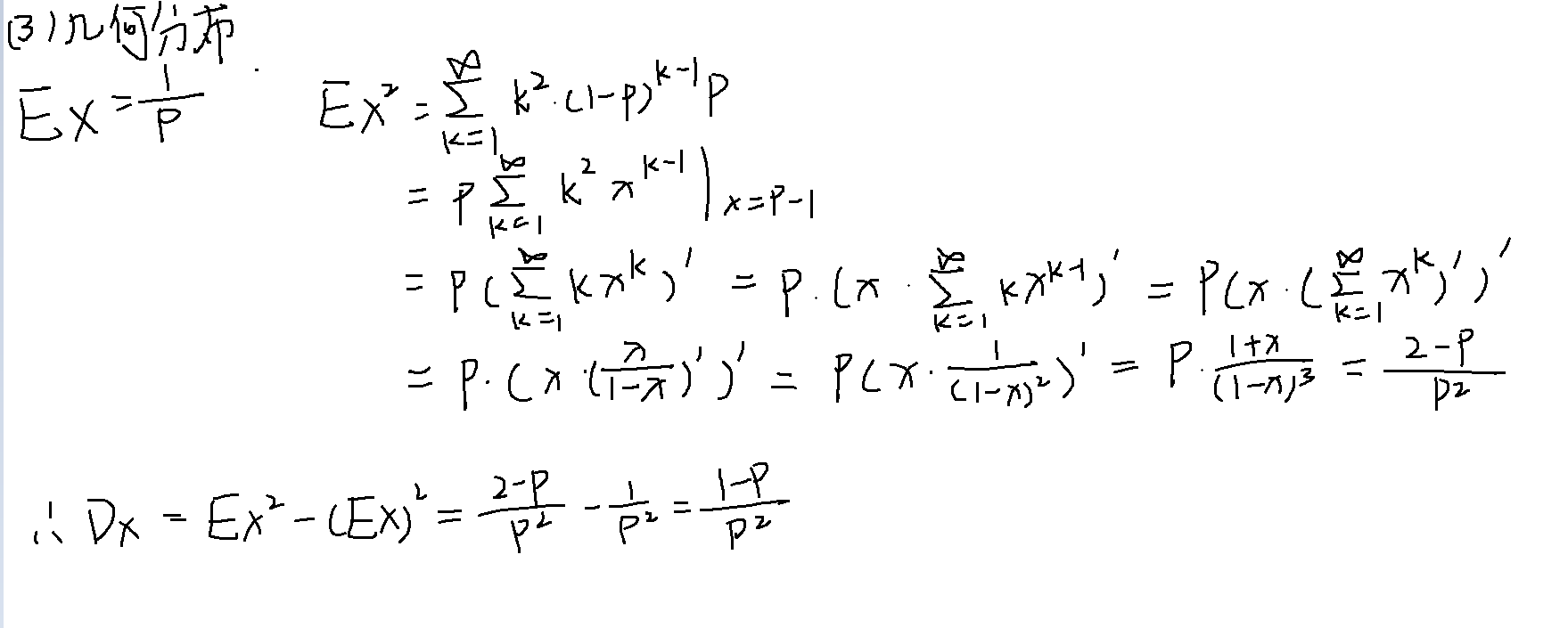
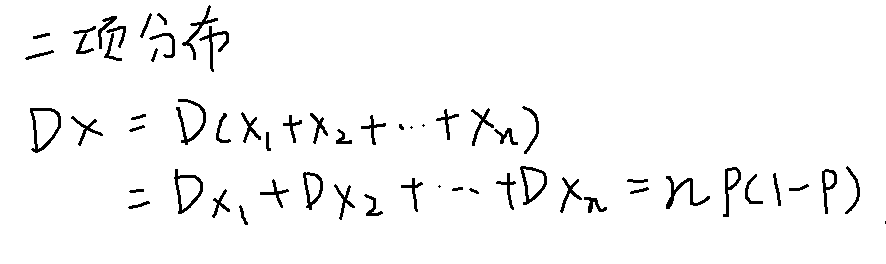
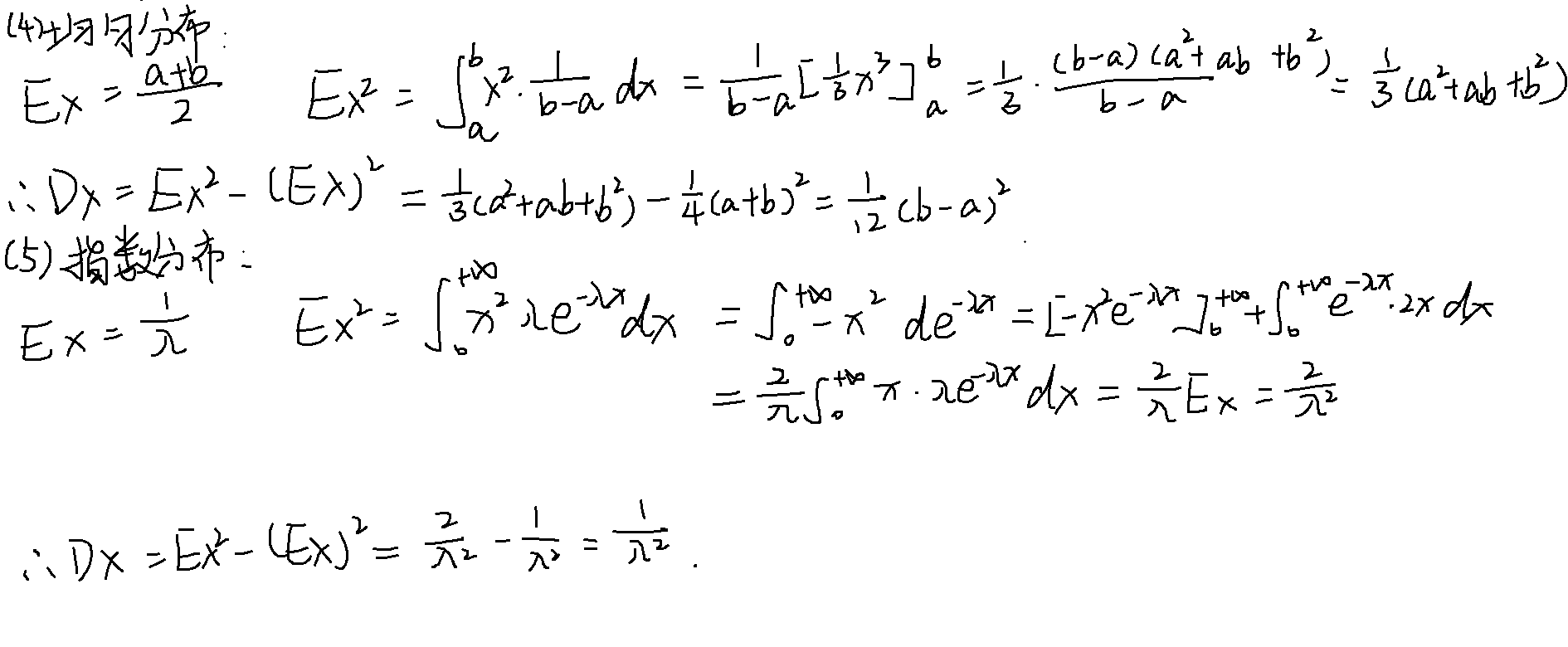
伽马函数

正态分布的方差是σ²

协方差

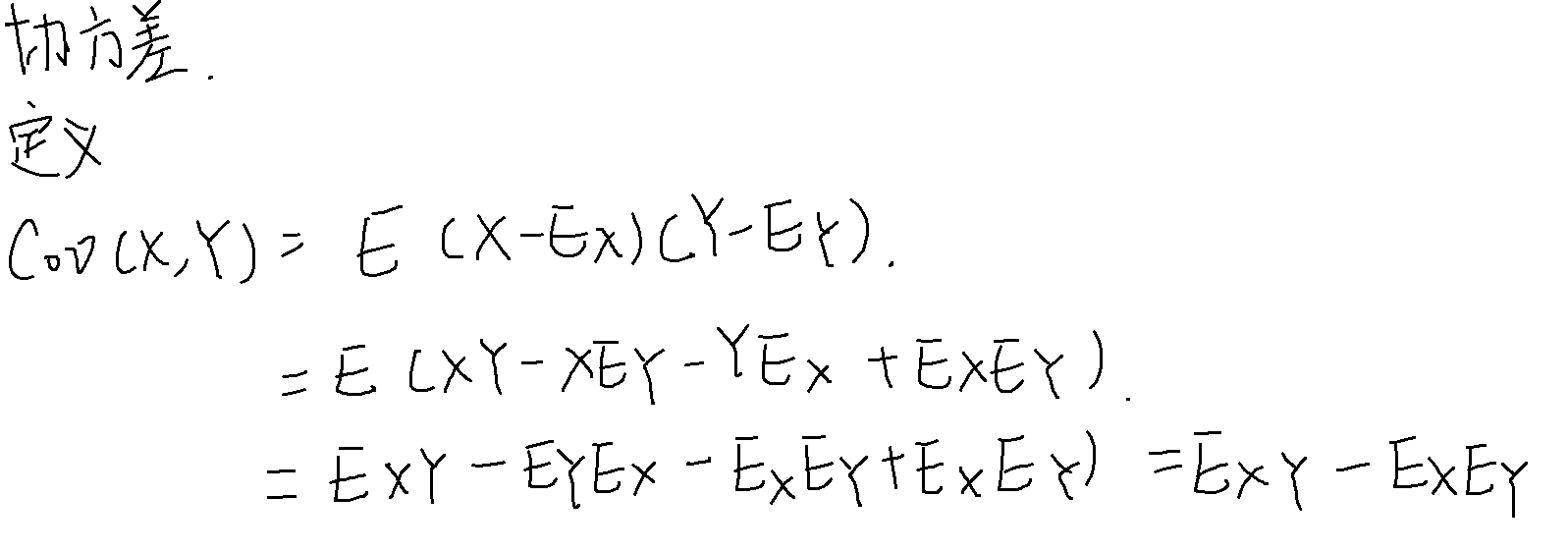
​ 协方差是两个随机变量 X 和 Y 之间线性关系的度量。协方差为正表示 X 和 Y 具有正相关关系，即当 X 增大时，Y 也倾向于增大；协方差为负表示 X 和 Y 具有负相关关系，即当 X 增大时，Y 倾向于减小

性质

1. a，b为常数，Cov(aX, bY) = ab Cov(X, Y)
2. Cov(X1 + X2, Y) = Cov(X1, Y) + Cov(X2, Y)
3. 若X、Y相互独立，则Cov(X, Y) = 0
4. C为常数，Cov(X, C) = 0
5. Cov(X, X) = E(X - EX)(X - EX) = DX

例题

相关系数

相当于将协方差标准化，使取值范围在[-1, 1]之间，都是用于描述两个随机变量的相关性

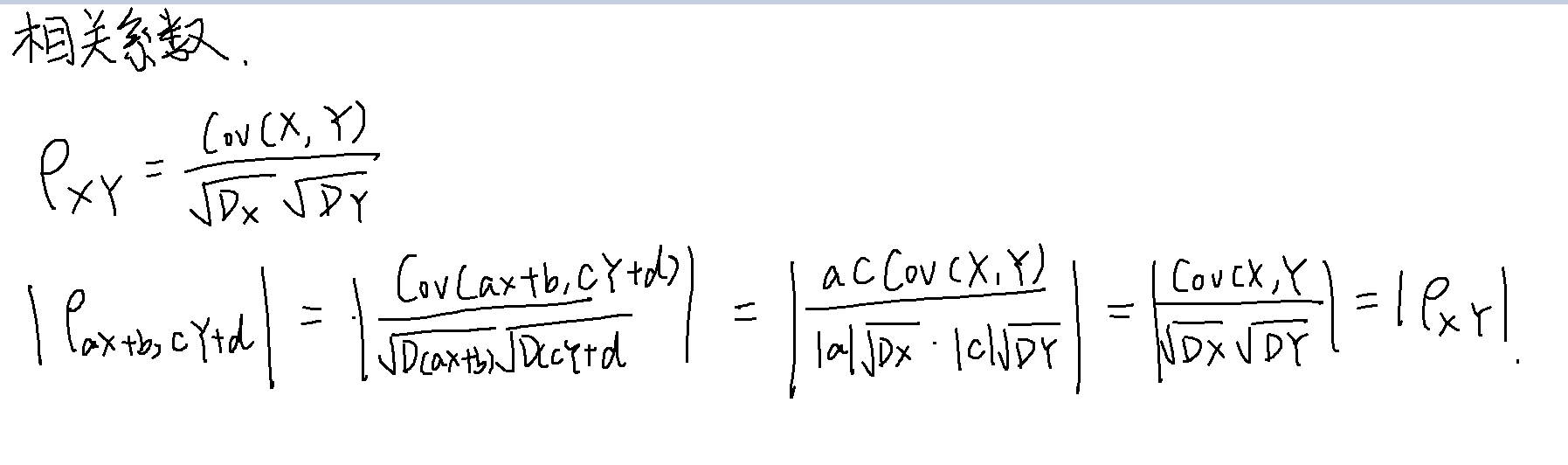
性质

1. |ρXY| <= 1
2. |ρXY| = 1 充要条件是 P{Y = aX + b} = 1
3. 相互独立则ρXY = 0

例题

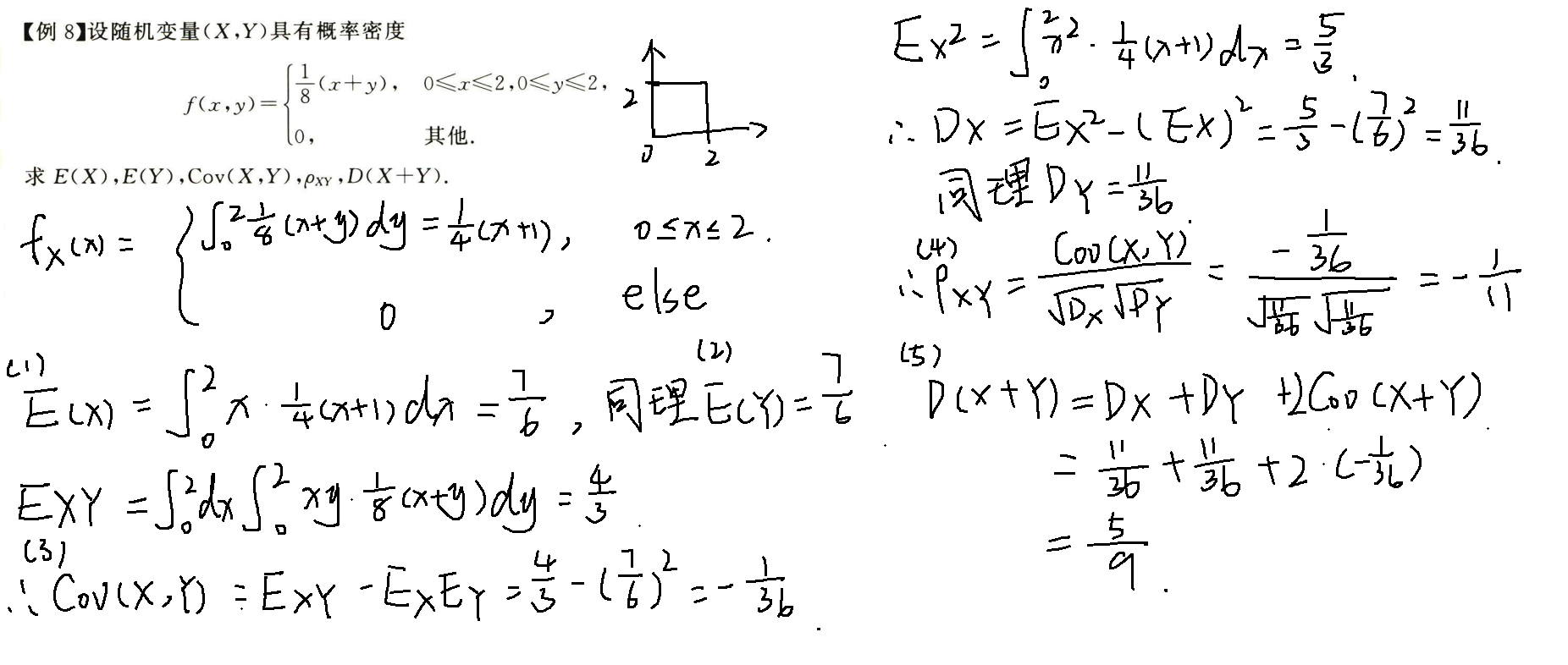
矩

总结和例题

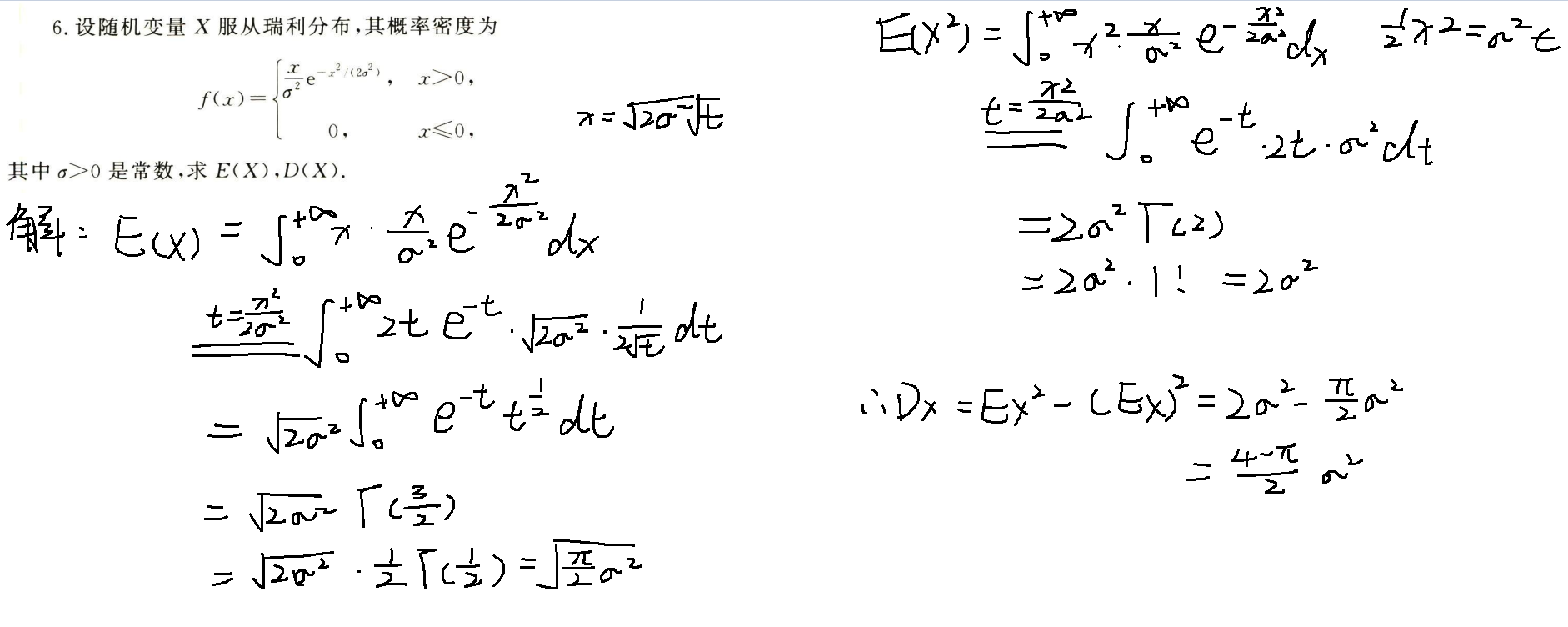
大数定律

切比雪夫不等式

用于描述随机变量与其均值之间的偏离程度

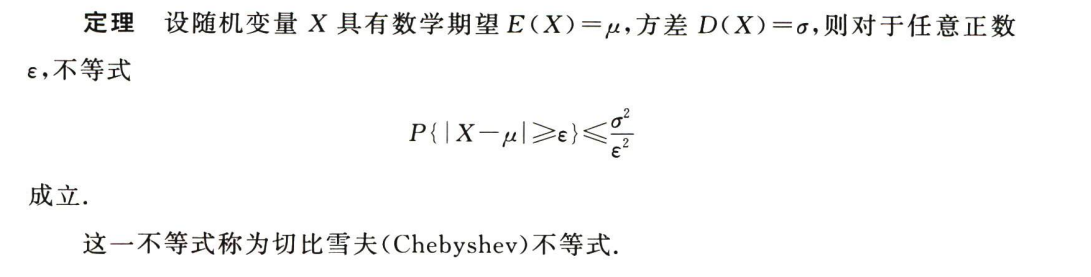
用于去掉异常数据

依概率收敛

大量样本的平均值具有稳定性

大数定理

弱大数定理

伯努利大数定理

切比雪夫大数定律

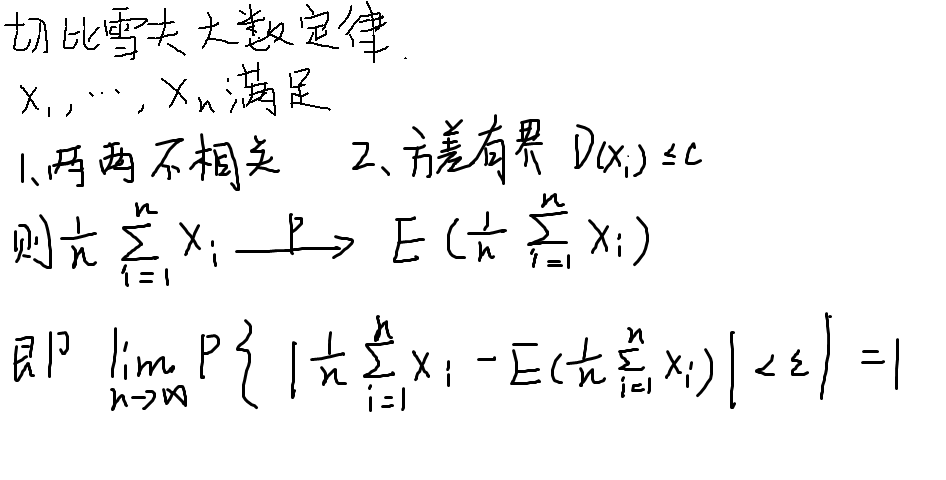
中心极限定理

数理统计基础

统计量

统计量是用来描述和总结一组数据的数值指标。

X1、X2、…、Xn独立同分布，则称为从分布函数F得到的容量为n的简单随机样本

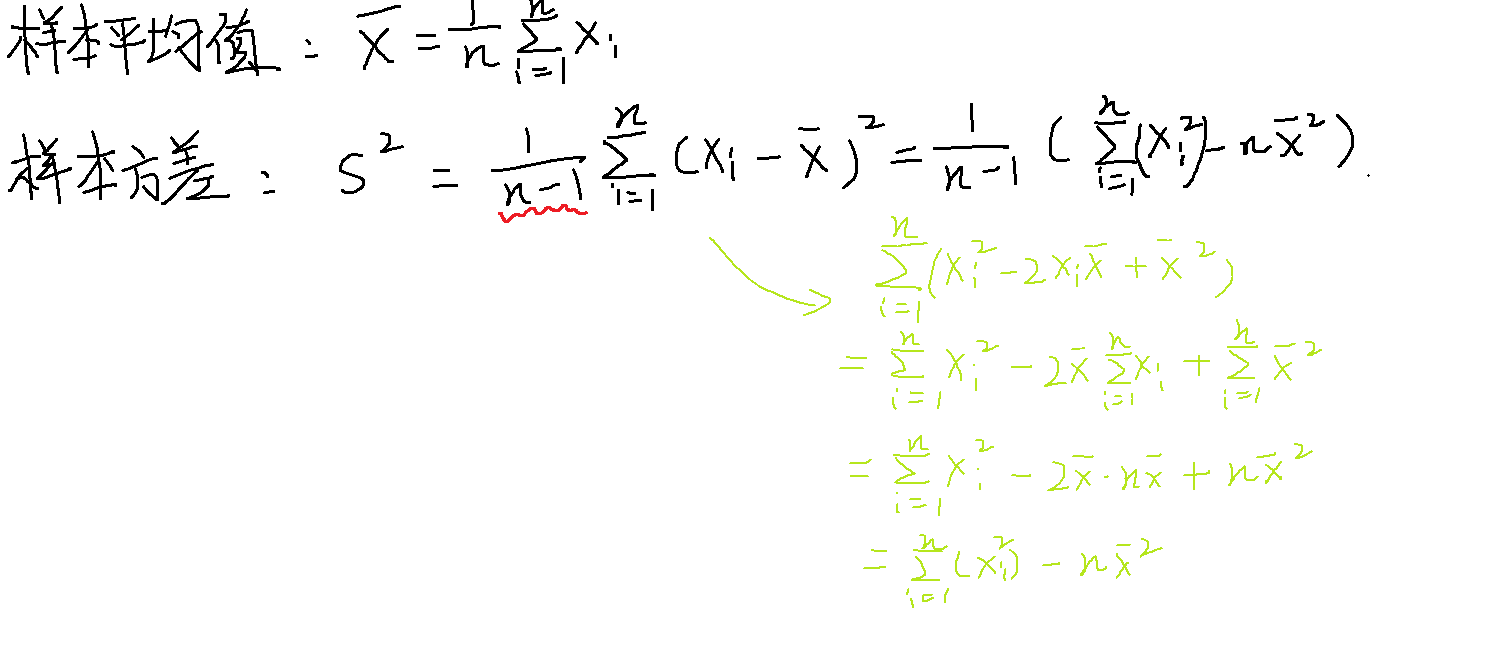
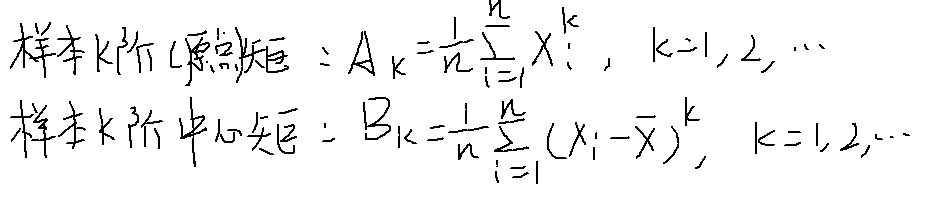
统计量的数字特征

抽样分布

统计量的分布

x²分布

注意是标准正态分布的抽样分布

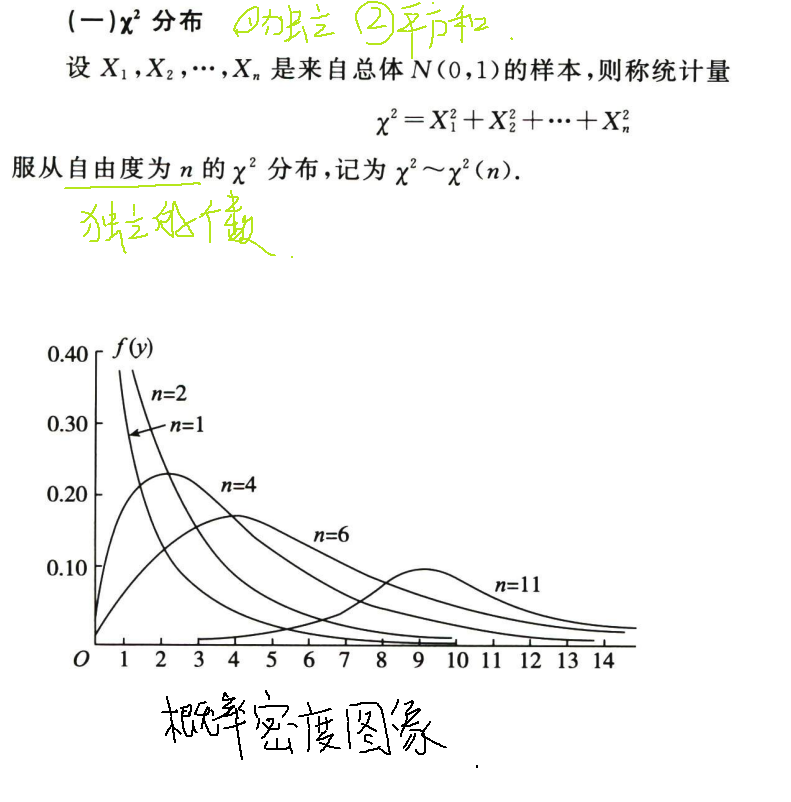
性质

例题

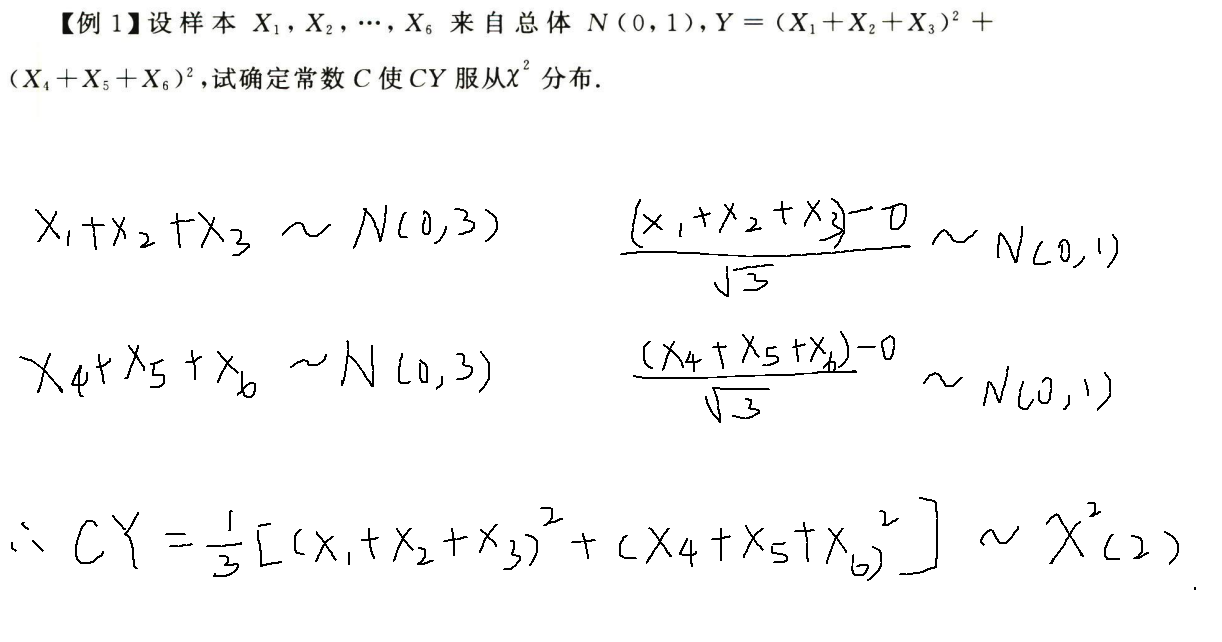
t分布

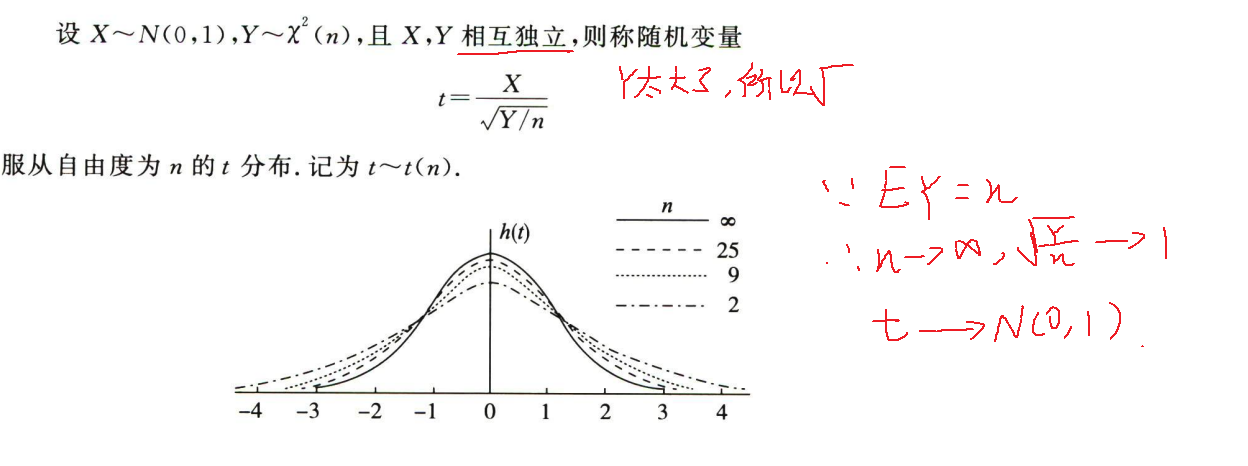
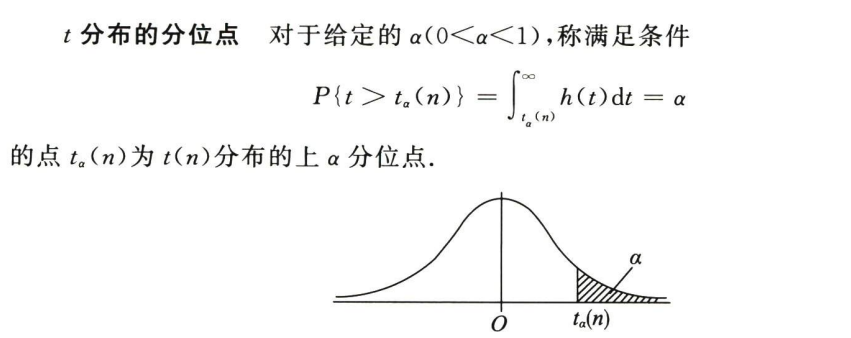
例题

F分布

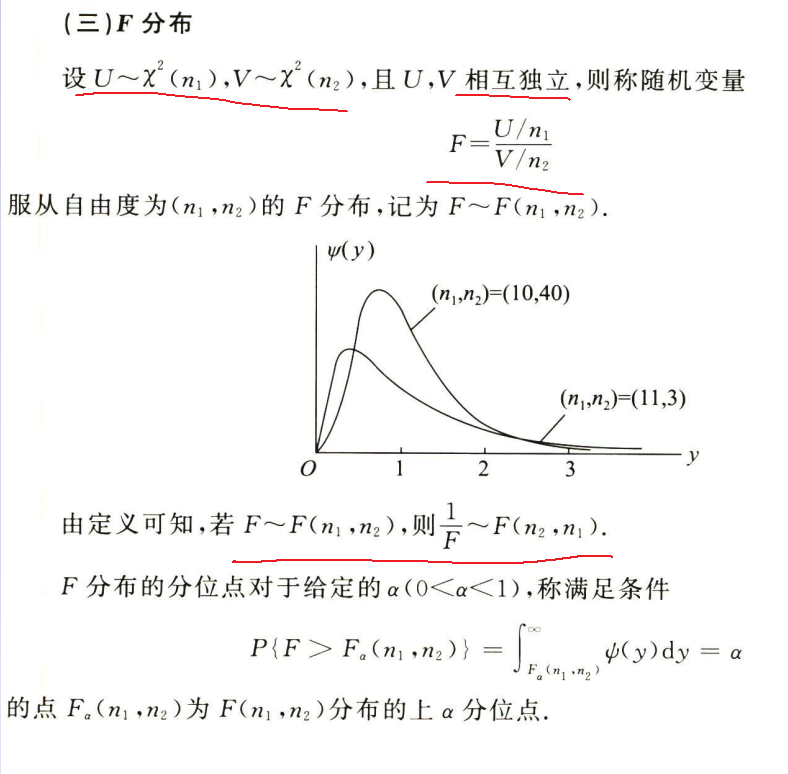
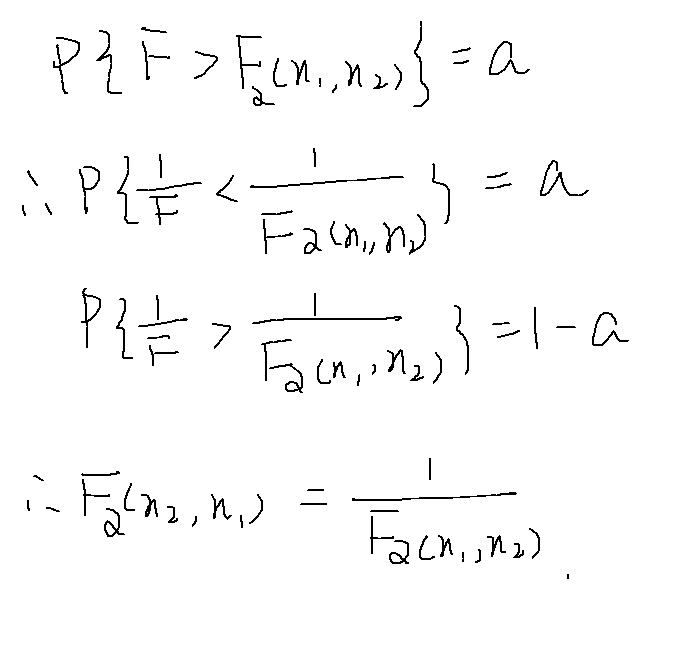
例题

参数估计与假设检验

点估计

X的分布函数已知，但一个或多个参数未知，通过样本来来估计未知参数的值称为参数的点估计问题

矩估计

用样本的原点矩、中心矩来近似整体的期望和方差

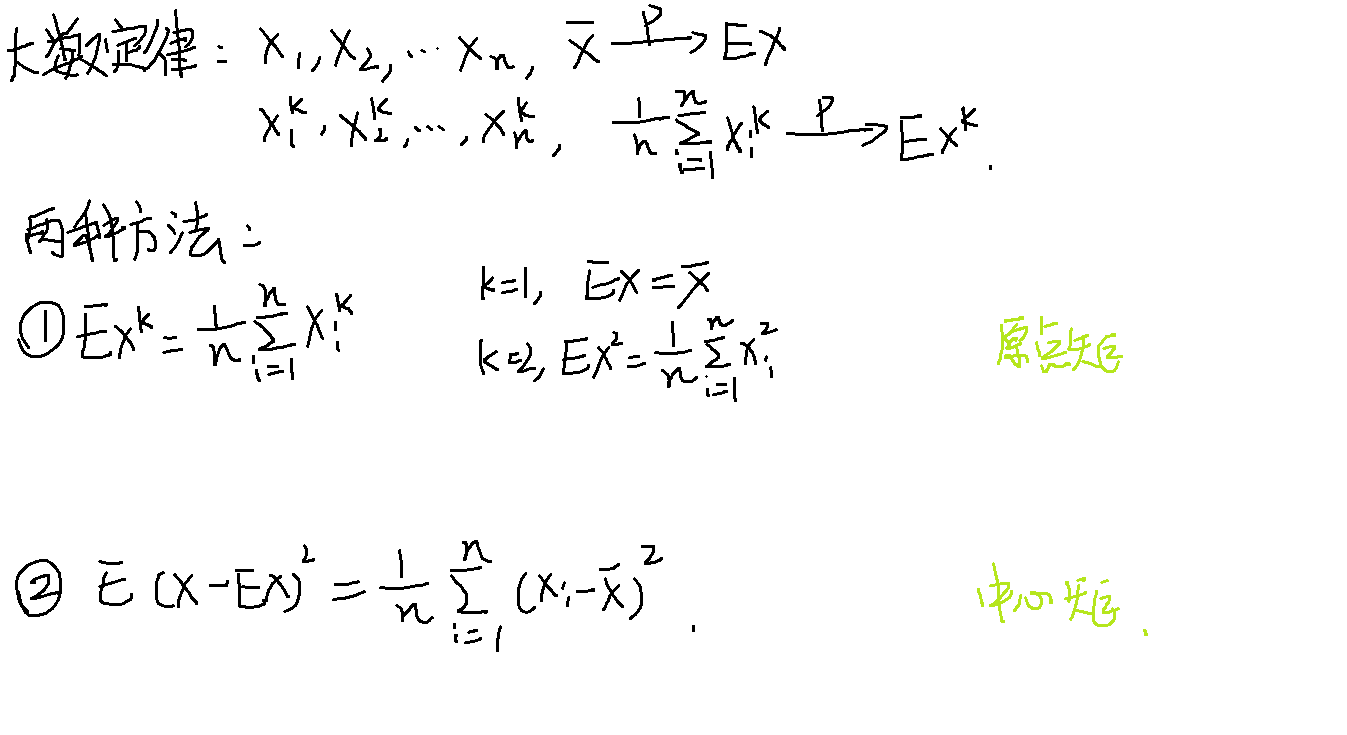
例题

最大似然估计

假设我们有一个参数化的概率分布模型 P(X; θ)，其中X表示观测数据，θ表示需要估计的参数。最大似然估计的目标是找到参数θ的值，使得在给定观测数据X时，数据出现的概率（似然函数）最大。

离散型

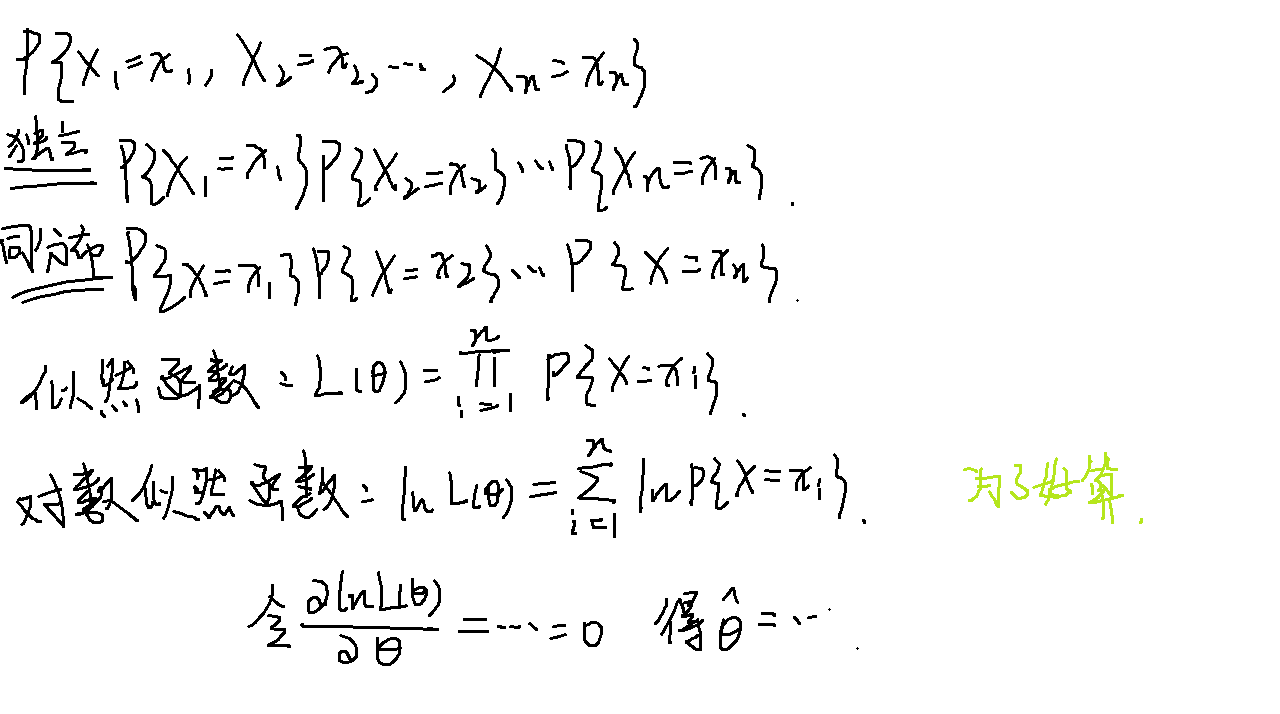
例题

连续型

例题

估计量的评选标准

用来评价哪种估计方法好

无偏性

E(估计值) = 待估参数

有效性

D(θ1) <= D(θ2)，则θ1比θ2有效

一致性（相合性）

例题

区间估计

显著性水平：犯错率(α)

置信度：正确率(1 - α)

置信区间：估计的值所在的区间

区间估计：估计的值在置信区间的概率要等于1 - α

题型

假设检验

对样本的均值进行检验，如果落在拒绝域则认为有问题

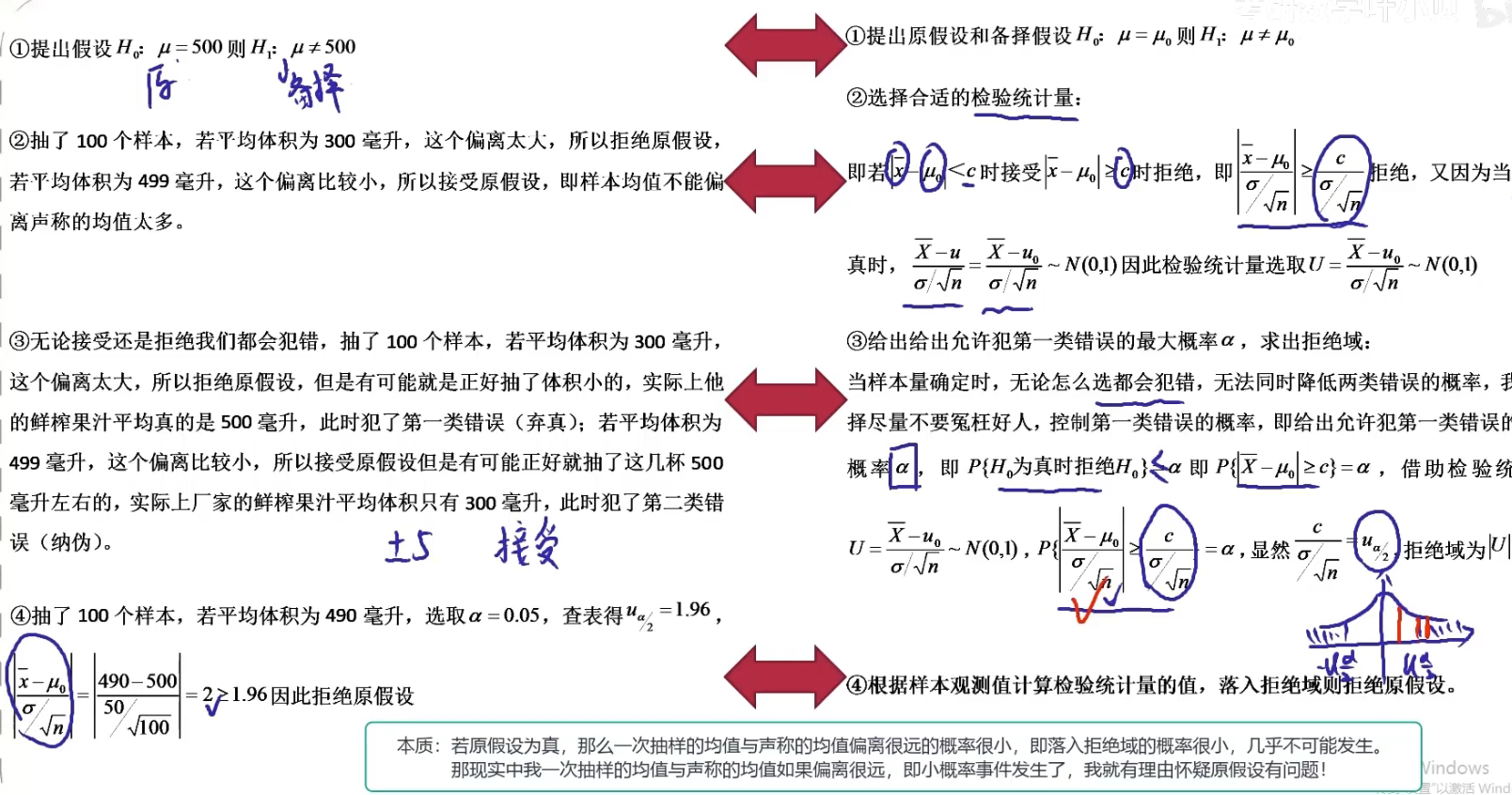
题型

例题