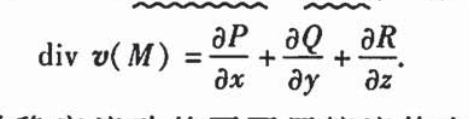高数基础
高数基础
极限
定义
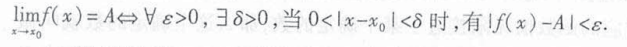
极限运算
- 有限个无穷小的和为无穷小
- 有界函数 x 无穷小 = 无穷小
夹逼定理

重要极限
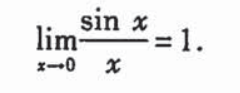
根据夹逼定理证明
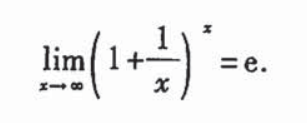
单调函数必有界证明
无穷小比较
α和β存在极限且都是无穷小时:

常见等价无穷小:
求两个无穷小之比的极限时,分子及分母都可用等价无穷小来替代
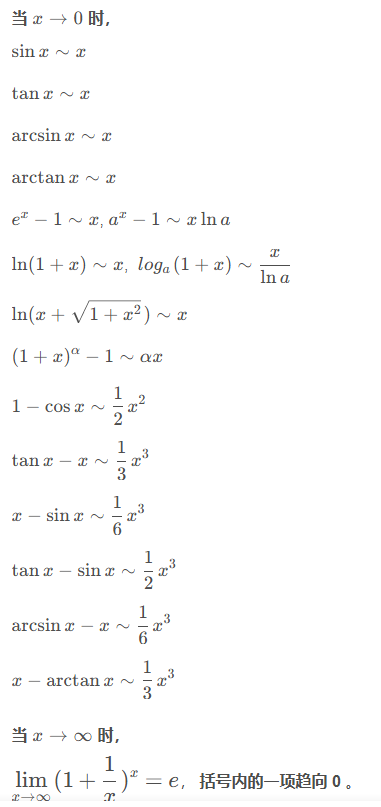
泰勒公式
泰勒公式的作用:用一个多项式函数去逼近一个给定的函数,逼近的时候一定是从函数图像上的某个点展开
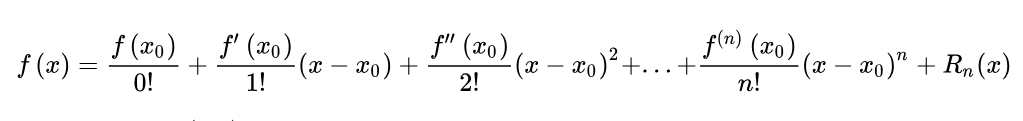
其中Rn(x)表示余项,是泰勒公式与原函数之间的误差
余项的常见形式:
拉格朗日余项
给出了泰勒展开式中误差的精确表达式
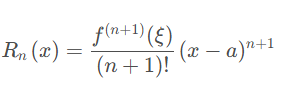
佩亚诺余项
给出了泰勒展开式中误差的一个渐近表达式,描述了误差的一个渐近行为,而不是一个具体的数值
区别
- 拉格朗日余项适用于需要具体误差估计的情况,例如在数值计算中。
- 佩亚诺余项适用于理论分析,特别是在证明某些极限或渐近性质时
常见的泰勒公式

例题
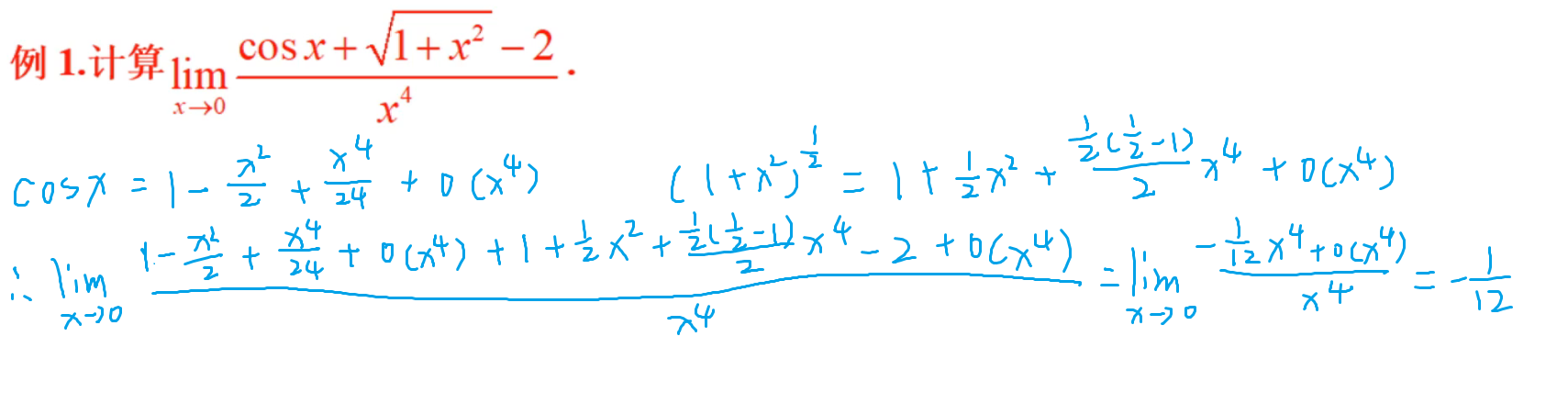



拉格朗日中值定理
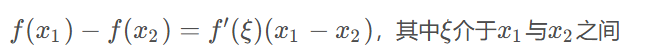
向量代数与空间几何
数量积和向量积
数量积(点乘、是数)
公式:
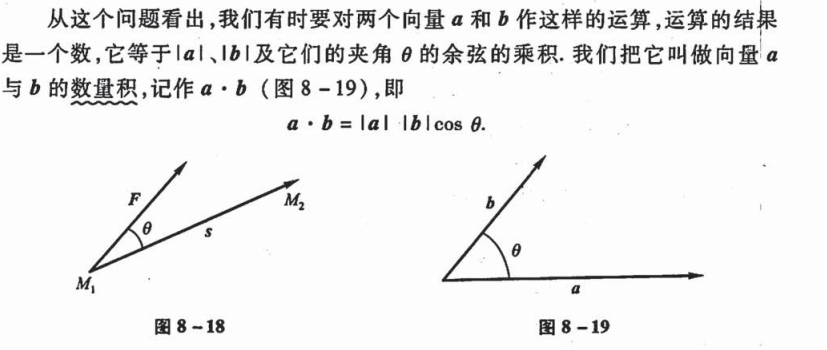

注意点:
- 数量积满足分配律和交换律
- 点乘为0表示a⊥b
向量积(叉乘、是向量)
公式:


注意点:
- 向量积不满足交换律
- 叉乘为0表示a∥b
- 向量积方向垂直于两个向量所在平面
混合积
公式:(a x b) · c,绝对值可表示为六面体的体积
平面
表示平面的方程
点法式:法向量+平面内一点

一般方程
Ax + By + Cz + D = 0

截距式
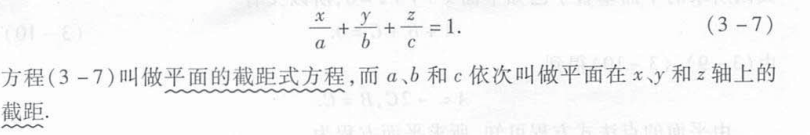
平面夹角

点到平面的距离
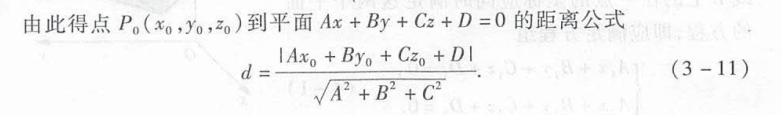
直线
表示直线的方程
一般方程:两个平面的交线
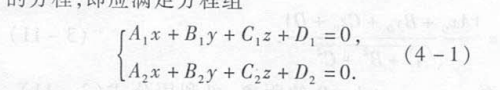
对称式:和方向向量成比例

参数方程

直线夹角

直线与平面的夹角
注意:是直线与平面的夹角,不是直线与法线的夹角

平面束
通过一条直线的所有平面的集合称为平面束
曲面
常见曲面方程
球面
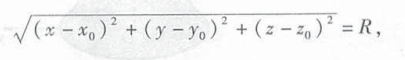
旋转曲面
如一个曲线绕f(0, y, z) = 0绕z轴旋转,则到z轴的距离为 根号(x²+y²) ,方程为f(±根号(x²+y²), z)
绕谁转谁不变
单叶双曲线
xOz面上的双曲线(x²/a² - y²/c²) = 1 绕z轴旋转得到
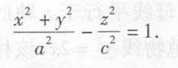
双叶双曲线
xOz面上的双曲线(x²/a² - y²/c²) = 1 绕x轴旋转得到
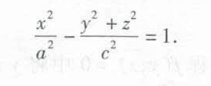
柱面
方程:x² + y² = R²,没有规定z轴,所以z轴为母线,x² + y² = R²为基准线
二次曲面
三元二次方程表示的曲面
椭圆锥面:
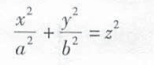
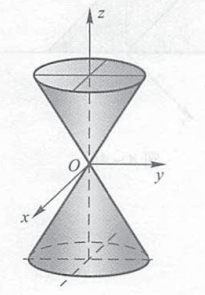
椭球面 :
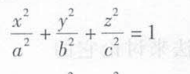
多元函数微分
偏导数
求偏导时将其他变量看做常数
偏导存在,不能保证函数在该点连续
全微分
全增量:各个 变量 都取得增量时 因变量 所获得的增量
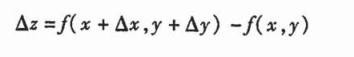
全微分:全增量的近似,全增量 = 全微分 + 高阶无穷小
偏导存在是全微分的 必要不充分条件

全微分等于偏微分之和
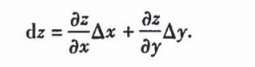
多元复合函数求导
原函数先对复合函数求偏导,复合函数再求偏导

隐函数求导
隐函数:如F(x, f(x))的f(x),F(x,y,f(x,y))的f(x,y)

雅可比式
在方程组的情况下用


几何应用
空间曲线
切向量:
- 参数方程时:求导
- y、z为关于x的方程:x=1,y、z求导
- 两个平面的交线形式:雅可比求出y、z导数,x设为1


曲面
法向量n:
- F(x,y,z)=0:n=(Fx, Fy, Fz)
- z是关于x,y的方程:z移到x、y一边然后求偏导

方向导数与梯度
方向导数:自变量变化时,给定方向的变化率。方向导数是数

梯度:F(x,y)的梯度是(Fx,Fy)。梯度是向量。方向导数=梯度 x 单位向量。二元以上的函数才有梯度
梯度的方向:自变量变化的方向中,使因变量变化率最快的方向
多元函数极值
驻点:一阶偏导为0的点,不一定为极值点
极值点:在某个范围内的极大(极小)值
判断驻点是不是极值点:

偏导不存在的点也有可能是极值点,需要加以判断
条件极值:对自变量有附加条件的极值
求解方法:
- 将条件极值化为无条件极值
- 拉格朗日数乘法

重积分
二重积分定义
常用于算体积

二重积分估值
用于估计二重积分的值的范围

二重积分中值定义

二重积分计算
将二重积分转化为二次积分来计算
要选择合适的坐标系来计算
直角坐标
X型:x轴的积分范围为两个常数
Y型:y轴的积分范围为两个常数
极坐标
适用范围
- 积分区域为圆、圆环、扇形
- f(x²+y²)、f(y/x)、f(x/y)这种不好积分的函数
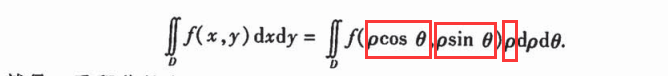
换元法
适用范围
- 被积函数不好积
- 积分区域不好表示

三重积分计算
直角坐标
计算三重积分时,可以先计算一个定积分,再计算一个二重积分
柱面坐标

球面坐标

曲线积分
对弧长的曲线积分
第一类曲线积分
可看做求一段弧的质量(描述标量场对曲线的作用 )

计算
ds的各种表达
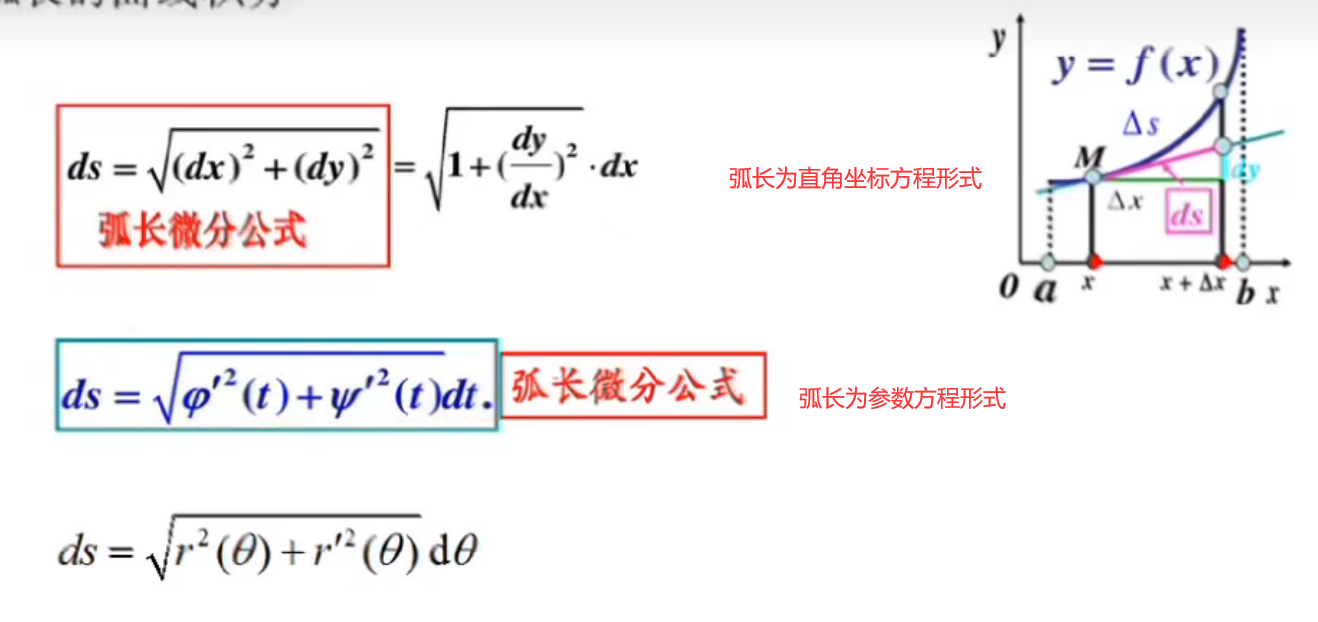
弧长用参数方程表达,如果是算质量,因为质量大于0下限要小于上限

扩展到三维空间
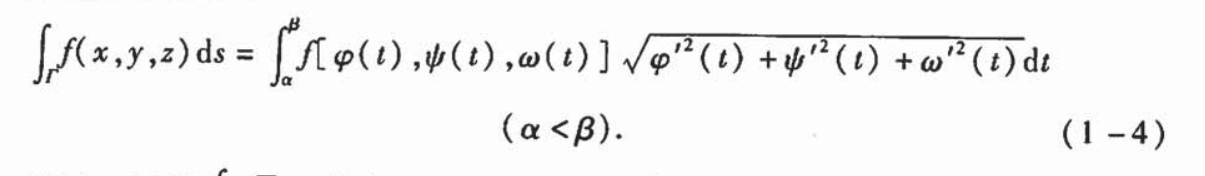
用对称性简化计算

对坐标的曲线积分
第二类曲线积分
可看做变力沿曲线做功(描述向量场对曲线的作用 )

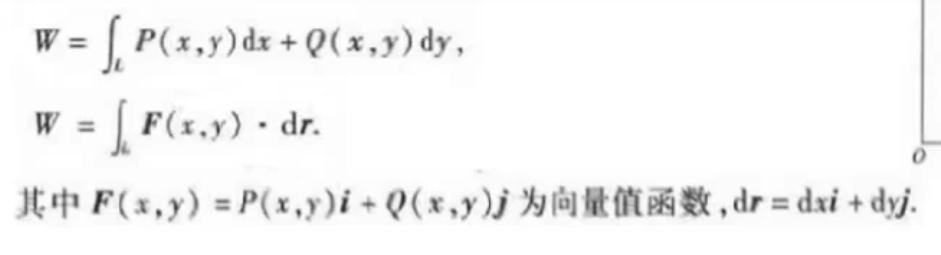
计算
下限不一定小于上限
二维空间

直角坐标下和三维空间下

奇偶性不要乱用,和对弧长的不一样
两类曲线积分的联系
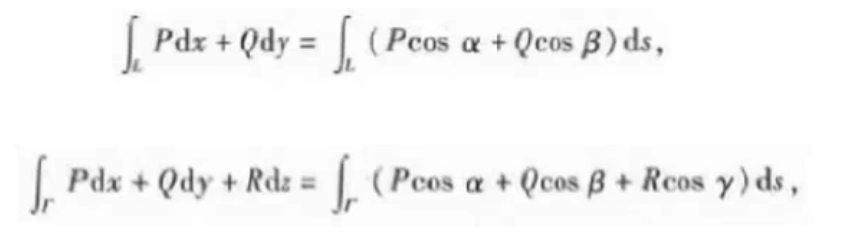
:star:格林公式
平面闭区域上的二重积分与边界曲线的曲线积分的关系

包含奇点的例题

格林公式计算面积
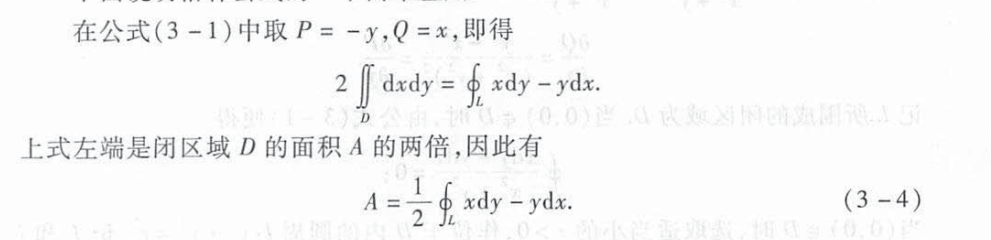
曲线积分与路径无关的条件

:star:斯托克斯公式
格林公式的推广,空间曲面与便捷曲线的曲线积分的关系

斯托克斯公式的其他表达方式

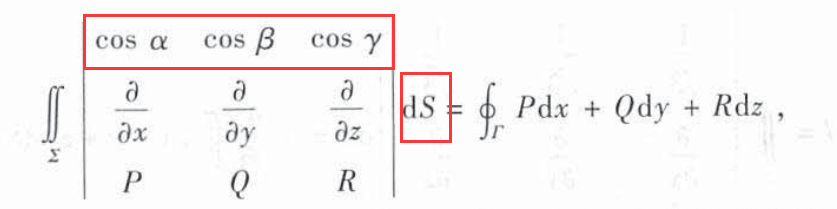
空间曲线与路径无关的条件
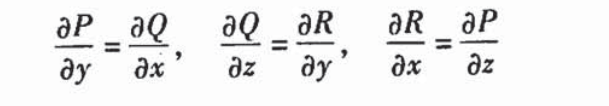
环流量与旋度


曲面积分
对面积的曲面积分
第一类曲面积分
看做计算曲面的质量

计算

对坐标的全面积分
第二类曲面积分
看做通过曲面的流量
法向量n的指向为上侧

:star:计算
化为二重积分:1投2代3定符号

化为第一类曲面积分
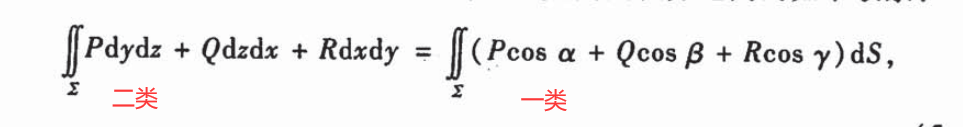
更换投影坐标面

高斯公式

:star:高斯公式

沿闭曲面积分为零的条件

通量和散度